Verschil van kubussenformules, vergelijkingen, voorbeelden, oefeningen

De verschil in blokjes is een binominale algebraïsche uitdrukking van de vorm a³ - b³, waarbij de termen a en b reële getallen of algebraïsche uitdrukkingen van verschillende typen kunnen zijn. Een voorbeeld van een verschil in kubussen is: 8 - x³, aangezien 8 kan worden geschreven als 2³.

Geometrisch kunnen we denken aan een grote kubus, met zijde a, waarvan de kleine kubus met zijde b wordt afgetrokken, zoals geïllustreerd in figuur 1:

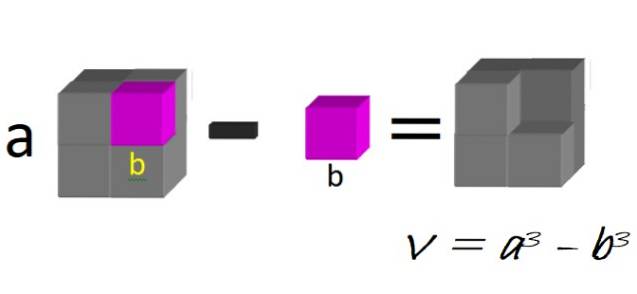
Het volume van de resulterende figuur is precies een verschil in kubussen:

V = een³ - b³

Om een ​​alternatieve uitdrukking te vinden, wordt opgemerkt dat deze figuur kan worden opgesplitst in drie prisma's, zoals hieronder weergegeven:

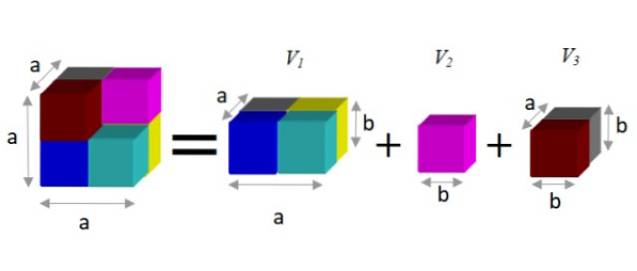
Een prisma heeft een volume dat wordt bepaald door het product van zijn drie dimensies: breedte x hoogte x diepte. Op deze manier is het resulterende volume:

V = een³ - b³ = een^twee.b + b³ + a.b^twee

De factor b het is normaal aan de rechterkant. Bovendien is het in de bovenstaande afbeelding bijzonder waar dat:

b = (a / 2) ⇒ a = b + b

Daarom kan worden gezegd dat: b = a - b. Dus:

naar³ - b³ = b (een^twee + b^twee +a.b) = (a-b) (a^twee + a.b + b^twee​

Deze manier om het verschil in kubussen uit te drukken, zal in veel toepassingen erg nuttig blijken te zijn en zou op dezelfde manier zijn verkregen, zelfs als de zijkant van de ontbrekende kubus in de hoek anders was dan b = a / 2.

Merk op dat het tweede haakjelijkt veel op het opmerkelijke product van het kwadraat van de som, maar de kruisterm wordt niet vermenigvuldigd met 2. De lezer kan de rechterkant ontwikkelen om te verifiëren dat deze daadwerkelijk is verkregen naar³ - b³.

Artikel index

• 1 Voorbeelden
  • 1.1 Factoring van een verschil in kubussen
• 2 Oefening opgelost
  • 2.1 Oefening 1
  • 2.2 Oefening 2
• 3 referenties

Voorbeelden

Er zijn verschillende verschillen in kubussen:

1 - m⁶

naar⁶b³ - 8z¹²Y⁶

(1/125) .x⁶ - 27 en⁹

Laten we ze allemaal eens bekijken. In het eerste voorbeeld kan de 1 worden geschreven als 1 = 1³ en de term m⁶ blijft: (m^twee​³. Beide termen zijn perfecte kubussen, daarom is het verschil:

1 - m⁶ = 1³ - (m^twee​³

In het tweede voorbeeld worden de termen herschreven:

naar⁶b³ = (een^tweeb)³

8z¹²Y⁶ = 2³ (z⁴​³ (Y^twee​³ = (2z⁴Y^twee​³

Het verschil tussen deze kubussen is: (a^tweeb)³ - (2z⁴Y^twee​³.

Ten slotte is de breuk (1/125) (1/5³), x⁶ = (x^twee​³, 27 = 3³ en en⁹ = (en³​³. Als je dit allemaal in de oorspronkelijke uitdrukking vervangt, krijg je:

(1/125) .x⁶  - 27j⁹ = [(1/5) (x^twee​³ - (3j³​³

Factoring van een verschil in kubussen

Door het verschil in kubussen in rekening te brengen, worden veel algebraïsche bewerkingen eenvoudiger. Om dit te doen, volstaat het om de bovenstaande formule te gebruiken:

Nu bestaat de procedure om deze formule toe te passen uit drie stappen:

- Eerst wordt de kubuswortel van elk van de termen van het verschil verkregen.

- Vervolgens worden de binominale en trinominale die aan de rechterkant van de formule verschijnen geconstrueerd.

- Ten slotte worden de binominale en de trinominale plaats vervangen om de definitieve factorisatie te verkrijgen.

Laten we het gebruik van deze stappen illustreren met elk van de voorbeelden van kubusverschillen die hierboven zijn voorgesteld, en zo het gefactureerde equivalent verkrijgen.

voorbeeld 1

Factor de uitdrukking 1 - m⁶   door de beschreven stappen te volgen. We beginnen met het herschrijven van de uitdrukking als 1 - m⁶ = 1³ - (m^twee​³ om de respectievelijke kubuswortels van elke term te extraheren:

Vervolgens worden de binominale en de trinominale constructie geconstrueerd:

a = 1

b = m^twee

Dan:

een - b = 1 - m^twee

 (naar^twee +a.b + b^twee) = 1^twee + 1. m^twee + (m^twee​^twee = 1 + m^twee + m⁴

 Ten slotte wordt het vervangen in de formule a³ - b³ = (a-b) (een^twee +a.b + b^twee​

1 - m⁶ = (1 - m^twee) (1 + m^twee + m⁴​

Voorbeeld 2

Factoriseren:

naar⁶b³ -8z¹²Y⁶ = (een^tweeb)³ - (2z⁴Y^twee​³

Omdat dit perfecte kubussen zijn, zijn de kubuswortels onmiddellijk: a^tweeb en 2z⁴Y^twee, vandaar volgt dat:

- Binominaal: a^tweeb - 2z⁴Y^twee

- Trinominaal: (a^tweeb)^twee + naar^tweeb. 2z⁴Y^twee + (naar^tweeb + 2z⁴Y^twee​^twee

 En nu is de gewenste factorisatie geconstrueerd:

naar⁶b³ -8z¹²Y⁶ = (een^tweeb - 2z⁴Y^twee​[(naar^tweeb)^twee + naar^tweeb. 2z⁴Y^twee + (naar^tweeb + 2z⁴Y^twee​^twee​

= (een^tweeb - 2z⁴Y^twee​[naar⁴b^twee + 2e^tweeb.z⁴Y^twee + (naar^tweeb + 2z⁴Y^twee​^twee​

In principe is de factoring klaar, maar het is vaak nodig om elke term te vereenvoudigen. Vervolgens ontwikkelen we het opmerkelijke product -vierkant van een som- dat aan het einde verschijnt en voegen dan soortgelijke termen toe. Onthoud dat het kwadraat van een som is:

(x + y)^twee = x^twee + 2xy + en^twee

Het opmerkelijke product aan de rechterkant is als volgt ontwikkeld:

(naar^tweeb + 2z⁴Y^twee​^twee = een⁴b^twee + 4e^tweeb.z⁴Y^twee + 4z⁸Y⁴

 Vervanging van de uitbreiding verkregen door de ontbinding van het verschil in kubussen:

naar⁶b³ -8z¹²Y⁶ = (een^tweeb - 2z⁴Y^twee​[naar⁴b^twee + 2e^tweeb.z⁴Y^twee + naar⁴b^twee + 4e^tweeb.z⁴Y^twee + 4z⁸Y⁴​

Als we tenslotte gelijke termen groeperen en de numerieke coëfficiënten in rekening brengen, die allemaal even zijn, krijgen we:

(naar^tweeb - 2z⁴Y^twee​[2a⁴b^twee + 6e^tweeb.z⁴Y^twee + 4z⁸Y⁴] = 2 (een^tweeb - 2z⁴Y^twee​[naar⁴b^twee + 3e^tweeb.z⁴Y^twee + 2z⁸Y⁴​

Voorbeeld 3

Factor (1/125) .x⁶  - 27j⁹ het is veel eenvoudiger dan het vorige geval. Eerst worden de equivalenten van a en b geïdentificeerd:

a = (1/5) x^twee

b = 3j³

Vervolgens worden ze direct vervangen in de formule:

(1/125) .x⁶  - 27j⁹ = [(1/5) x^twee - 3j³​[(1/25) x⁴ + (3/5) x^tweeY³ + 9j⁶​

Oefening opgelost

Het verschil in kubussen heeft, zoals we al zeiden, een verscheidenheid aan toepassingen in Algebra. Laten we eens kijken:

Oefening 1

Los de volgende vergelijkingen op:

een) x⁵ - 125 x^twee = 0

b) 64-729 x³ = 0

Oplossing voor

Eerst wordt de vergelijking op deze manier in rekening gebracht:

X^twee (X³ - 125) = 0

Aangezien 125 een perfecte kubus is, worden de haakjes geschreven als een verschil in kubussen:

X^twee . (X³ - 5³) = 0

De eerste oplossing is x = 0, maar we vinden meer als we x doen³ - 5³ = 0, dan:

X³ = 5³ → x = 5

Oplossing b

De linkerkant van de vergelijking wordt herschreven als 64-729 x³ = 4³ - (9x)³. Daarom:

4³ - (9x)³ = 0

Omdat de exponent hetzelfde is:

9x = 4 → x = 9/4

Oefening 2

Factor de uitdrukking:

(x + y)³ - (x - y)³

Oplossing

Deze uitdrukking is een verschil in kubussen, als we in de factorformule opmerken dat:

een = x + y

b = x- y

Vervolgens wordt eerst de binominale structuur geconstrueerd:

een - b = X + Y - (X- Y) = 2y

En nu de trinominale:

naar^twee + a.b + b^twee = (x + y)^twee + (x + y) (x-y) + (x-y)^twee

Er worden opmerkelijke producten ontwikkeld:

(x + y)^twee = x^twee + 2xy + en^twee

(x + y) (x-y) = x^twee- Y^twee

(x- y)^twee = x^twee - 2xy + en^twee

Vervolgens moet u soortgelijke termen vervangen en verminderen:

naar^twee + a.b + b^twee = x^twee + 2xy + en^twee+ X^twee- Y^twee+ X^twee - 2xy + en^twee = 3x^twee + Y^twee

Factoring resulteert in:

(x + y)³ - (x - y)³ = 2j. (3x^twee + Y^twee​

Referenties

1. Baldor, A. 1974. Algebra. Redactioneel Cultureel Venezolana S.A.
2. Stichting CK-12. Som en verschil van blokjes. Hersteld van: ck12.org.
3. Khan Academy. Factoring van verschillen in kubussen. Hersteld van: es.khanacademy.org.
4. Wiskunde is leuk geavanceerd. Verschil van twee kubussen. Hersteld van: mathsisfun.com
5. UNAM. Factoring van een verschil in kubussen. Hersteld van: dcb.fi-c.unam.mx.