
Euclidische afstandsconcept, formule, berekening, voorbeeld
De Euclidische afstand is een positief getal dat de scheiding aangeeft tussen twee punten in een ruimte waar aan de axioma's en stellingen van de geometrie van Euclides wordt voldaan.
De afstand tussen twee punten A en B in een Euclidische ruimte is de lengte van de vector AB behorend tot de enige lijn die door deze punten loopt.

De ruimte die we waarnemen en waarin wij mensen bewegen, is een driedimensionale ruimte (3-D), waar de axioma's en stellingen van de geometrie van Euclides vervuld zijn. In deze ruimte bevinden zich tweedimensionale deelruimten (vlakken) en eendimensionale deelruimten (lijnen)..
Euclidische ruimtes kunnen eendimensionaal (1-D), tweedimensionaal (2-D), driedimensionaal (3-D) of n-dimensionaal (n-D) zijn.
Punten in de eendimensionale ruimte X zijn die welke behoren tot de georiënteerde lijn (OX), de richting van O naar X is de positieve richting. Om de punten op deze lijn te lokaliseren, wordt het Cartesiaans systeem gebruikt, dat bestaat uit het toekennen van een nummer aan elk punt van de lijn.
Artikel index
- 1 Formule
- 1.1 Euclidische afstand in twee dimensies
- 1.2 Niet-Euclidische oppervlakken
- 1.3 Euclidische afstand in n afmetingen
- 2 Hoe de Euclidische afstand te berekenen
- 3 Voorbeeld
- 4 referenties
Formule
De Euclidische afstand d (A, B) tussen de punten A en B, gelegen op een lijn, wordt gedefinieerd als de vierkantswortel van het kwadraat van de verschillen in hun X-coördinaten:
d (A, B) = √ ((XB - XA) ^ 2)
Deze definitie garandeert dat: de afstand tussen twee punten altijd een positieve grootheid is. En dat de afstand tussen A en B gelijk is aan de afstand tussen B en A.
Figuur 1 toont de eendimensionale Euclidische ruimte gevormd door de lijn (OX) en verschillende punten op die lijn. Elk punt heeft een coördinaat:
Punt A heeft coördinaat XA = 2,5, punt B-coördinaat XB = 4 en punt C-coördinaat XC = -2,5
d (A, B) = √ ((4 - 2,5) 2) = 1,5
d (B, A) = √ ((2,5 - 4) 2) = 1,5
d (A, C) = √ ((- 2,5 - 2,5) 2) = 5,0
Euclidische afstand in twee dimensies
Tweedimensionale Euclidische ruimte is een vlak. De punten van een Euclidisch vlak voldoen aan de axioma's van de meetkunde van Euclides, bijvoorbeeld:
- Een enkele lijn loopt door twee punten.
- Drie punten op het vlak vormen een driehoek waarvan de interne hoeken altijd samen 180º bedragen.
- In een rechthoekige driehoek is het kwadraat van de hypotenusa gelijk aan de som van de kwadraten van zijn benen.
In twee dimensies heeft een punt X- en Y-coördinaten.
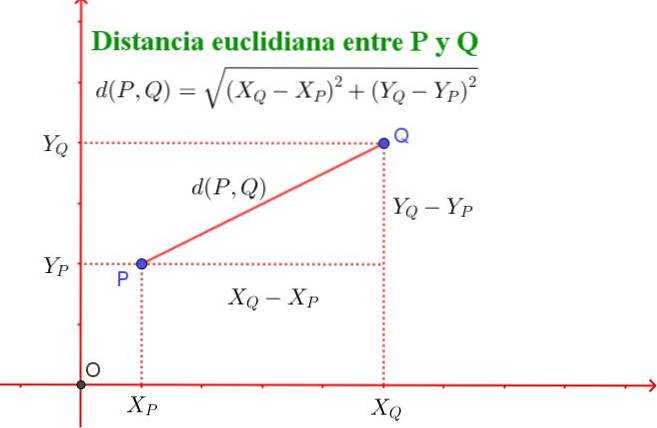
Een punt P heeft bijvoorbeeld coördinaten (XP, YP) en een punt Q-coördinaten (XQ, YQ).
De Euclidische afstand tussen punt P en Q wordt gedefinieerd met de volgende formule:
d (P, Q) = √ ((XQ - XP) ^ 2 + (YQ - YP) ^ 2)
Opgemerkt moet worden dat deze formule equivalent is aan de stelling van Pythagoras, zoals weergegeven in figuur 2.
Niet-Euclidische oppervlakken
Niet alle tweedimensionale ruimtes voldoen aan de Euclidische meetkunde. Het oppervlak van een bol is een tweedimensionale ruimte.
De hoeken van een driehoek op een bolvormig oppervlak tellen niet op tot 180º en daarmee wordt niet voldaan aan de stelling van Pythagoras, daarom voldoet een bolvormig oppervlak niet aan de axioma's van Euclides.
Euclidische afstand in n afmetingen
Het concept van coördinaten kan worden uitgebreid tot grotere dimensies:
- In 2D heeft punt P coördinaten (XP, YP)
- In 3D heeft een punt Q coördinaten (XQ, YQ, ZQ)
- In 4-D heeft punt R coördinaten (XR, YR, ZR, WR)
- In n-D zal een punt P coördinaten hebben (P1, P2, P3, ..., Pn)
De afstand tussen twee punten P en Q in een n-dimensionale Euclidische ruimte wordt berekend met de volgende formule:
d (P, Q) = √ ((Q1 - P1) ^ 2 + (Q2 - P2) ^ 2 +… + (Qn - Pn) ^ 2)
De meetkundige plaats van alle punten Q in een n-dimensionale Euclidische ruimte op gelijke afstand van een ander vast punt P (het midden) vormt een n-dimensionale hypersphere.
Hoe de Euclidische afstand te berekenen
Het volgende laat zien hoe de afstand tussen twee punten in de Euclidische driedimensionale ruimte wordt berekend.
Stel dat punt A van cartesische coördinaten x, y, z gegeven door A :( 2, 3, 1) en punt B van coördinaten B :( -3, 2, 2).
We willen de afstand tussen deze punten bepalen, waarbij gebruik wordt gemaakt van de algemene relatie:
d (A, B) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )
d (A, B) = √ (25 + 1 + 1) = √ (27) = √ (9 * 3) = 3 √ (3) = 5.196
Voorbeeld
Er zijn twee punten P en Q. Het punt P van de cartesische coördinaten x, y, z gegeven door P :( 2, 3, 1) en het punt Q van de coördinaten Q :( -3, 2, 1).
Er wordt gevraagd om de coördinaten te vinden van het middelpunt M van het segment [PQ] dat de twee punten met elkaar verbindt.
Oplossing:
Aangenomen wordt dat het onbekende punt M coördinaten heeft (X, Y, Z).
Aangezien M het middelpunt van [PQ] is, moet het waar zijn dat d (P, M) = d (Q, M), dus d (P, M) ^ 2 = d (Q, M) ^ 2 moet ook waar zijn :
(X - 2) ^ 2 + (Y - 3) ^ 2 + (Z - 1) ^ 2 = (X - (-3)) ^ 2 + (Y - 2) ^ 2 + (Z - 1) ^ 2
Omdat in dit geval de derde term in beide leden gelijk is, vereenvoudigt de vorige uitdrukking tot:
(X - 2) ^ 2 + (Y - 3) ^ 2 = (X + 3) ^ 2 + (Y - 2) ^ 2
We hebben dan een vergelijking met twee onbekenden X en Y. Een andere vergelijking is nodig om het probleem op te lossen.
Punt M behoort tot de lijn die door de punten P en Q loopt, die we als volgt kunnen berekenen:
De eerste is de regisseur-vector PQ van het rechte stuk: PQ < -3-2, 2-3, 1-1> < -5, -1, 0 >.
Later P.M OP + naar PQ, waar OP is de positievector van punt P en naar is een parameter die bij de reële getallen hoort.
De bovenstaande vergelijking staat bekend als de vectorvergelijking van de lijn, die in cartesiaanse coördinaten de volgende vorm aanneemt:
< X-2, Y-3, Z-1> <2, 3, 1> + naar < -5, -1, 0> < 2 - 5a, 3 - a, 0>
Vergelijking van de overeenkomstige componenten die we hebben:
X - 2 = 2-5 a; Y - 3 = 3 -a; Z - 1 = 0
Dat wil zeggen, X = 4 - 5a, Y = 6 - a, uiteindelijk Z = 1.
Het wordt vervangen in de kwadratische uitdrukking die X relateert aan Y:
(4 - 5a - 2) ^ 2 + (6 - a - 3) ^ 2 = (4 - 5a + 3) ^ 2 + (6 - a - 2) ^ 2
Het is vereenvoudigd:
(2 - 5a) ^ 2 + (3 -a) ^ 2 = (7 - 5a) ^ 2 + (4 - a) ^ 2
Ontvouwt zich nu:
4 + 25 a ^ 2 - 20a + 9 + a ^ 2 - 6a = 49 + 25 a ^ 2 - 70a + 16 + a ^ 2 - 8a
Het is vereenvoudigd en annuleert dezelfde voorwaarden in beide leden:
4 - 20a + 9 - 6a = 49 - 70a + 16 - 8a
De parameter a wordt gewist:
52 a = 49 + 16 - 4 - 9 = 52 resulterend in dat a = 1.
Dat wil zeggen, X = 4 - 5, Y = 6 - 1, tenslotte Z = 1.
Ten slotte krijgen we de Cartesiaanse coördinaten van het middelpunt M van het segment [PQ]:
M: (-1, 5, 1).
Referenties
- Lehmann C. (1972) Analytische meetkunde. UTEHA.
- Superprof. Afstand tussen twee punten. Hersteld van: superprof.es
- UNAM. Afstand tussen affiene sublineaire spruitstukken. Hersteld van: prometeo.matem.unam.mx/
- Wikipedia. Euclidische afstand. Hersteld van: es.wikipedia.com
- Wikipedia. Euclidische ruimte. Hersteld van: es.wikipedia.com


Niemand heeft nog op dit artikel gereageerd.