
Spanningstest hoe het wordt gedaan, eigenschappen, voorbeelden

EEN stresstest Het is een experimentele test die wordt uitgevoerd op een materiaalmonster om te bepalen hoe goed het bestand is tegen trekspanningen. Dankzij dit is het mogelijk om veel van de mechanische eigenschappen van het materiaal te kennen en te bepalen of het geschikt is voor een bepaald ontwerp..
Het monster wordt meestal een cilinder genoemd reageerbuis. Hierop wordt een spanning uitgeoefend, bestaande uit het uitoefenen van twee tegengestelde krachten aan de uiteinden die de staaf strekken en vervormen. De test gaat door met toenemende inspanningen, totdat het preparaat uiteindelijk breekt.

Let op de grootte van de krachten en de vervorming die ze in het preparaat veroorzaken, van kleine krachten die geen permanente vervorming veroorzaken, tot de spanning die ervoor zorgt dat het onderdeel breekt..
Daar eindigt de gegevensverzameling en wordt een spanning-rekgrafiek opgesteld, die zal dienen om het gedrag van materialen zoals metalen, keramiek, cement, hout en polymeren te analyseren..
Artikel index
- 1 Wat wordt er gebruikt voor het trekproefexperiment?
- 2 Eigenschappen en gegevens verkregen
- 2.1 Elastische zone
- 2.2 Kunststof zone
- 3 Voorbeelden van trekproeven
- 3.1 Brosse en ductiele materialen
- 3.2 Reactie van verschillende materialen op de stresstest
- 4 referenties
Wat wordt gebruikt voor het trekproefexperiment?
Het experiment wordt gedaan met behulp van speciale machines zoals die in figuur 1, die de nodige inspanning leveren om het materiaal te laden en vervolgens te lossen om de vervorming te evalueren..
Wat het monster betreft, het is een buis met een constante doorsnede, cilindrisch, rechthoekig of vierkant, waarvan de afmetingen gestandaardiseerd zijn. De uiteinden zijn breder om het vastklemmen aan de monsterhouder te vergemakkelijken, zoals te zien in figuur 2 links.
De aanvankelijke lengte Lof Het gekalibreerde gebied wordt gemeten en gemarkeerd op de reageerbuis. Het wordt vervolgens op de testmachine geklemd en de testmachine begint..

Eigenschappen en gegevens verkregen
Materialen hebben verschillende gedragingen onder spanning, zoals weergegeven in de volgende grafiek waarvoor staal werd gebruikt. De krachten die op de verticale as worden uitgeoefend, worden aangeduid met de Griekse letter σ en de rek op de horizontale as, ε genaamd.
Stam heeft geen afmetingen, aangezien het het quotiënt is tussen de lengteverandering van het monster ΔL = LF. - L.of en de aanvankelijke lengte. A) Ja:
ε = ΔL / Lof
Van zijn kant is de grootte van de spanning σ de verhouding kracht / dwarsdoorsnede.
In de grafiek worden twee belangrijke gebieden onderscheiden: elastische zone en plastische zone.
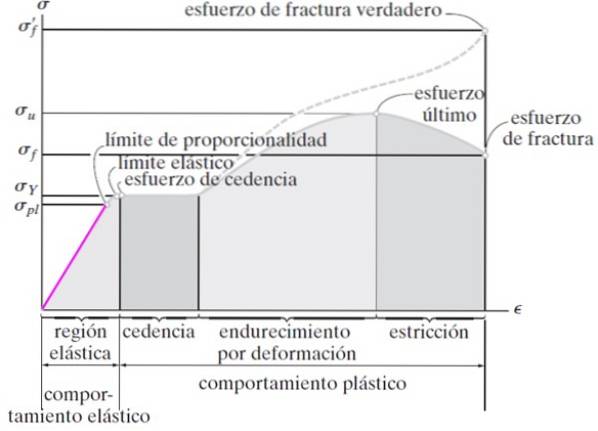
Elastische zone
Wanneer de trekspanning σ klein is, is de vervorming proportioneel, wat bekend staat als de wet van Hooke:
σ = Y ε
Zodra de inspanning stopt, keert het lichaam terug naar zijn oorspronkelijke afmetingen. Dit is het elastische gebied in kleur in figuur 3, dat zich uitstrekt tot het punt dat wordt genoemd evenredigheidsgrens. Tot daar gehoorzaamt het materiaal de wet van Hooke.
De evenredigheidsconstante Y is de Young's modulus, karakteristiek voor het materiaal en die kunnen worden bepaald uit trek- en druktests.
Young's modulus heeft drukeenheden, in het internationale systeem [Y] = N / m ^ 2 = Pa. Spanning, zoals reeds vermeld, is dimensieloos, daarom heeft de spanning σ ook afmetingen van kracht als gevolg van de eenheid van de dwarsdoorsnede en in SI is zijn eenheid de pascal: [σ] = N / m ^ 2 = Pa.
Van de limiet van evenredigheid en toenemende spanning, gaat men vooruit in een gebied waar de vervorming omkeerbaar is, maar niet gehoorzaamt aan de wet van Hooke. Het eindigt op het punt van waaruit het lichaam permanent wordt vervormd, genaamd elastische limiet.
Kunststof zone
Het materiaal komt dan in het gebied van plastisch gedrag. Zodra de elastische gedragszone wordt overschreden, komt het staal het gebied van de Het leveren van inspanning of kruip, waarbij het monster vervormt maar niet breekt, hoewel de spanning constant blijft op σY.
Zodra de vloeigrens wordt overschreden, neemt de vervorming toe met de aangebrachte spanning, maar niet langer op een lineaire manier..
Het materiaal ondergaat veranderingen op moleculair niveau en spanningsharding treedt op. Daarom zien we dat er steeds meer inspanningen nodig zijn om tot een vervorming te komen.
De limiet van deze zone is in de laatste poging. Het materiaal wordt op dit punt als gebroken beschouwd, hoewel het exemplaar nog heel is. Van daaruit wordt de belasting die nodig is om vervorming te produceren verminderd en wordt het monster geleidelijk dunner (strictuur) totdat het uiteindelijk breekt (figuur 2, rechts).
Deze curve en zijn regio's worden conventionele breukspanning genoemd. Maar daarboven is een stippellijn, genaamd echte breukspanning, die wordt verkregen door de momentane of ware lengte van het specimen te registreren, in plaats van te werken met de oorspronkelijke lengte om de rek te vinden, zoals uitgelegd aan het begin.
Beide krommen, de echte en de conventionele, vallen samen in de zone van kleine inspanningen tot de zone van opbrengst. In ieder geval is voorzien dat het materiaal in het elastische bereik werkt om permanente vervormingen te vermijden die de goede werking van het vervaardigde onderdeel verhinderen..
Een van de belangrijkste gegevens die uit de test zijn verkregen, is dus de spanning σY die de elastische limiet definieert.
Voorbeelden van trekproeven
Het materiaal dat in de bovenstaande beschrijving als model is gebruikt, is staal, dat veel wordt gebruikt in de bouw en de industrie. Maar er zijn veel materialen zoals beton, beton, diverse metalen, legeringen en hout, die ook veel gebruikt worden..
Elk heeft een karakteristieke spanning-rekcurve, en volgens zijn reactie op spanning of tractie, worden ze ingedeeld in twee categorieën: bros of taai..
Broze en taaie materialen
In de volgende grafiek σ versus ε (stress-spanning) broze materialen worden vergeleken (bros) en ductiel (ductiel), hoewel het nodig is om duidelijk te maken dat hetzelfde materiaal de ene of de andere respons kan hebben, afhankelijk van factoren zoals temperatuur. Materialen hebben de neiging bros te zijn bij lage temperaturen.
Het opmerkelijke verschil tussen de twee is dat bros materiaal geen of een zeer klein opbrengstgebied heeft. Zodra de elastische limiet wordt overschreden, breekt het preparaat. Aan de andere kant absorberen ductiele materialen meer energie voordat ze breken, omdat ze een grote plastic zone hebben.
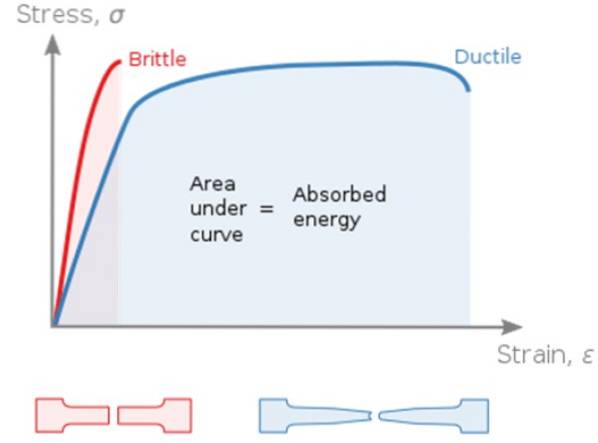
De stresstest is nuttig om het materiaal te classificeren, waarbij de voorkeur wordt gegeven aan het gebruik van ductiele materialen, aangezien ze meer energie absorberen en lang voordat ze breken in staat zijn om te vervormen..
Er moet ook worden opgemerkt dat hoewel sommige materialen broos zijn onder spanning, ze andere spanningen beter kunnen weerstaan, zoals we hieronder zullen zien..
Reactie van verschillende materialen op stresstest
-Grijs gietijzer: broos in spanning, sterker in compressie.
-Bronzen: ductiel.
-Beton: kwetsbaar afhankelijk van het type mengsel, maar zeer goed bestand tegen compressie. Als het onder spanning komt te staan, moet het worden verstevigd door middel van stalen staven.
-Hout: afhankelijk van de oorsprong is het matig taai.
-Staal: broos bij een hoog koolstofgehalte.
-Methacrylaat: ductiel met stijgende temperatuur.
Referenties
- Beer, F. 2010. Mechanica van materialen. McGraw Hill. 5e. Editie.
- Cavazos, J.L. Materiaalmechanica. Hersteld van: youtube.com.
- Hibbeler, R. 2011. Mechanica van materialen. Achtste editie. Pearson.
- Collins, D. Lineaire bewegingstips. Mechanische eigenschappen van materialen: spanning en rek. Hersteld van: linearmotiontips.com.
- Valera Negrete, J. 2005. Opmerkingen over algemene fysica. UNAM.
- Wikipedia. Trektest. Hersteld van: es.wikipedia.org.



Niemand heeft nog op dit artikel gereageerd.