
Translationele evenwichtscondities, voorbeelden, oefeningen
Er wordt beweerd dat er een object in zit translationeel evenwicht wanneer de som van de krachten die erop inwerken nul is. Dit betekent niet dat er noodzakelijkerwijs rust is, maar de beweging, als deze bestaat, zou uniform rechtlijnig zijn of uitsluitend roterend, in het geval van een groot object..
De voorwaarden van mechanisch evenwicht zijn gebaseerd op de wetten van de mechanica van Newton. Inderdaad, de eerste wet vertelt ons dat een object in rust is of beweegt met een uniforme rechtlijnige beweging MRU, op voorwaarde dat er geen netto kracht op inwerkt.

Nu is de netto kracht of resulterende kracht gewoon de vectorsom van alle krachten die op het object inwerken. Volgens de tweede wet van Newton moet deze som gelijk zijn aan het product tussen de massa en de versnelling, maar als het object niet wordt versneld, verdwijnt deze som.
En als er geen versnelling is, zijn er de twee bovengenoemde mogelijkheden: het lichaam is in rust, dat wil zeggen, het beweegt niet, of als dat wel het geval is, moet het met MRU zijn. In het eerste geval spreken we van statisch transnationaal evenwicht en in het tweede geval van dynamisch.
Translationeel evenwicht is een belangrijke factor in veel aspecten van engineering, bijvoorbeeld in de constructie. De elementen waaruit een gebouw bestaat: balken, kabels, frames en meer, moeten in balans zijn om de stabiliteit van de behuizing te garanderen.
Translationeel evenwicht wordt ook gezocht bij mobiele constructies, zoals roltrappen, transportbanden en bij de beoefening van talrijke sporten..
Artikel index
- 1 Toestand van translationeel evenwicht
- 1.1 Free-body-diagrammen
- 2 Voorbeelden van translationeel evenwicht
- 2.1 Gebouwen en wegen
- 2.2 Boeken en voorwerpen op planken
- 2.3 Het meubilair
- 2.4 Verkeerslichten
- 2.5 Openbare verlichting
- 3 Oefening opgelost
- 3.1 Oplossing
- 4 referenties
Translationele evenwichtstoestand
Stel dat er meerdere krachten op een lichaam werken, dat noemen we F.1, F.twee, F.3 . F.n, vetgedrukt gebruiken om het feit te benadrukken dat krachten vectoren zijn en als zodanig moeten worden toegevoegd.
De vectorsom van al deze krachten wordt genoemd resulterende kracht of netto kracht. Als deze optelling resulteert in de nulvector, is aan de voorwaarde voor het translationeel evenwicht voldaan:
F.1+ F.twee+ F.3 .+ F.n 0
Deze voorwaarde kan compact worden geschreven met behulp van sommatie-notatie:
F.ik 0
In termen van de componenten van de resulterende kracht, kan de bovenstaande vergelijking, die vector is, worden opgesplitst in drie scalaire vergelijkingen, één voor elke component van de resulterende kracht:
∑ F.ix = 0; ∑ F.Y = 0 en ∑ Fz = 0
In de praktijk is het niet eenvoudig om de som van krachten op te heffen, omdat wrijving een contactkracht tussen oppervlakken is die door een andere kracht nauwelijks volledig wordt opgeheven..
Dit is de reden dat echte objecten bijna nooit zijn vrijgesteld van externe krachten, en als gevolg daarvan is het moeilijk om translationeel evenwicht te verkrijgen.
Daarom gebruiken ingenieurs mechanismen om wrijving te verminderen, zoals lagers en het gebruik van smeeroliën..
Free-body-diagrammen
Het free-body-diagram is een diagram waarin de krachten die op het lichaam werken, worden getekend. Bij het zoeken naar translationeel evenwicht moeten deze krachten in evenwicht zijn. Als bijvoorbeeld een naar beneden gerichte verticale kracht werkt, zoals een gewicht, dan moet er een opwaartse verticale kracht zijn die exact dezelfde grootte heeft.
Deze kracht kan worden geleverd door de hand die het object ondersteunt zodat het niet valt, een touw of gewoon het oppervlak van een tafel.
Als er een kracht is die raakt aan het oppervlak, zoals kinetische of statische wrijving, moet er een andere tegenkracht zijn om het evenwicht te laten bestaan. Laten we bijvoorbeeld eens kijken naar het gewicht dat aan de snaren hangt die in de volgende afbeelding worden getoond.
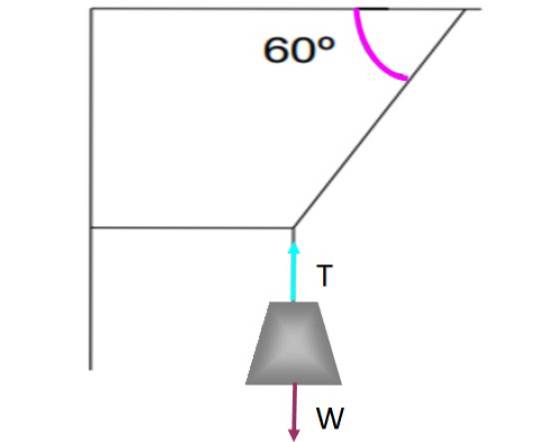
Het gewicht wordt in translatiebalans gehouden en zonder te bewegen, dankzij het verticale touw dat het vasthoudt door een spanning uit te oefenen T dat compenseert het gewicht W.. Elke kracht is op het gewicht weergegeven door een pijl, elk van gelijke grootte en met dezelfde richting, maar in tegengestelde richting..
De evenwichtskracht
Stel dat een reeks krachten op een object inwerkt. Dit heet een krachtsysteem waaruit de resultante kan worden gevonden, zoals hierboven uitgelegd: door elk van de krachten van het systeem vectorachtig bij elkaar op te tellen.
Welnu, de kracht die tegengesteld is aan deze resultante wordt genoemd evenwichtskracht. Als de resulterende kracht is F.R en de balancerende kracht is EN, dan:
EN + F.R = 0
Daarom:
EN - F.R
Voorbeelden van translationeel evenwicht
Veel objecten die we dagelijks vinden, binnen en buiten het huis, verkeren in translationeel evenwicht:
Gebouwen en wegen
Gebouwen en wegen zijn zo gebouwd dat ze stabiel blijven en niet omvallen of instorten. In wolkenkrabbers en in het algemeen zeer hoge gebouwen is echter enige flexibiliteit nodig om de werking van de wind te weerstaan..
Boeken en voorwerpen op planken
Boeken in een bibliotheek en producten in de winkelrekken zijn objecten die in translationeel evenwicht blijven en niet bewegen..
De meubels
Het meubilair, de flatscreen-tv en de schilderijen aan de muur, evenals de lampen die aan het plafond hangen, om maar een paar objecten te noemen, zijn in translationeel evenwicht..
Verkeerslichten
De verkeerslichten zijn bevestigd met palen en kabels, zodat ze niet vallen. Toch weten we dat de wind ze laat zwaaien.
Openbare verlichting
De straatlantaarns zijn ook in translatiebalans, gefixeerd op de lantaarnpalen, zoals de straatlantaarn in de hoofdafbeelding..
Oefening opgelost
Hoe groot moet de kracht zijn F.s van statische wrijving zodat de doos in de figuur stil blijft staan in het midden van het hellende vlak onder een hoek α van 37º? De massa van de doos is m = 8 kg.
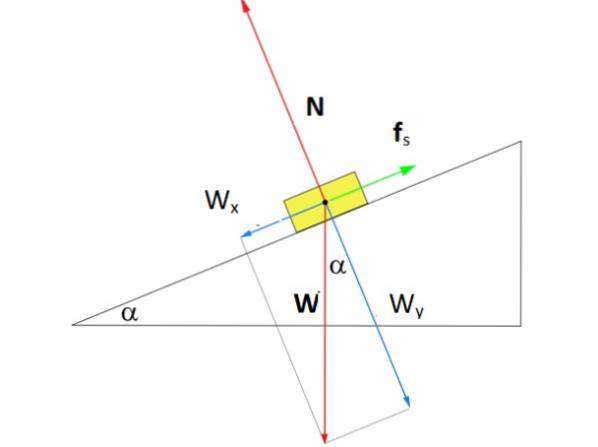
Oplossing
De figuur toont het vrije lichaam diagram van de doos in het vliegtuig. Er werken drie krachten op: gewicht W., verticaal naar beneden gericht, de normale N, dat is de loodrechte kracht die wordt uitgeoefend door het oppervlak van het vlak op de doos, en tenslotte de statische wrijvingskracht F.s dat is in tegenstelling tot de doos die naar beneden glijdt.
De translationele evenwichtstoestand stelt dat:
W. + N + F.s 0
Maar we moeten niet vergeten dat dit een vectorsom is en om het uit te voeren is het nodig om de krachten te ontleden in componenten langs de coördinaatassen.
In de figuur is een coördinatensysteem getekend waarbij de x-as evenwijdig loopt aan het oppervlak van het hellende vlak. Bij deze keuze valt de statische wrijving op die as, terwijl de normaal op de y-as ligt. Gewicht is de enige kracht die geneigd is en moet worden afgebroken met behulp van trigonometrie:
W.X = W. sin α
W.Y = W. cos α
De som van de krachten langs elke as is:
∑ F.Y = N - WY = 0
∑ F.X = fs - W.X = 0
Uit deze laatste vergelijking volgt dat:
F.s = WX
En zoals WX = W. sin α en de grootte van het gewicht is op zijn beurt W = m.g, waar g de waarde van de zwaartekracht is, dan is de grootte van de statische wrijving eenvoudig:
F.s = m⋅g⋅sen α = 8 kg × 9,8 m / stwee × sin 37º = 47,2 N.
Referenties
- Bauer, W. 2011. Physics for Engineering and Sciences. Deel 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 2. Dynamiek. Bewerkt door Douglas Figueroa (USB).
- Giambattista, A. 2010. Physics. 2e. Ed McGraw Hill.
- Serway, R., Jewett, J. (2008). Physics for Science and Engineering. Deel 1. 7ma. Ed. Cengage Learning.
- Tippens, P. 2011. Fysica: concepten en toepassingen. 7e editie. Mcgraw heuvel.


Niemand heeft nog op dit artikel gereageerd.