
Bemonsteringsfoutformules en vergelijkingen, berekeningen, voorbeelden
De bemonsteringsfout of voorbeeldfout In statistieken is het het verschil tussen de gemiddelde waarde van een steekproef en de gemiddelde waarde van de totale populatie. Om het idee te illustreren, stellen we ons voor dat de totale bevolking van een stad één miljoen mensen is, waarvan de gemiddelde schoenmaat gewenst is, waarvoor een willekeurige steekproef van duizend mensen wordt genomen..
De gemiddelde grootte die uit de steekproef naar voren komt, zal niet noodzakelijk samenvallen met die van de totale populatie, maar als de steekproef niet vertekend is, moet de waarde dichtbij zijn. Dit verschil tussen de gemiddelde waarde van de steekproef en die van de totale populatie is de steekproeffout.
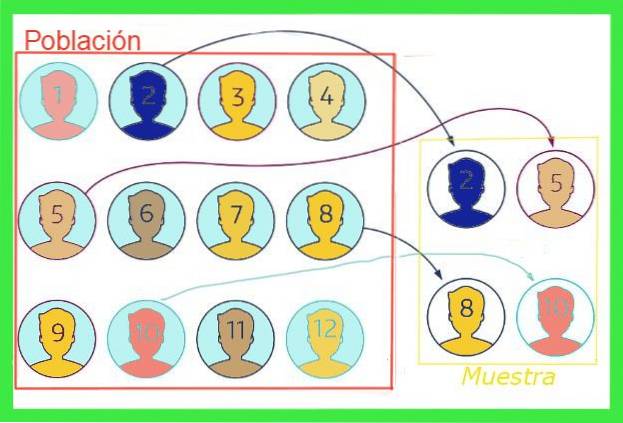
Over het algemeen is de gemiddelde waarde van de totale populatie onbekend, maar er zijn technieken om deze fout te verminderen en formules om de steekproeffoutmarge dat zal in dit artikel worden onthuld.
Artikel index
- 1 Formules en vergelijkingen
- 2 Hoe de steekproeffout te berekenen
- 2.1 Voor een betrouwbaarheidsniveau γ
- 3 voorbeelden
- 3.1 - Voorbeeld 1
- 3.2 - Voorbeeld 2
- 3.3 - Voorbeeld 3
- 3.4 - Voorbeeld 4
- 3.5 - Oefening 5
- 4 referenties
Formules en vergelijkingen
Stel dat u de gemiddelde waarde van een bepaald meetbaar kenmerk wilt weten X in een populatie van grootte N, maar hoe N is een groot aantal, is het niet haalbaar om de studie over de totale populatie uit te voeren, dan gaan we verder met het nemen van een aleatory monster van grootte n<
De gemiddelde waarde van het monster wordt aangegeven door
Stel dat ze nemen m steekproeven van de totale populatie N, allemaal even groot n met gemiddelde waarden
Deze gemiddelde waarden zullen niet identiek zijn aan elkaar en zullen allemaal rond de gemiddelde populatiewaarde liggen μ. De marge van steekproeffout E geeft de verwachte scheiding van de gemiddelde waarden aan
De standaard foutmarge ε grootte steekproef n het is:
ε = σ / √n
waar σ is de standaarddeviatie (de vierkantswortel van de variantie), die wordt berekend met behulp van de volgende formule:
σ = √ [(x -
De betekenis van standaard foutmarge ε is de volgende:
De middelste waarde
Hoe de steekproeffout te berekenen
In het vorige gedeelte werd de formule gegeven om de fout bereik standaard- van een steekproef van grootte n, waarbij het woord standaard aangeeft dat het een foutmarge is met een betrouwbaarheid van 68%.
Dit geeft aan dat als er veel monsters van dezelfde grootte zijn genomen n, 68% van hen geeft gemiddelde waarden
Er is een eenvoudige regel, de regel 68-95-99.7 waarmee we de marge van kunnen vinden bemonsteringsfout E voor betrouwbaarheidsniveaus van 68%, 95% Y 99,7% gemakkelijk, aangezien deze marge 1 ⋅ isε, 2⋅ε en 3⋅ε respectievelijk.
Voor een zeker niveau van vertrouwen γ
Als hij betrouwbaarheidsniveau γ niet een van de bovenstaande is, dan is de steekproeffout de standaarddeviatie σ vermenigvuldigd met de factor Zγ, die wordt verkregen via de volgende procedure:
1. - Ten eerste de significantieniveau α die wordt berekend uit betrouwbaarheidsniveau γ met behulp van de volgende relatie: α = 1 - γ
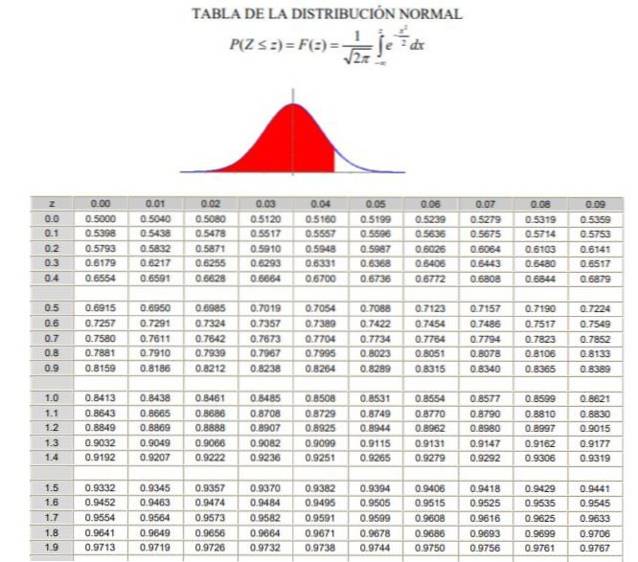
2.- Vervolgens moet u de waarde 1 berekenen - α / 2 = (1 + γ) / 2, wat overeenkomt met de geaccumuleerde normale frequentie tussen -∞ en Zγ, in een normale of gestandaardiseerde Gauss-verdeling F (z), waarvan de definitie te zien is in figuur 2.
3.- De vergelijking is opgelost F (Zγ) = 1 - α / 2 door middel van de tabellen van de normale verdeling (cumulatief) F., of door middel van een computertoepassing die de omgekeerde gestandaardiseerde Gauss-functie heeft F.-1.
In het laatste geval hebben we:
Zγ = G-1(1 - α / 2).
4.- Tenslotte wordt deze formule toegepast voor de steekproeffout met betrouwbaarheidsniveau γ:
E = Zγ(σ / √n)
Voorbeelden
- voorbeeld 1
Bereken de standaard foutmarge in het gemiddelde gewicht van een steekproef van 100 pasgeborenen. De berekening van het gemiddelde gewicht was
Oplossing
De standaard foutmarge het is ε = σ / √n = (1.500 kg) / √100 = 0,15 kg. Wat betekent dat uit deze gegevens kan worden afgeleid dat het gewicht van 68% van de pasgeborenen tussen 2.950 kg en 3,25 kg ligt.
- Voorbeeld 2
Bepalen de marge van steekproeffout E en het gewichtsbereik van 100 pasgeborenen met een betrouwbaarheidsniveau van 95% als het gemiddelde gewicht 3100 kg is met standaarddeviatie σ = 1.500 kg.
Oplossing
Als het regel 68; 95; 99,7 → 1⋅ε; 2⋅ε3⋅ε, jij hebt:
E = 2⋅ε = 2⋅0,15 kg = 0,30 kg
Dat wil zeggen, 95% van de pasgeborenen zal een gewicht hebben tussen 2.800 kg en 3.400 kg.
- Voorbeeld 3
Bepaal het gewichtsbereik van de pasgeborenen uit Voorbeeld 1 met een betrouwbaarheidsmarge van 99,7%.
Oplossing
De steekproeffout met 99,7% betrouwbaarheid is 3 σ / √n, wat voor ons voorbeeld E = 3 * 0,15 kg = 0,45 kg is. Hieruit wordt geconcludeerd dat 99,7% van de pasgeborenen een gewicht tussen 2.650 kg en 3.550 kg zal hebben.
- Voorbeeld 4
Bepaal de factor Zγ voor een betrouwbaarheidsniveau van 75%. Bepaal de marge van de steekproeffout met dit betrouwbaarheidsniveau voor het geval gepresenteerd in voorbeeld 1.
Oplossing
De betrouwbaarheidsniveau het is γ = 75% = 0,75 die gerelateerd is aan de mate van belangrijkheid α door relatie γ= (1 - α), zodat het significantieniveau α = 1 - 0,75 = 0,25.
Dit betekent dat de cumulatieve normale kans tussen -∞ en Zγ het is:
P (Z ≤ Zγ ) = 1 - 0,125 = 0,875
Wat overeenkomt met een waarde Zγ 1.1503, zoals weergegeven in figuur 3.
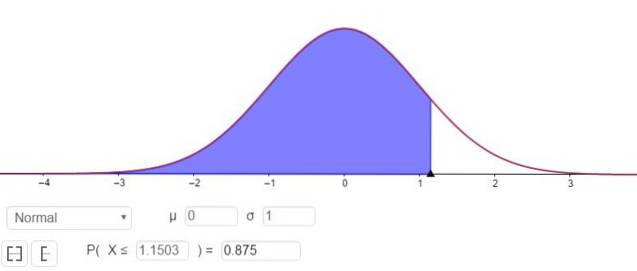
Dat wil zeggen, de steekproeffout is E = Zγ(σ / √n) 1.15(σ / √n).
Toegepast op de gegevens uit voorbeeld 1, geeft het een foutmelding van:
E = 1,15 * 0,15 kg = 0,17 kg
Met een betrouwbaarheidsniveau van 75%.
- Oefening 5
Wat is het betrouwbaarheidsniveau als Zα / 2 = 2,4 ?
Oplossing
P (Z ≤ Zα / 2 ) = 1 - α / 2
P (Z ≤ 2,4) = 1 - α / 2 = 0,9918 → α / 2 = 1 - 0,9918 = 0,0082 → α = 0,0164
Het significantieniveau is:
α = 0,0164 = 1,64%
En tot slot blijft het betrouwbaarheidsniveau:
1- α = 1 - 0,0164 = 100% - 1,64% = 98,36%
Referenties
- Canavos, G. 1988. Waarschijnlijkheid en statistiek: toepassingen en methoden. Mcgraw heuvel.
- Devore, J. 2012. Waarschijnlijkheid en statistiek voor techniek en wetenschap. 8e. Editie. Cengage.
- Levin, R. 1988. Statistieken voor beheerders. 2e. Editie. Prentice hal.
- Sudman, S. 1982. Vragen stellen: een praktische gids voor het ontwerpen van vragenlijsten. San Francisco. Jossey bas.
- Walpole, R. 2007. Waarschijnlijkheid en statistiek voor techniek en wetenschappen. Pearson.
- Wonnacott, T.H. en R.J. Wonnacott. 1990. Inleidende statistieken. 5e druk. Wiley
- Wikipedia. Bemonsteringsfout. Hersteld van: en.wikipedia.com
- Wikipedia. Foutmarge. Hersteld van: en.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.