
Schuifspanning hoe het wordt berekend en oefeningen worden opgelost
Het is bekend als afschuifsterkte Het resultaat van het uitoefenen van twee krachten parallel aan een oppervlak en in tegengestelde richting. Op deze manier kan een object in twee delen worden verdeeld, waardoor de secties over elkaar heen schuiven..
Directe afschuifkrachten worden dagelijks uitgeoefend op stoffen, papier of metalen, uitgeoefend door scharen, guillotines of scharen. Ze komen ook voor in constructies zoals bouten of schroeven, pluggen, balken, wiggen en lassen..

Het is noodzakelijk om duidelijk te maken dat het niet altijd bedoeld is om te snijden of te snijden, maar de schuifspanning heeft de neiging om het object waarop het wordt aangebracht te vervormen; daarom hebben balken die aan schuifspanning worden blootgesteld de neiging om onder hun eigen gewicht door te zakken. De volgende voorbeelden verduidelijken het punt.
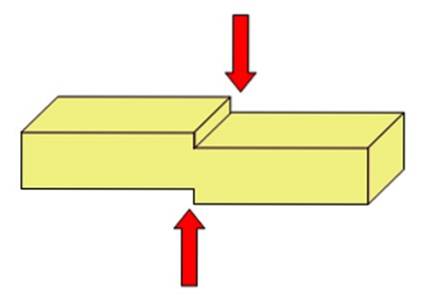
Figuur 2 toont een eenvoudig diagram om het bovenstaande te illustreren. Het is een object waarop twee krachten in tegengestelde richtingen werken. Er is een denkbeeldig snijvlak (het is niet getekend) en de krachten werken één aan elke kant van het vlak, waardoor de staaf in tweeën wordt gesneden.
In het geval van een schaar: elk blad of elke snede oefent een kracht uit op de doorsnede (cirkelvormig) van het te snijden object en verdeelt het ook in twee delen, zoals het touwtje in figuur 1.
Artikel index
- 1 Afschuifspanning kan vervorming veroorzaken
- 2 Hoe wordt de schuifspanning berekend??
- 3 Afschuifspanning en vervorming
- 4 Opgeloste oefeningen
- 4.1 -Oefening 1
- 4.2 -Oefening 2
- 5 referenties
Afschuifspanning kan vervorming veroorzaken
U kunt proberen een snijkracht uit te oefenen door uw hand over de kaft van een gesloten boek te schuiven. Het andere deksel moet op de tafel blijven zitten, wat kan worden bereikt door de vrije hand te ondersteunen zodat deze niet beweegt. Het boek vervormt een beetje met deze actie, zoals beschreven in de volgende afbeelding:
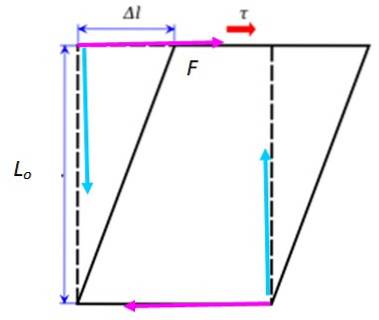
Als deze situatie zorgvuldig wordt geanalyseerd, worden de twee krachten al genoemd, maar deze keer toegepast horizontaalin fuchsia. De ene is die van je hand aan de ene kant en de andere wordt aangebracht door het oppervlak van de tafel aan de andere kant van het boek dat is bevestigd.
Het boek draait niet, hoewel deze krachten een netto koppel of moment kunnen veroorzaken. Om dit te voorkomen zijn er de andere twee verticale krachten (in turkoois); de ene toegepast met de andere hand en de normale uitgeoefend door de tafel, waarvan het netto moment in de tegenovergestelde richting werkt, waardoor de roterende beweging wordt voorkomen.
Hoe wordt de schuifspanning berekend?
Schuifspanningen treden zelfs in het menselijk lichaam op, aangezien het circulerende bloed continu tangentiële krachten uitoefent aan de binnenkant van de bloedvaten, waardoor kleine vervormingen in de wanden ontstaan..
Uw overweging is belangrijk bij het bepalen van de kans dat een structuur mislukt. Bij de afschuifkrachten wordt niet alleen rekening gehouden met de kracht, maar ook met het gebied waarop deze inwerkt.
Dit wordt onmiddellijk begrepen door twee cilindrische staven van dezelfde lengte, gemaakt van hetzelfde materiaal maar van verschillende dikte, te nemen en deze aan toenemende spanningen te onderwerpen totdat ze breken..
Het is duidelijk dat de noodzakelijke krachten heel anders zullen zijn, omdat de ene staaf dunner is dan de andere; de inspanning zal echter hetzelfde zijn.
Afschuifspanning wordt aangegeven met de Griekse letter τ (tau) en wordt berekend als het quotiënt tussen de grootte van de uitgeoefende kracht F. en het gebied NAAR van het oppervlak waarop het inwerkt:
τgemiddelde= F / A
De aldus berekende inspanning is degene die een gemiddelde kracht op het betreffende oppervlak produceert, aangezien de kracht niet op een enkel punt op het oppervlak inwerkt, maar over het geheel wordt verdeeld en niet uniform. De verdeling kan echter worden weergegeven door een resulterende kracht die op een bepaald punt inwerkt.
Afschuifspanningsafmetingen zijn kracht op het oppervlak. In eenheden van het internationale systeem komen ze overeen met newton / vierkante meter, een eenheid genaamd Pascal en afgekort Pa.
Het zijn dezelfde eenheden van druk, dus de eenheden van het Engelse systeem als pond-kracht / voet twee en pondkracht / inchtwee zijn ook geschikt.
Afschuifspanning en vervorming
In veel situaties is de grootte van de schuifspanning evenredig met de spanning die in het object wordt veroorzaakt, zoals in het vorige voorbeeldboek, dat terugkeert naar zijn oorspronkelijke afmetingen zodra de hand wordt verwijderd. In dat geval:
Afschuifsterkte ∝ Vervorming van het apparaat
De evenredigheidsconstante is in dit geval de afschuifmodulus, stijfheidsmodulus of afschuifmodulus (G):
Afschuifspanning = afschuifmodulus x rek per eenheid
τ = G. γ
Met γ = ΔL / Lof, waar ΔL. is het verschil tussen de uiteindelijke en initiële lengte. Door de gegeven vergelijkingen te combineren, kan een uitdrukking voor de rek veroorzaakt door spanning worden gevonden:
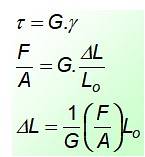
De waarde van de constante G Het wordt gevonden in tabellen en de eenheden zijn dezelfde als die voor spanning, aangezien de rek dimensieloos is. Bijna altijd de waarde van G is de helft of een derde van de waarde van EN, elasticiteitsmodulus.
In feite zijn ze gerelateerd door de uitdrukking:
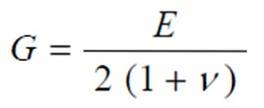
Waar ν de Poisson-modulus is, een andere elastische constante van het materiaal waarvan de waarde tussen 0 en ½ ligt. Juist daarom ligt G op zijn beurt tussen E / 3 en E / 2.
Opgeloste oefeningen
-Oefening 1
Om twee ijzeren platen te verbinden wordt een stalen schroef gebruikt, die afschuifkrachten tot 3200 N moet kunnen weerstaan. Wat is de minimale diameter van de schroef als de veiligheidsfactor 6,0 is? Het is bekend dat het materiaal tot 170 x 10 kan bevatten6 N / mtwee.
Oplossing
De schuifspanning waaraan de schroef wordt blootgesteld, wordt veroorzaakt door de krachten die in de onderstaande afbeelding worden weergegeven. De veiligheidsfactor is een dimensieloze grootheid en houdt verband met de maximaal toelaatbare spanning:
Afschuifspanning = F / A = Maximaal toelaatbare spanning / veiligheidsfactor
Daarom is het gebied:
A = F x veiligheidsfactor / schuifspanning = 3200 x 6/170 x 106 = 0.000113 mtwee
De oppervlakte van de schroef wordt gegeven door πDtwee/ 4, daarom is de diameter:
Dtwee= 4 x EEN / π = 0,000144 mtwee
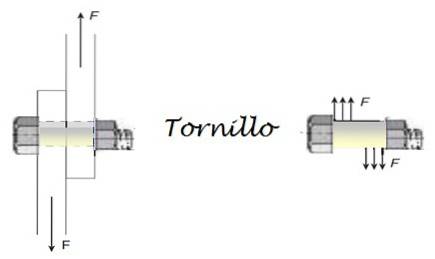
D = 0,012 m = 12 mm.
-Oefening 2
Een houten plug of plug wordt gebruikt om te voorkomen dat de katrol onder spanning draait T1 Y Ttwee, ten opzichte van een 3-inch as. De afmetingen van de pen zijn weergegeven in de afbeelding. Bepaal de grootte van de schuifspanning op het blok, als de weergegeven krachten op de poelie werken:
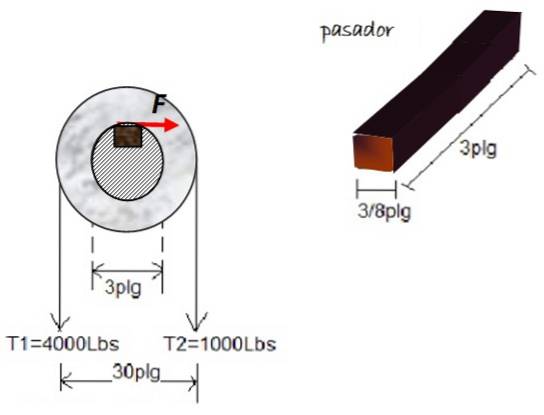
Oplossing
T1 produceert een koppel tegen de klok in op de poelie, waaraan een positief teken is toegewezen, terwijl Ttwee produceert koppel met de klok mee met een negatief teken. De hefboomarm meet 15 inch voor elke spanning. Daarom:
Netto koppel = 4000 pondkracht. 15 inch - 1000 pondkracht. 15 inch = 45.000 pondkracht. inch
Het houten blok mag niet roteren, daarom moeten de momenten ten opzichte van het midden van het blok nul zijn. F. vertegenwoordigt de gemiddelde kracht op het oppervlak:
45.000 - F.d = 0
Met d = 1,5 inch, Dus:
F x 1,5 = 45.000
F = 30.000 pondkracht
Deze kracht veroorzaakt een schuifspanning van grootte:
τ = F / A = 30.000 pondkracht / (3/8 x 3) inchtwee = 2,67 x 104 pondkracht / inchtwee
Referenties
- Beer, F. 2010. Mechanica van materialen. 5e. Editie. McGraw Hill. 7 - 9.
- Fitzgerald, 1996. Mechanics of Materials. Alpha Omega. 21-23.
- Giancoli, D. 2006. Natuurkunde: principes met toepassingen. 6th Ed Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Mechanica van materialen. 6e. Editie. Pearson Education. 22-25
- Valera Negrete, J. 2005. Opmerkingen over algemene fysica. UNAM. 87-98.
- Wikipedia. Schuifspanning. Hersteld van: en.wikipedia.org.



Niemand heeft nog op dit artikel gereageerd.