
Beschrijvende en inferentiële statistieken

De Beschrijvende statistieken Het is de verzameling statistische methoden die een groep gegevens beschrijven en / of karakteriseren. De inferentiële statistieken tracht af te leiden en conclusies te trekken over algemene situaties die verder gaan dan de verzamelde gegevens.
Statistiek is een discipline die verantwoordelijk is voor het verwerken en organiseren van gegevens, waarbij de gegevens elke maat of waarde zijn die kan worden verkregen door middel van experimenten, enquêtes, tellingen of andere middelen. Gegevensanalyse begint meestal met de toepassing van beschrijvende statistische methoden, en gaat dan verder met inferentiële statistische methoden..
| Beschrijvende statistieken | Inferentiële statistieken | |
|---|---|---|
| Definitie | Methoden die worden gebruikt om de belangrijkste kenmerken van bekende gegevens samen te vatten. | Methoden waarbij steekproefgegevens worden gebruikt om generalisaties of gevolgtrekkingen over een populatie te maken. |
| doelen | Karakteriseer een gegevensgroep Onderzoek trends of distributies | Onderzoek verschillen tussen groepen. Onderzoek of variabelen zijn gekoppeld. Vergelijk gemiddelden tussen groepen. Voorspel de ene variabele van de andere. |
| Analysemethoden | Maatregelen van centrale tendens:
Maatregelen van variabiliteit:
|
|
| Toepassingsgebieden | Natuurlijke en sociale wetenschappen | Sociale en natuurwetenschappen |
| Voorbeelden |
|
|
Wat zijn beschrijvende statistieken?
De Beschrijvende statistieken Het is het deel van de statistieken dat de gegevens rangschikt, zodat ze kunnen worden geanalyseerd en geïnterpreteerd. Beschrijvende statistische methoden stellen ons in staat om:
- Bepalen centrale tendens van een variabele: gemiddelde of rekenkundig gemiddelde, mediaan of modus.
- Bepalen variabiliteit van een variabele: standaarddeviatie, variantie, bereiken.
- Bepaal wat de verdeling van een variabele: frequentiehistogram, normale verdeling.
Beschrijvende statistische voorbeelden
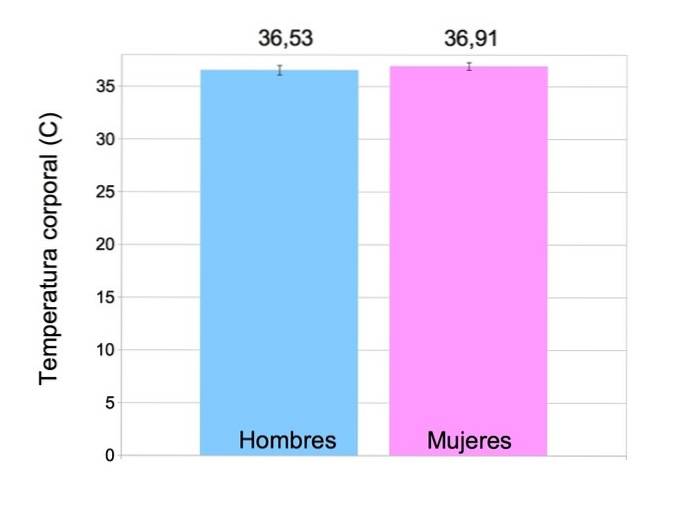
Als je een groep individuen wilt karakteriseren, gebruik je beschrijvende statistieken. We hebben bijvoorbeeld de volgende lichaamstemperatuurgegevens voor een groep mannen en vrouwen:
| Mannen | Dames |
|---|---|
| 36.1 | 36,2 |
| 35,9 | 37,2 |
| 36,0 | 37.3 |
| 36,4 | 37,1 |
| 36.3 | 37,0 |
| 36,7 | 37,2 |
| 36,9 | 36,9 |
| 36,8 | 36,8 |
| 37,2 | 36,4 |
| 37,0 | 37,0 |
Zoals ze worden gepresenteerd, kunnen we geen conclusie trekken, maar wanneer we beschrijvende statistische technieken toepassen, kunnen we zeggen dat:
- mannen in deze groep hebben een gemiddelde temperatuur van 36,53 ° C met een standaarddeviatie van 0,45;
- vrouwen in deze groep hebben een gemiddelde temperatuur van 36,91 ºC, met een standaarddeviatie van 0,36.
Wat zijn inferentiële statistieken?
De inferentiële statistieken of statistische gevolgtrekking is het deel van de statistieken dat tot doel heeft kenmerken of verwachte resultaten van een populatie te voorspellen of af te leiden, op basis van de gegevens die zijn verkregen uit een steekproef van die populatie. Onder de technieken die worden toegepast in inferentiële statistieken zijn er:
- De t-test: wordt gebruikt om het rekenkundig gemiddelde van twee groepen te vergelijken door te bepalen of de verschillen tussen de groepen willekeurig voorkomen of systematisch een reëel verschil aangeven.
- Variantieanalyse of ANOVA: toegepast om twee of meer groepen variabelen te vergelijken.
- De correlatieanalyse: laat zien of de waarden tussen twee variabelen de neiging hebben om systematisch te veranderen. Om deze bepalingen uit te voeren, wordt de correlatiecoëfficiënt gebruikt r en de waarde van p of betrouwbaarheidsinterval CI.
- Regressie analyse: voorspelt de ene waarde van de andere.
Voorbeelden van inferentiële statistieken
Als we willen bepalen of enig gedrag of biologische toestand verband houdt met een ziekte, gebruiken we inferentiële statistische methoden. In een onderzoek dat in Duitsland werd uitgevoerd, werden bijvoorbeeld 3109 mensen bijna zeven jaar lang geëvalueerd op verschillende gezondheidsparameters. De resultaten toonden aan dat hoge bloedglucosespiegels (meer dan 126 mg / dl vasten), roken en lichamelijke inactiviteit geassocieerd waren met de ontwikkeling van dementie..
Wanneer een nieuw medicijn wordt ontdekt en de effectiviteit ervan moet worden aangetoond bij een bepaalde ziekte, worden inferentiële statistieken gebruikt. In dit geval worden de effecten van een groep behandeld met het medicijn en een andere groep behandeld met een placebo of een controlemedicijn vergeleken..
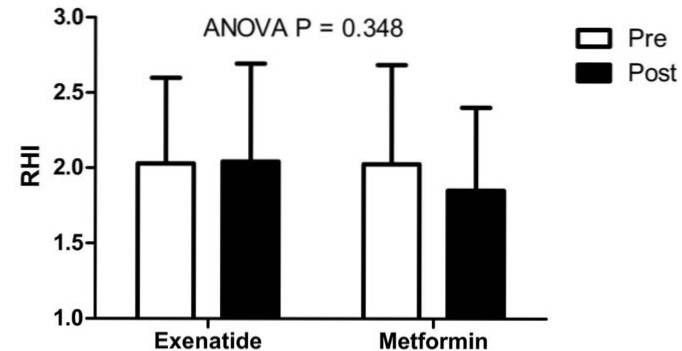
De groep van Kelly et al. Onderzocht de endotheelfunctie bij 50 zwaarlijvige personen vóór (Pre) en na (Post) drie maanden behandeling met twee geneesmiddelen: exenatide en metformine (controle). Bij het analyseren van de resultaten met de ANOVA-techniek (P = 0,348; inferentiële statistieken) ontdekten ze dat exenatide geen effect had op de endotheelfunctie, vergeleken met metformine..
Referenties
Hessler, J.B., Ander, K-H, Brönner, M. et al. (2016) Voorspellen van dementie bij eerstelijns patiënten met een cardiovasculaire gezondheidsmaatstaf: een prospectieve populatie-gebaseerde studie. BMC Neurol. 16: 116.
Kelly, A.S., Bergenstal, R.M., Gonzalez-Campoy, J.M., Katz, H., Bank, A.J. (2012) Effecten van Exenatide versus Metformine op de endotheelfunctie bij obese patiënten met prediabetes: een gerandomiseerde studie. Cardiovasculaire diabetes 11:64.



Niemand heeft nog op dit artikel gereageerd.