Flux van elektrisch veld

Wat is een elektrische veldflux?

De elektrische veldstroom of simpelweg elektrische flux is een scalaire hoeveelheid die evenredig is met het aantal elektrische veldlijnen dat door een oppervlak gaat. Het wordt aangeduid met de Griekse hoofdletter Φ (phi).

Het elektrische veld "stroomt" eigenlijk niet zoals een stroom water dat doet, hoewel de stroomlijnen van de vloeistof lijken op die van het elektrische veld..

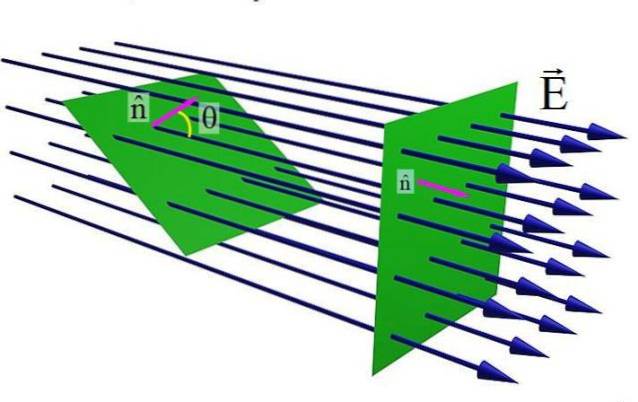
De bovenstaande afbeelding toont een plat oppervlak dat wordt doorkruist door een elektrisch veld EN. Wanneer de eenheidsvector loodrecht op het oppervlak staat n en het veld EN parallel zijn, is het aantal veldlijnen dat het oppervlak kruist maximaal. Maar als de hoek θ tussen n Y EN, het aantal lijnen dat door het groene oppervlak gaat, is minder.

Aan de andere kant hangt de flux van het elektrische veld ook af van de grootte van EN, want hoe groter deze, hoe meer veldlijnen het oppervlak kruisen. En natuurlijk, hoe groter het gebied S van dat oppervlak, hoe groter de stroom, dus de volgende vergelijking wordt vastgesteld:

Φ = E ∙ Scosθ

Deze uitdrukking komt overeen met het puntproduct tussen de vectoren EN Y n​

Φ = (EN ​ n) S

De eenheid voor elektrische veldflux in het SI International System of Units is N.m^twee/ C (Newton x vierkante meter / coulomb). Als alternatief, aangezien het veld ook wordt gemeten in V / m (volt over meter), blijft de elektrische flux in (V ∙ m).

Voorbeelden

Volgens de definitie kan de elektrische flux positief, negatief of gelijk zijn aan 0. De elektrische veldflux is:

-Positief wanneer hoek θ tussen EN Y n is kleiner dan 90º, aangezien cos θ groter is dan nul.

-Negatief als die hoek groter is dan 90º, want dan is cos θ kleiner dan nul.

-Null als θ exact 90º is, omdat cos 90º = 0 en de veldlijnen in dit geval tangentieel aan het oppervlak zijn.

-Aan de andere kant, als de hoek tussen EN Y n gelijk is aan 0, krijgt de stroom zijn maximale waarde.

Deze mogelijkheden worden getoond in de volgende afbeelding:

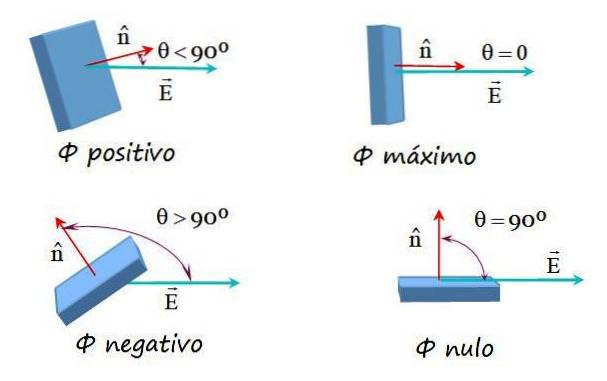
Elektrische veldflux op een willekeurig oppervlak

Eerder werd de flux van het elektrische veld bepaald in het specifieke geval van een uniform veld dat op een vlak oppervlak invalt. Voor een oppervlak met een willekeurige vorm S en / of een niet-uniform elektrisch veld is de hoek tussen EN Y n kan van punt tot punt verschillen.

In de volgende afbeelding zijn er twee voorbeelden, links een gebogen vlak en rechts een gesloten vlak.

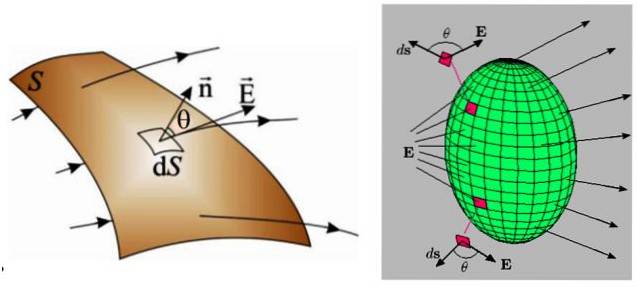
In beide gevallen is het oppervlak verdeeld in veel kleinere gebieden, van oneindig kleine afmetingen, dS genaamd, waar een stroom ook oneindig dΦ doorheen gaat:

dΦ = (EN​n) dS = (Ecosθ) dS

Het totale veld wordt verkregen door al deze oneindig kleine bijdragen toe te voegen:

Bij gesloten oppervlakken, n wijst altijd naar buiten, daarom heeft de stroom een ​​+ -teken wanneer deze saillant is voor S, aangezien de hoek ertussen EN Y n is minder dan 90º, en teken - wanneer het veld binnenkomt, want dan is de hoek ertussen EN Y n is groter dan 90º (zie figuur 2).

Merk op dat in het gesloten oppervlak aan de rechterkant het aantal veldlijnen dat het oppervlak binnenkomt gelijk is aan het aantal lijnen dat het oppervlak verlaat. Daarom is de netto stroom, gedefinieerd als de algebraïsche som van de inkomende stroom en de uitgaande stroom, nul.

De bron van het elektrische veld bevindt zich in dit geval buiten het oppervlak, maar de netto flux zou anders zijn dan 0 als de bron van het elektrische veld (de verdeling van ladingen) zich binnen het oppervlak bevond..

Opleiding

Oefening 1

Het heeft een elektrisch veld EN = 3,5 kN / C X en een vlak rechthoekig oppervlak van 0,35 m breed en 0,7 m lang. Zoek de elektrische veldflux door de rechthoek in de volgende gevallen:

a) Het oppervlak is evenwijdig aan het yz-vlak.

b) De rechthoek is evenwijdig aan het xy-vlak.

c) De normaal van het vlak vormt een hoek van 40º met de x-as en bevat de y-as.

Oplossing voor

De normaalvector en de elektrische veldvector zijn parallel, daarom is de hoek θ ertussen 0º en is de elektrische flux:

Φ = (E ∙ S) cos 0 = E ∙ S

Het gebied S van de rechthoek is:

S = 0,35 mx 0,7 m = 0,245 m^twee

Vervangen in Φ:

Φ = E ∙ S = 3,5 x 10³ N / C × 0,245 m^twee = 857,5 N ∙ m^twee / C.

Oplossing b

De flux van het elektrische veld is 0, aangezien de vectoren EN Y n loodrecht op elkaar staan.

Oplossing c

De hoek θ tussen het veld EN en de normale vector n is 40º (zie figuur), dus:

Φ = E ∙ S ∙ cos θ = 3,5 x 10³ N / C × 0,245 m^twee × cos 40º = 656,9 N ∙ m^twee / C.

Oefening 2

Bereken de flux van het elektrische veld die een positieve puntlading q produceert_of = 2 μC gelegen in het midden van een bol met straal R = 5 cm.

Oplossing

Het veld geproduceerd door de lading q_of Het is niet uniform, maar uit de wet van Coulomb is bekend dat het op het oppervlak van de bol een grootte heeft van:

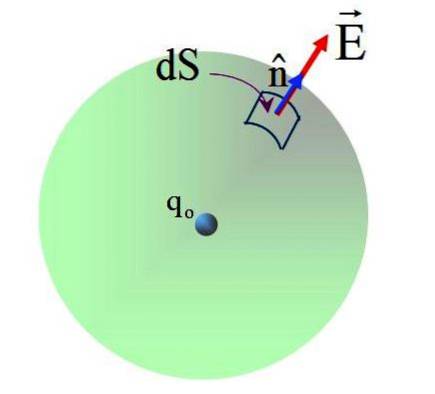
Het veld heeft een radiale richting en de normaalvector n, daarom is de hoek tussen beide vectoren 0 op elk punt op het bolvormige oppervlak. Vervangen in:

Het moet:

De integraal van dS over het gehele bolvormige oppervlak S is het gebied, dat 4πR is^twee, Dus:

De waarde is:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m^twee/ C = 2,3 x 10⁵ N⋅m^twee/ C

Referenties

1. Bauer, W. 2011. Physics for Engineering and Sciences. Deel 1. Mc Graw Hill.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 5. Elektrostatica. Bewerkt door Douglas Figueroa (USB).
3. Giambattista, A. 2010. Physics. 2e. Ed McGraw Hill.
4. Giancoli, D. 2006. Natuurkunde: principes met toepassingen. 6e. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. Ed. Deel 1. Pearson.