De volumestroom het laat toe het vloeistofvolume te bepalen dat door een gedeelte van de leiding gaat, en geeft een maat voor de snelheid waarmee het fluïdum erdoorheen beweegt. Daarom is de meting vooral interessant op uiteenlopende gebieden, zoals onder meer de industrie, de geneeskunde, de bouw en het onderzoek..
Het meten van de snelheid van een vloeistof (of het nu een vloeistof, een gas of een mengsel van beide is) is niet zo eenvoudig als het meten van de verplaatsingssnelheid van een vast lichaam. Daarom komt het voor dat om de snelheid van een vloeistof te kennen, het nodig is om de stroom ervan te kennen.
Deze en vele andere vragen met betrekking tot vloeistoffen worden behandeld door de tak van de fysica die bekend staat als vloeistofmechanica. Stroming wordt gedefinieerd als hoeveel vloeistof door een gedeelte van een leiding stroomt, of het nu een pijpleiding, een oliepijpleiding, een rivier, een kanaal, een bloedleiding, enz. Is, rekening houdend met een tijdelijke eenheid..
Het volume dat in een tijdseenheid door een bepaald gebied gaat, wordt meestal berekend, ook wel volumestroom genoemd. De massa of massastroom die op een bepaald moment door een bepaald gebied gaat, wordt ook gedefinieerd, hoewel deze minder vaak wordt gebruikt dan de volumestroom..
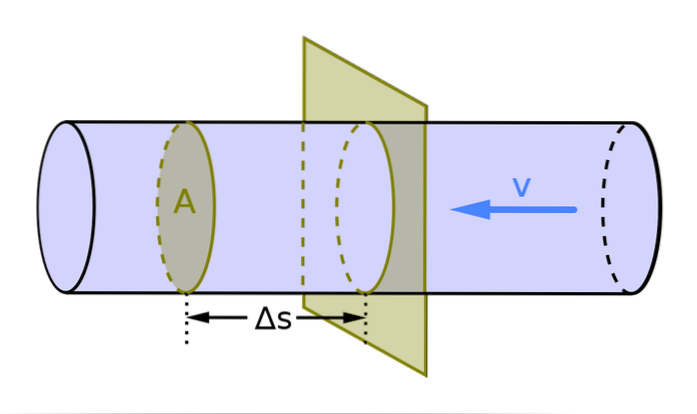
Het volumetrische debiet wordt weergegeven door de letter Q. Voor de gevallen waarin het debiet loodrecht op het geleidergedeelte beweegt, wordt dit bepaald met de volgende formule:
Q = A = V / t
In deze formule is A het gedeelte van de geleider (het is de gemiddelde snelheid van de vloeistof), V is het volume en t is de tijd. Omdat in het internationale systeem het gebied of de sectie van de geleider wordt gemeten in mtwee en de snelheid in m / s, de stroming wordt gemeten m3/ s.
Voor de gevallen waarin de snelheid van de vloeistofverplaatsing een hoek θ creëert met de richting loodrecht op het oppervlaktegedeelte A, is de uitdrukking om de stroomsnelheid te bepalen de volgende:
Q = A cos θ
Dit is consistent met de vorige vergelijking, aangezien wanneer de stroming loodrecht op het gebied A staat, θ = 0 en dus cos θ = 1.
De bovenstaande vergelijkingen zijn alleen waar als de snelheid van de vloeistof gelijkmatig is en als het gebied van de sectie vlak is. Anders wordt de volumestroom berekend via de volgende integraal:
Q = ∫∫s v d S
In deze integraal is dS de oppervlaktevector, bepaald door de volgende uitdrukking:
dS = n dS
Daar is n de eenheidsvector loodrecht op het kanaaloppervlak en dS een oppervlaktedifferentiaalelement.
Een kenmerk van onsamendrukbare vloeistoffen is dat de massa van de vloeistof wordt behouden door middel van twee secties. Om deze reden is aan de continuïteitsvergelijking voldaan, die de volgende relatie tot stand brengt:
ρ1 NAAR1 V.1 = ρtwee NAARtwee V.twee
In deze vergelijking is ρ de dichtheid van de vloeistof.
Voor de gevallen van regimes in permanente stroom, waarin de dichtheid constant is en daarom is het waar dat ρ1 = ρtwee, komt neer op de volgende uitdrukking:
NAAR1 V.1 = Atwee V.twee
Dit komt overeen met bevestigen dat de stroom behouden blijft en daarom:
Q1 = Qtwee.
Uit de observatie van het bovenstaande volgt dat vloeistoffen versnellen wanneer ze een smaller gedeelte van een leiding bereiken, terwijl ze vertragen wanneer ze een groter gedeelte van een leiding bereiken. Dit feit heeft interessante praktische toepassingen, omdat het spelen met de bewegingssnelheid van een vloeistof mogelijk maakt.
Het principe van Bernoulli bepaalt dat voor een ideale vloeistof (dat wil zeggen een vloeistof die noch viscositeit noch wrijving heeft) die in circulatie door een gesloten leiding beweegt, zijn energie constant blijft gedurende zijn gehele verplaatsing..
Uiteindelijk is het principe van Bernoulli niets meer dan de formulering van de wet van behoud van energie voor de stroming van een vloeistof. De vergelijking van Bernoulli kan dus als volgt worden geformuleerd:
h + vtwee / 2g + P / ρg = constant
In deze vergelijking is h de hoogte en is g de versnelling als gevolg van de zwaartekracht.
De Bernoulli-vergelijking houdt rekening met de energie van een vloeistof op elk moment, een energie die uit drie componenten bestaat.
In dit geval wordt de vergelijking van Bernoulli als volgt uitgedrukt:
h ρ g + (vtwee ρ) / 2 + P = constant
Logischerwijs wordt in het geval van een echte vloeistof de uitdrukking van de Bernoulli-vergelijking niet vervuld, aangezien wrijvingsverliezen optreden bij de vloeistofverplaatsing en het noodzakelijk is om toevlucht te nemen tot een complexere vergelijking.
De volumestroom wordt beïnvloed als er een obstructie in het kanaal is.
Bovendien kan het volumetrische debiet ook veranderen als gevolg van variaties in temperatuur en druk in de echte vloeistof die door een leiding beweegt, vooral als dit een gas is, aangezien het volume dat een gas inneemt varieert als een functie van de temperatuur en druk. Bij.
Een heel eenvoudige methode om de volumestroom te meten, is om een vloeistof gedurende een bepaalde tijd in een doseertank te laten stromen..
Deze methode is over het algemeen niet erg praktisch, maar de waarheid is dat het buitengewoon eenvoudig en zeer illustratief is om de betekenis en het belang van het kennen van de stroomsnelheid van een vloeistof te begrijpen..
Op deze manier kan de vloeistof een tijdlang in een meettank stromen, wordt het verzamelde volume gemeten en wordt het verkregen resultaat gedeeld door de verstreken tijd.
Niemand heeft nog op dit artikel gereageerd.