De statische wrijving is de kracht die ontstaat tussen twee oppervlakken wanneer het ene oppervlak niet schuift ten opzichte van het andere. Het is van groot belang, omdat het ons in staat stelt om vooruit te gaan tijdens het lopen, omdat het de kracht is die aanwezig is tussen de vloer en de zool van de schoenen..
Het is ook de statische wrijving die optreedt tussen de stoep en de banden van de auto. Als deze kracht niet aanwezig is, kan de auto niet in beweging komen, zoals gebeurt bij een auto die probeert te starten op een ijzige ondergrond: de wielen glijden maar de auto beweegt niet.
Statische wrijving hangt af van de ruwheid van de oppervlakken die in contact komen en ook van het soort materiaal waaruit ze zijn gemaakt. Daarom zijn de banden en sportschoenen gemaakt van rubber, om de wrijving met de stoep te vergroten..
In het statische wrijvingsmodel worden de eigenschappen van de materialen en de mate van ruwheid tussen de oppervlakken samengevat in een nummer genaamd statische wrijvingscoëfficiënt, die experimenteel wordt bepaald.
Artikel index
Bovenstaande figuur toont een boek dat in rust ligt op een tafel met een hellingshoek van 15,7º.
Als de oppervlakken van het boek en de tafel erg glad en gepolijst waren, kon het boek niet stilstaan. Maar omdat ze dat niet zijn, verschijnt er een kracht die raakt aan de contactoppervlakken, de kracht van statische wrijving.
Als de hellingshoek groot genoeg is, is er niet genoeg statische wrijvingskracht om het boek in evenwicht te brengen en het zou gaan glijden.
In dit geval is er ook wrijving tussen het boek en de tafel, maar dat zou een de sterkte van dynamische wrijving, ook wel genoemd kinetische wrijving.
Er is een grens tussen statische wrijving en dynamische wrijving, die optreedt tegen de tijd dat de statische wrijving zijn maximale waarde bereikt.
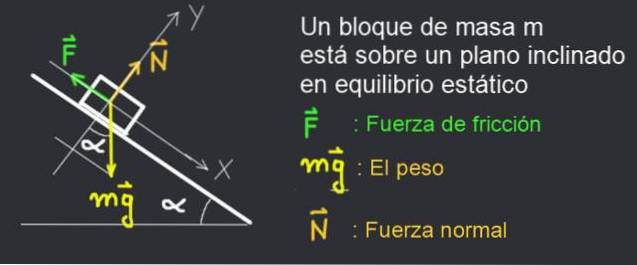
Laten we in figuur 2 eens kijken naar het krachtdiagram van een boek met massa m dat in rust wordt gehouden op een hellingsvlak α.
Het boek blijft liggen omdat de statische wrijvingskracht F het systeem in evenwicht houdt.
Als de hellingshoek iets toeneemt, moeten de contactvlakken meer wrijvingskracht leveren, maar de hoeveelheid statische wrijving die de contactvlakken kunnen leveren heeft een maximale limiet Fmax. hoogte, namelijk:
F ≤ Fmax. hoogte.
De maximale statische wrijvingskracht is afhankelijk van de materialen en de mate van ruwheid van de contactoppervlakken, evenals de stevigheid van de grip.
De statische wrijvingscoëfficiënt μen is een positief getal dat afhangt van de eigenschappen van de oppervlakken die in contact komen. Normale kracht N dat het vlak op het blok uitoefent, toont de mate van dichtheid tussen het oppervlak van het blok en het vlak. Dit is hoe ze de maximale wrijvingskracht bepalen die oppervlakken leveren als er niet glijdt:
F.max. hoogte = μen N
Samengevat volgt de statische wrijvingskracht het volgende model:
F ≤ μen N
De statische wrijvingscoëfficiënt is een dimensieloos getal dat experimenteel wordt bepaald voor elk paar oppervlakken.
In figuur 2 beschouwen we het blok in rust. De volgende krachten werken erop:
- Wrijvingskracht: F.
- Het gewicht van het massablok m: mg
- Normale kracht: N
Aangezien het blok in rust is en geen versnelling heeft, is volgens de tweede wet van Newton de resulterende kracht -een vectorsom- nul:
F. + N + mg 0
Een vast XY-coördinatensysteem wordt beschouwd met de X-as langs het hellende vlak en de Y-as er loodrecht op, zoals weergegeven in figuur 2.
De krachten moeten worden gescheiden volgens hun Cartesiaanse componenten, wat aanleiding geeft tot het volgende stelsel van vergelijkingen:
-Onderdeel X: -F + mg Sen (α) = 0
-Component Y: N - mg Cos (α) = 0
De waarde van de statische wrijvingskracht wordt opgelost uit de eerste vergelijking:
F = mg Sen (α)
En vanaf de tweede de waarde van de normaalkracht:
N = mg Cos (α)
De statische wrijvingskracht F volgt het volgende model:
F ≤ μen N
Vervanging van de eerder verkregen waarden in de ongelijkheid die we hebben:
mg Sen (α) ≤ μen mg Cos (α)
Rekening houdend met het feit dat voor waarden van α tussen 0º en 90º, de sinus- en cosinusfuncties beide positief zijn, en dat het quotiënt tussen de sinus en de cosinus de tangens is, hebben we:
Geelbruin (α) ≤ μen
De gelijkheid geldt voor een bepaalde waarde van α die we de kritische hoek noemen en die we aanduiden met α *, dat wil zeggen:
μen = Geelbruin (α *)
De kritische hoek wordt experimenteel bepaald, waarbij de helling geleidelijk toeneemt tot de juiste hoek waaronder het blok begint te glijden, dat is de kritische hoek α *.
In het boek van figuur 1 werd deze hoek experimenteel bepaald, resulterend in 24 °. Dan is de statische wrijvingscoëfficiënt:
μen = Geelbruin (24º) = 0,45.
Het is een positief getal tussen 0 en oneindig. Als μen = 0 de oppervlakken zijn perfect glad. Als μen → ∞ de oppervlakken zijn perfect verbonden of gelast.
Over het algemeen ligt de waarde van de wrijvingscoëfficiënt tussen 0 en 10.
Bij sprint- of dragsterraces worden tijdens de start acceleraties tot wel 4g behaald, die precies worden bereikt wanneer de banden niet slippen ten opzichte van het wegdek..
Dit komt doordat de statische wrijvingscoëfficiënt altijd groter is dan de dynamische wrijvingscoëfficiënt..
Ervan uitgaande dat het totale gewicht van het voertuig plus de bestuurder 600 kg is en dat de achterwielen 80% van het gewicht dragen, bepaal dan de kracht van statische wrijving tijdens de start van 4 g en de coëfficiënt van statische wrijving tussen de banden en het wegdek..
Volgens de tweede wet van Newton is de resulterende kracht gelijk aan de totale massa van het voertuig maal de versnelling die het verkrijgt.
Aangezien het voertuig in verticaal evenwicht is, vallen het normale gewicht en het gewicht weg, waardoor de wrijvingskracht F die de stoep uitoefent op het contactoppervlak van de tractiewielen als gevolg daarvan overblijft, waardoor:
F = m (4 g) = 600 kg (4 x 9,8 m / stwee) = 23520 N = 2400 kg-f
Dit betekent dat de trekkracht 2,4 ton is.
De wrijvingskracht die het wiel op de grond uitoefent, gaat achteruit, maar de reactie, die hetzelfde en tegengesteld is, werkt op de band en gaat vooruit. Dat is de kracht die het voertuig aandrijft.
Al deze kracht wordt natuurlijk geproduceerd door de motor die de vloer door het wiel probeert terug te duwen, maar het wiel en de vloer zijn gekoppeld door wrijvingskracht..
Om de statische wrijvingscoëfficiënt te bepalen, gebruiken we het feit dat de verkregen F de maximaal mogelijke wrijving is, aangezien we de limiet van maximale versnelling hebben bereikt, daarom:
F = μen N = μe (0,8 mg)
Er is rekening gehouden met het feit dat de achterste aandrijfwielen 0,8 keer het gewicht dragen. Oplossend voor de wrijvingscoëfficiënt, verkrijgen we:
μen = F / (0,8 mg) = 23520 N / (0,8 x 600 kg x 9,8 m / s ^ 2) = 5.
Conclusie: μen = 5.
Niemand heeft nog op dit artikel gereageerd.