
Injectieve functie wat het is, waar het voor is en voorbeelden

EEN injectieve functie is elke relatie van elementen van het domein met een enkel element van het codomein. Ook wel bekend als functie een voor een elf ), maken deel uit van de classificatie van functies met betrekking tot de manier waarop hun elementen met elkaar in verband staan.
Een element van het codomain kan alleen de afbeelding zijn van een enkel element van het domein, op deze manier kunnen de waarden van de afhankelijke variabele niet worden herhaald.
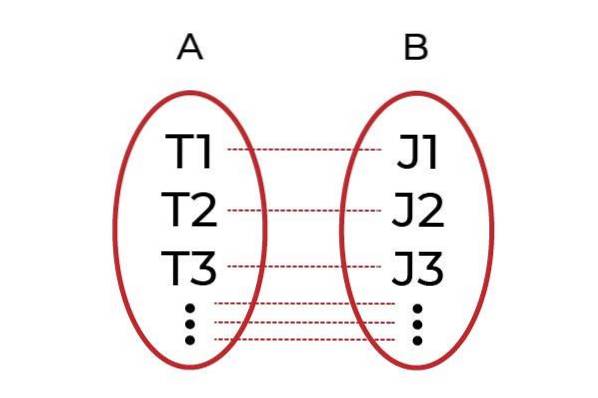
Een duidelijk voorbeeld is het groeperen van mannen met banen in groep A en in groep B alle bazen. De functie F. Het zal degene zijn die elke werknemer met zijn baas associeert. Als elke werknemer wordt geassocieerd met een andere baas door F., dan F. zal een ... zijn injectieve functie.
Overwegen injectief voor een functie moet het volgende worden vervuld:
∀ x1 ≠ xtwee ⇒ F (x1 ) ≠ F (xtwee
Dit is de algebraïsche manier om te zeggen Voor alle x1 verschillend van xtwee je hebt een F (x1 ) verschillend van F (xtwee .
Artikel index
- 1 Waar zijn de injectiefuncties voor?
- 1.1 Functieconditionering
- 2 Voorbeelden van injectiefuncties met opgeloste oefeningen
- 2.1 Voorbeeld 1
- 2.2 Voorbeeld 2
- 2.3 Voorbeeld 3
- 2.4 Voorbeeld 4
- 2.5 Voorbeeld 5
- 2.6 Voorbeeld 6
- 2.7 Voorbeeld 7
- 3 Oefeningen voorgesteld voor klas / thuis
- 4 referenties
Waar zijn injectieve functies voor?
Injectiviteit is een eigenschap van continue functies, aangezien ze zorgen voor de toewijzing van afbeeldingen voor elk element van het domein, een essentieel aspect in de continuïteit van een functie..
Bij het tekenen van een lijn parallel aan de as X op de grafiek van een injectieve functie, mag u de grafiek slechts op één punt aanraken, ongeacht de hoogte of grootte van Y de lijn is getrokken. Dit is de grafische manier om de injectiviteit van een functie te testen.
Een andere manier om te testen of een functie is injectief, lost op voor de onafhankelijke variabele X in termen van de afhankelijke variabele Y. Vervolgens moet worden geverifieerd of het domein van deze nieuwe uitdrukking de reële getallen bevat, op hetzelfde moment als voor elke waarde van Y er is een enkele waarde van X.
De functies of ordeningsrelaties gehoorzamen onder meer aan de notatie F: DF.CF.
Wat wordt gelezen F loopt van DF. tot CF.
Waar de functie F. relateren de sets Domein Y Codomain. Ook wel bekend als de startset en finishset.
De Dominion DF. bevat de toegestane waarden voor de onafhankelijke variabele. Het codomein CF. Het is samengesteld uit alle waarden die beschikbaar zijn voor de afhankelijke variabele. De elementen van CF. gerelateerd aan DF. staan bekend als Functiebereik (RF. .
Functieconditionering
Soms kan een functie die niet injectief is, aan bepaalde voorwaarden worden onderworpen. Deze nieuwe voorwaarden kunnen er een injectieve functie. Allerlei wijzigingen aan het domein en codomain van de functie zijn geldig, waarbij het doel is om de eigenschappen van injectiviteit in de bijbehorende relatie te vervullen.
Voorbeelden van injectiefuncties met opgeloste oefeningen
voorbeeld 1
Laat de functie F: R R gedefinieerd door de lijn F (x) = 2x - 3
A: [Alle reële getallen]
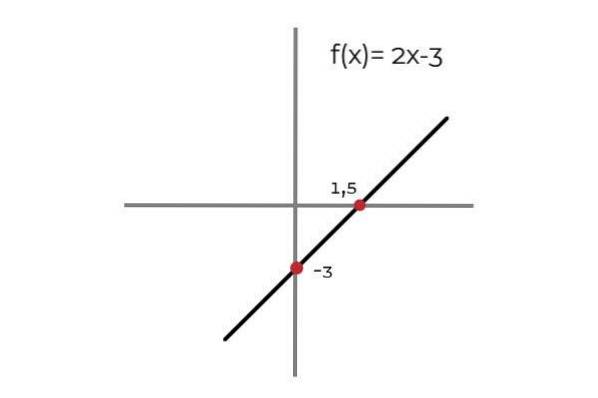
Opgemerkt wordt dat er voor elke waarde van het domein een afbeelding in het codomain staat. Deze afbeelding is uniek, wat F een injectieve functie maakt. Dit geldt voor alle lineaire functies (functies waarvan de grootste graad van de variabele één is).
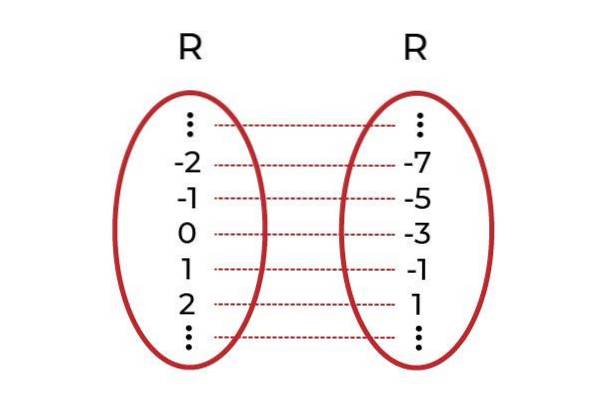
Voorbeeld 2
Laat de functie F: R R gedefinieerd door F (x) = xtwee +1
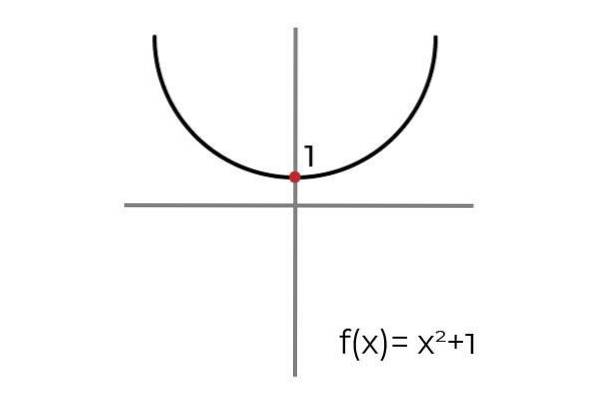
Bij het tekenen van een horizontale lijn wordt opgemerkt dat de grafiek meer dan eens wordt gevonden. Hierdoor is de functie F. het is niet injectief zolang het is gedefinieerd R R
We gaan verder met het conditioneren van het domein van de functie:
F: R+ OF 0 R
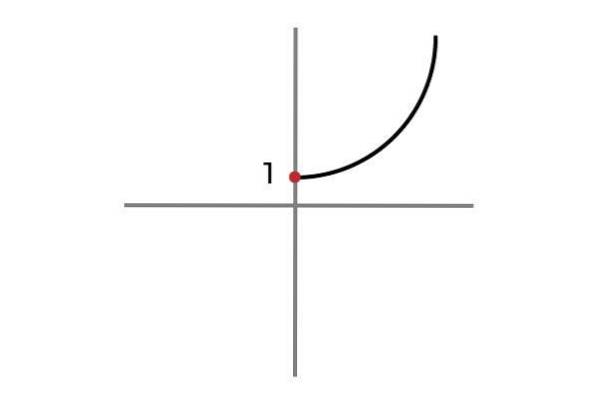
Nu neemt de onafhankelijke variabele geen negatieve waarden aan, op deze manier worden herhalende resultaten vermeden en wordt de functie F: R+ OF 0 R gedefinieerd door F (x) = xtwee + 1 is injectief.
Een andere homologe oplossing zou zijn om het domein naar links te beperken, dat wil zeggen om de functie te beperken tot alleen negatieve en nulwaarden.
We gaan verder met het conditioneren van het domein van de functie
F: R- OF 0 R
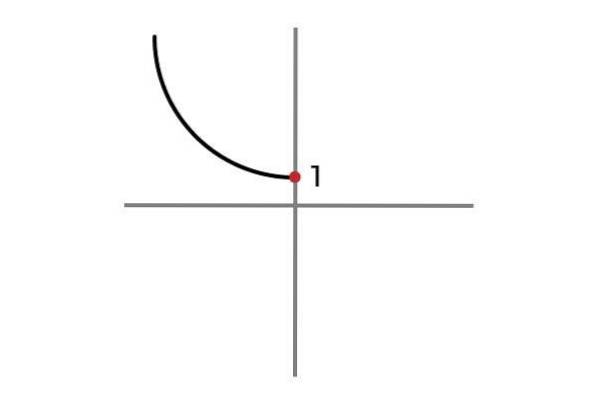
Nu neemt de onafhankelijke variabele geen negatieve waarden aan, op deze manier worden herhalende resultaten vermeden en wordt de functie F: R- OF 0 R gedefinieerd door F (x) = xtwee + 1 is injectief.
Goniometrische functies hebben gedrag dat lijkt op golven, waarbij het heel gebruikelijk is om herhalingen van waarden in de afhankelijke variabele te vinden. Door specifieke conditionering, gebaseerd op voorkennis van deze functies, kunnen we het domein verkleinen om aan de voorwaarden van injectiviteit te voldoen.
Voorbeeld 3
Laat de functie F: [ -π / 2, π / 2 ] → R. gedefinieerd door F (x) = Cos (x)
In de pauze -π / 2 → π / 2 de cosinusfunctie varieert de resultaten tussen nul en één.
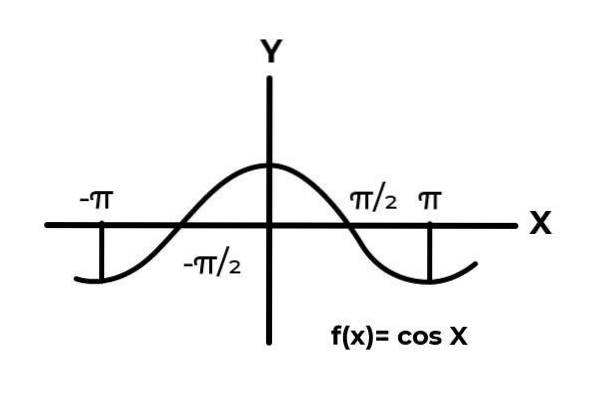
Zoals te zien is in de grafiek. Begin helemaal opnieuw x = -π / 2 bereikt dan een maximum bij nul. Het is na x = 0 dat de waarden beginnen te herhalen, totdat ze terugkeren naar nul in x = π / 2. Op deze manier is dat bekend F (x) = Cos (x) is niet injectief voor het interval -π / 2, π / 2 .
Bij het bestuderen van de grafiek van de functie F (x) = Cos (x) intervallen worden waargenomen waar het gedrag van de curve zich aanpast aan de injectiviteitscriteria. Zoals bijvoorbeeld het interval
[0 , π
Waar de functie varieert, resulteert van 1 tot -1, zonder een waarde in de afhankelijke variabele te herhalen.
Op deze manier functioneert de functie F: [0 , π ] → R. gedefinieerd door F (x) = Cos (x). Het is injectief
Er zijn niet-lineaire functies waarin vergelijkbare gevallen voorkomen. Voor uitdrukkingen van rationeel type, waarbij de noemer ten minste één variabele bevat, zijn er beperkingen die de injectiviteit van de relatie verhinderen.
Voorbeeld 4
Laat de functie F: R R gedefinieerd door F (x) = 10 / x
De functie is gedefinieerd voor alle reële getallen behalve 0 wie heeft een onbepaaldheid (kan niet worden gedeeld door nul).
Bij het naderen van nul van links neemt de afhankelijke variabele zeer grote negatieve waarden aan, en onmiddellijk na nul nemen de waarden van de afhankelijke variabele grote positieve waarden aan.
Deze verstoring veroorzaakt de uitdrukking F: R R gedefinieerd door F (x) = 10 / x
Wees niet injectief.
Zoals te zien is in de voorgaande voorbeelden, dient het uitsluiten van waarden in het domein om deze onbepaaldheden te "herstellen". We gaan verder met het uitsluiten van nul van het domein, waarbij de vertrek- en aankomstsets als volgt worden gedefinieerd:
R - 0 R
Waar R - 0 symboliseert de reals, behalve voor een set waarvan het enige element nul is.
Op deze manier de uitdrukking F: R - 0 R gedefinieerd door F (x) = 10 / x is injectief.
Voorbeeld 5
Laat de functie F: [0 , π ] → R. gedefinieerd door F (x) = Sen (x)
In de pauze [0 , π de sinusfunctie varieert de resultaten tussen nul en één.
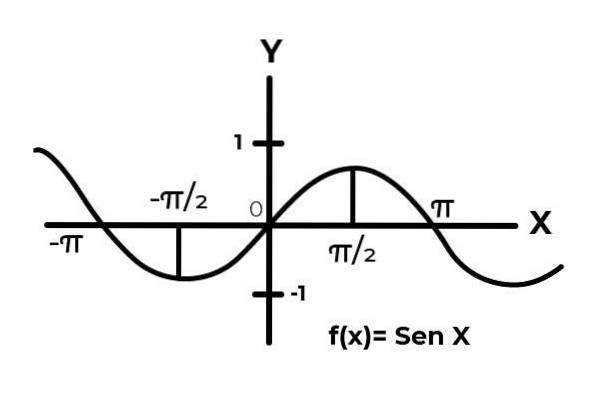
Zoals te zien is in de grafiek. Begin helemaal opnieuw x = 0 dan het bereiken van een maximum in x = π / 2. Het is na x = π / 2 dat de waarden beginnen te herhalen, totdat ze terugkeren naar nul x = π. Op deze manier is dat bekend F (x) = Sen (x) is niet injectief voor het interval [0 , π .
Bij het bestuderen van de grafiek van de functie F (x) = Sen (x) intervallen worden waargenomen waar het gedrag van de curve zich aanpast aan de injectiviteitscriteria. Zoals bijvoorbeeld het interval π / 2,3π / 2
Waar de functie varieert, resulteert van 1 tot -1, zonder een waarde in de afhankelijke variabele te herhalen.
Op deze manier de functie F: [ π / 2,3π / 2 ] → R. gedefinieerd door F (x) = Sen (x). Het is injectief
Voorbeeld 6
Controleer of de functie F: [0, ∞) R gedefinieerd door F (x) = 3xtwee het is injectief.
Dit keer is het domein van de uitdrukking al beperkt. Er wordt ook opgemerkt dat de waarden van de afhankelijke variabele zich in dit interval niet herhalen.
Daarom kan worden geconcludeerd dat F: [0, ∞) R gedefinieerd door F (x) = 3xtwee het is injectief
Voorbeeld 7
Bepaal welke van de volgende functies is
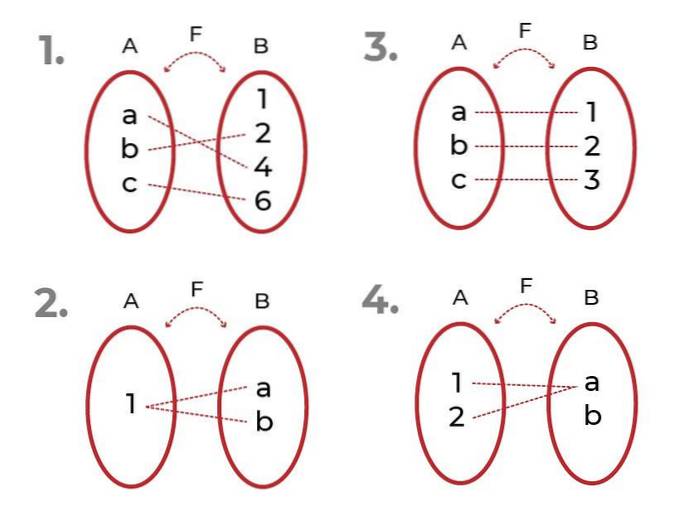
- Het is injectief. De bijbehorende elementen van het codomein zijn uniek voor elke waarde van de onafhankelijke variabele.
- Het is niet injectief. Er zijn elementen van het codomein geassocieerd met meer dan één element van de startset.
- Het is injectief
- Het is niet injectief
Voorgestelde oefeningen voor klas / thuis
Controleer of de volgende functies injectief zijn:
F: [0, ∞) → R gedefinieerd door F (x) = (x + 3)twee
F: [ π / 2,3π / 2 ] → R. gedefinieerd door F (x) = Geelbruin (x)
F: [ -π,π ] → R. gedefinieerd door F (x) = Cos (x + 1)
F: R R gedefinieerd door de lijn F (x) = 7x + 2
Referenties
- Inleiding tot logica en kritisch denken. Merrilee H. Salmon. Universiteit van Pittsburgh
- Problemen bij wiskundige analyse. Piotr Biler, Alfred Witkowski. Universiteit van Wroclaw. Polen.
- Elementen van abstracte analyse. Mícheál O'Searcoid PhD. Afdeling wiskunde. University college Dublin, Beldfield, Dublind 4.
- Inleiding tot de logica en de methodologie van de deductieve wetenschappen. Alfred Tarski, New York Oxford. Oxford Universiteit krant.
- Principes van wiskundige analyse. Enrique Linés Escardó. Redactioneel Reverté S. A 1991. Barcelona Spanje.



Niemand heeft nog op dit artikel gereageerd.