EEN surjectieve functie is elke relatie waarbij elk element dat tot het codomain behoort een afbeelding is van ten minste één element van het domein. Ook wel bekend als functie Aan, maken deel uit van de classificatie van functies met betrekking tot de manier waarop hun elementen met elkaar in verband staan.
Bijvoorbeeld een functie F: A B gedefinieerd door F (x) = 2x
Welke luidt "F. hoe zit het met NAAR tot B gedefinieerd door F (x) = 2x "
Het is tijd om de start- en eindsets te definiëren A en B.
A: 1, 2, 3, 4, 5 Nu zijn de waarden of afbeeldingen die elk van deze elementen zal tonen wanneer ze worden geëvalueerd in F., zullen de elementen van het codomain zijn.
F (1) = 2
F (2) = 4
F (3) = 6
F (4) = 8
F (5) = 10
Zo vormt het het geheel B: 2, 4, 6, 8, 10
Geconcludeerd kan dan worden dat:
F: 1, 2, 3, 4, 5 2, 4, 6, 8, 10 gedefinieerd door F (x) = 2x Het is een surjectieve functie
Elk element van het codomein moet het resultaat zijn van ten minste één bewerking van de onafhankelijke variabele via de betreffende functie. Er is geen beperking van afbeeldingen, een element van het codomain kan een afbeelding zijn van meer dan één element van het domein en er nog steeds een proberen surjectieve functie.
De afbeelding toont 2 voorbeelden met surjectieve functies.
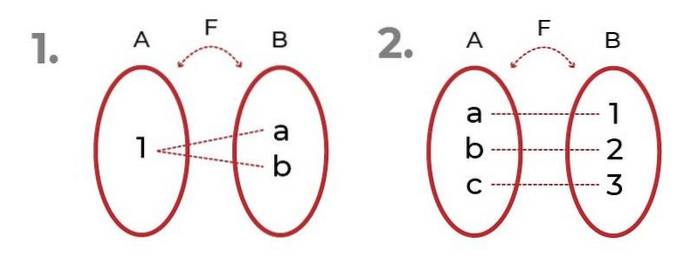
In het eerste wordt opgemerkt dat de afbeeldingen naar hetzelfde element kunnen worden verwezen, zonder de surjectiviteit van de functie.
In het tweede zien we een rechtvaardige verdeling tussen domein en afbeeldingen. Dit geeft aanleiding tot bijectieve functie, waar de criteria van injectieve functie en surjectieve functie.
Een andere identificatiemethode surjectieve functies, is om te controleren of het codomain gelijk is aan het bereik van de functie. Dit betekent dat als de aankomstreeks gelijk is aan de afbeeldingen die door de functie worden geleverd bij het evalueren van de onafhankelijke variabele, de functie is surjectief.
Artikel index
Overwegen surjectief voor een functie moet het volgende worden vervuld:
Worden F: DF. CF.
∀ b ℮ CF. EN tot ℮ DF. / F (a) = b
Dit is de algebraïsche manier om dat vast te stellen voor alle "b" die tot C behoortF. er is een "a" die toebehoort aan DF. zodanig dat de functie F geëvalueerd in "a" gelijk is aan "b".
Surjectiviteit is een eigenaardigheid van functies, waarbij het codomein en het bereik vergelijkbaar zijn. De elementen die in de functie worden geëvalueerd, vormen dus de aankomstset.
Soms een functie die dat niet is surjectief, het kan aan bepaalde voorwaarden worden onderworpen. Deze nieuwe voorwaarden kunnen er een surjectieve functie.
Allerlei wijzigingen aan het domein en codomain van de functie zijn geldig, waarbij het doel is om de surjectiviteitseigenschappen in de bijbehorende relatie te vervullen.
Om te voldoen aan de voorwaarden van surjectiviteit verschillende conditioneringstechnieken moeten worden toegepast, dit om ervoor te zorgen dat elk element van het codomain binnen de set afbeeldingen van de functie valt.
A: [Alle reële getallen]
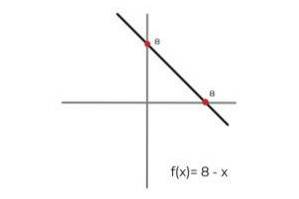
In dit geval beschrijft de functie een ononderbroken lijn die alle reële getallen in zowel het domein als het bereik omvat. Omdat het bereik van de functie RF. is gelijk aan codomain R Geconcludeerd kan worden dat:
F: R R gedefinieerd door de lijn F (x) = 8 - x is een surjectieve functie.
Dit geldt voor alle lineaire functies (functies waarvan de grootste graad van de variabele één is).
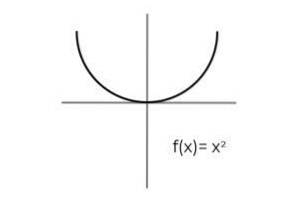
Het eerste dat u moet overwegen, is het codomain van F., die is opgebouwd uit de reële getallen R. De functie kan geen negatieve waarden retourneren, waardoor de echte negatieven van de mogelijke afbeeldingen worden uitgesloten.
Conditionering van het codomein aan het interval [0 , Het wordt vermeden om elementen van het codomain niet-gerelateerd te laten F..
De afbeeldingen worden herhaald voor paren elementen van de onafhankelijke variabele, zoals x = 1 Y x = - 1. Maar dit heeft alleen invloed op de injectiviteit van de functie, geen probleem voor deze studie.
Op deze manier kan worden geconcludeerd dat:
F: R [0, ∞ gedefinieerd door F (x) = xtwee Het is een surjectieve functie
F: R R gedefinieerd door F (x) = Sen (x)
F: R R gedefinieerd door F (x) = Cos (x)
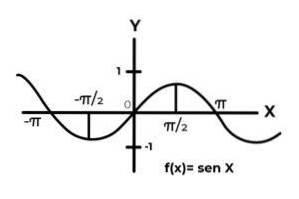
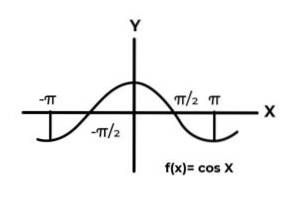
Het gedrag van de trigonometrische functies is vergelijkbaar met dat van golven, wat zeer gebruikelijk is om herhalingen van de afhankelijke variabele tussen de afbeeldingen te vinden. Ook is in de meeste gevallen het bereik van de functie beperkt tot een of meer sectoren van de reële lijn.
Dit is het geval voor de sinus- en cosinusfuncties. Waar hun waarden fluctueren in het interval [-1, 1]. Dit interval moet het codomain conditioneren om de surjectiviteit van de functie te bereiken.
F: R [-eleven] gedefinieerd door F (x) = Sen (x) Het is een surjectieve functie
F: R [-eleven]gedefinieerd door F (x) = Cos (x) Het is een surjectieve functie
F: [0, ∞ R gedefinieerd door F (x) = ± √x geef aan of het een surjectieve functie
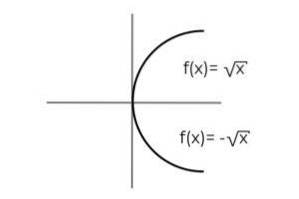
De functie F (x) = ± √x Het heeft de bijzonderheid dat het 2 afhankelijke variabelen definieert voor elke waarde van "x". Dat wil zeggen, de reeks ontvangt 2 elementen voor elke die in het domein is gemaakt. Voor elke waarde van ‘x’ moet een positieve en een negatieve waarde worden geverifieerd.
Bij het observeren van de startset wordt opgemerkt dat het domein al is beperkt, dit om de onbepaaldheden te vermijden die worden geproduceerd bij het evalueren van een negatief getal binnen een even wortel..
Bij het verifiëren van het bereik van de functie wordt opgemerkt dat elke waarde van het codomein tot het bereik behoort.
Op deze manier kan worden geconcludeerd dat:
F: [0, ∞ R gedefinieerd door F (x) = ± √x Het is een surjectieve functie
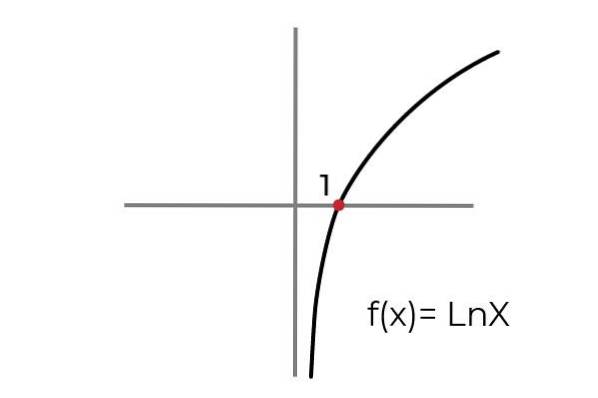
Zoals weergegeven in de grafiek is de functie F (x) = Ln xhet is gedefinieerd voor waarden van "x" groter dan nul. Terwijl de waarden van "en" of de afbeeldingen elke echte waarde kunnen aannemen.
Op deze manier kunnen we het domein van F (x) = tot interval (0 ,
Zolang het bereik van de functie kan worden behouden als de reeks reële getallen R.
Gezien dit, kan worden geconcludeerd dat:
F: [0, ∞ R gedefinieerd door F (x) = Ln x Het is een surjectieve functie
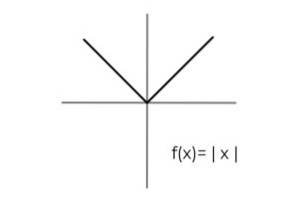
Het domein van de functie geldt voor alle reële getallen R. Op deze manier moet de enige conditionering worden uitgevoerd in het codomain, rekening houdend met het feit dat de functie absolute waarde alleen positieve waarden aanneemt..
We gaan verder met het vaststellen van het codomain van de functie door het gelijk te stellen aan de rang van dezelfde
[0 ,
Nu kan worden geconcludeerd dat:
F: [0, ∞ R gedefinieerd door F (x) = | x | Het is een surjectieve functie
Niemand heeft nog op dit artikel gereageerd.