
Multiplicatieve inverse uitleg, voorbeelden, opgeloste oefeningen
Het wordt begrepen door Inverse multiplicatief van een getal, een ander getal dat vermenigvuldigd wordt met het eerste, geeft als resultaat het neutrale element van het product, dat wil zeggen de eenheid. Als je een echt nummer hebt naar dan wordt zijn multiplicatieve inverse aangeduid met naar-1, en het is waar dat:
een een-1 = een-1 a = 1
Meestal het nummer naar behoort tot een reeks reële getallen.
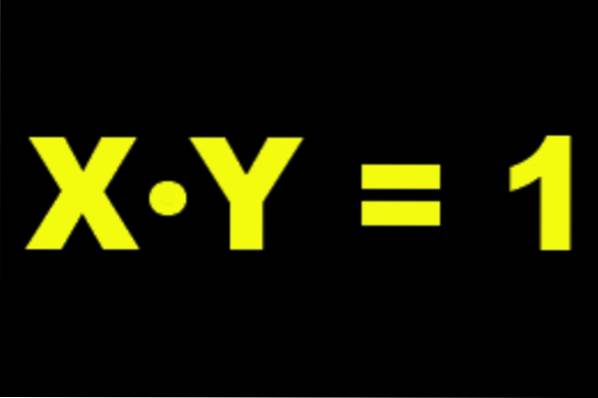
Als we bijvoorbeeld nemen a = 2, dan is zijn multiplicatieve inverse twee-1 = ½ aangezien het volgende is geverifieerd:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2⋅ ½ = ½ ⋅ 2 = 1
Naar de Inverse multiplicatief van een nummer wordt ook wel de wederkerig, omdat de multiplicatieve inverse wordt verkregen door teller en noemer uit te wisselen, bijvoorbeeld de multiplicatieve inverse van 3/4 is 4/3.
Als algemene regel kan worden gesteld dat voor een rationaal getal (p / q) zijn multiplicatieve inverse (p / q)-1 Het is wederkerig (q / p) zoals hieronder kan worden geverifieerd:
(p / q) ⋅ (p / q)-1 = (p / q) ⋅ (q / p) = (p⋅ q) / (q⋅ p) = (p⋅ q) / (p⋅ q) = 1
De multiplicatieve inverse bestaat niet in de numerieke set van gehele getallen, Als bijvoorbeeld het gehele getal 2 wordt genomen, is de vermenigvuldigende inverse volgens wat hierboven is gezien ½, maar een ½ is geen geheel getal..
Er is ook geen multiplicatieve inverse van het nul-element van vermenigvuldiging. Met andere woorden, het getal nul (0), dat het nulelement is van de vermenigvuldigingsbewerking, heeft geen multiplicatieve inverse, aangezien er geen getal is dat wordt vermenigvuldigd met de eenheid nul.
De multiplicatieve inverse bestaat in rationale getallen, in reële getallen en in complexe getallen.
Voorbeelden van multiplicatieve inverse
voorbeeld 1
Zoek de multiplicatieve inverse van 3/2 en controleer of deze voldoet aan de eigenschap van vermenigvuldigende gehele getallen.
Volgens de bovenstaande regel worden de teller en de noemer op deze manier verwisseld, de multiplicatieve inverse van (3/2) is (2/3). Om de vermenigvuldiging van de twee getallen te verifiëren, wordt uitgevoerd:
(3/2) ⋅ (2/3) = (3 ⋅ 2) / (2 ⋅ 3) = 6/6 = 1.
Om twee fractionele getallen te vermenigvuldigen, vermenigvuldigt u eenvoudig de teller van de eerste met de teller van de tweede om de teller van het resultaat te krijgen..
Om de noemer van een product van fractionele getallen te verkrijgen, gaat u op dezelfde manier te werk, dat wil zeggen, vermenigvuldigt u de noemers met elkaar en het resultaat is de noemer van het product. In ons voorbeeld is geverifieerd dat de teller van het product van het getal en het omgekeerde ervan 6 is en de noemer 6, waardoor de breuk 6/6 overblijft die 1 is.
Voorbeeld 2
De multiplicatieve inverse van -5 moet niet worden verward met zijn symmetrische (+5) die soms de rekenkundige inverse wordt genoemd. De multiplicatieve inverse wordt als volgt verkregen:
(-5) ⋅ X = 1
Waar X de multiplicatieve inverse is die moet worden verkregen. Een mogelijke procedure is om de onbekende X op te lossen. Aangezien (-5) de onbekende X in het linker lid vermenigvuldigt, gebeurt het dat het rechter lid wordt gedeeld:
X = 1 / (-5)
Omdat bekend is dat + tussen - is -, wordt uiteindelijk X verkregen:
X = - ⅕ .
Concluderend - ⅕ is de multiplicatieve inverse van -5.
Voorbeeld 3
Bereken de multiplicatieve inverse van -√2. Stel dat de multiplicatieve inverse X is, dan moet -√2 vermenigvuldigd met X eenheid zijn, een voorwaarde die we hieronder stellen:
-√2 ⋅ X = 1
Vervolgens worden beide leden gedeeld door -√2 om te krijgen:
(-√2 ⋅ X) / (-√2) = 1 / (-√2)
In het eerste lid wordt -√2 vereenvoudigd, waardoor:
X = 1 / (-√2)
Deze uitdrukking kan worden gerationaliseerd, dat wil zeggen, elimineer de wortel van de noemer, vermenigvuldig de teller met (-√2) en in de noemer met hetzelfde bedrag, zodat het resultaat niet wordt gewijzigd:
X = (-√2) / [(-√2) (- √2)] = - (√2 / 2)
Concluderend - (√2 / 2) is de multiplicatieve inverse van (-√2).
Voorbeeld 4
Veronderstel een willekeurig getal x, verkrijg zijn multiplicatieve inverse en geef het grafisch weer.
In dit geval is het een functie f (x) = x, het verkrijgen van de multiplicatieve inverse is het vinden van de functie g (x) zodanig dat vermenigvuldigd met het eerste getal van de eenheid. De functie g is het omgekeerde van f en moet op geen enkele manier worden verward met zijn inverse functie.
Met andere woorden, de multiplicatieve inverse van x is een y zodat het volgende waar is:
x ⋅ y = 1
vanwaar clearing en je hebt:
y = 1 / x.
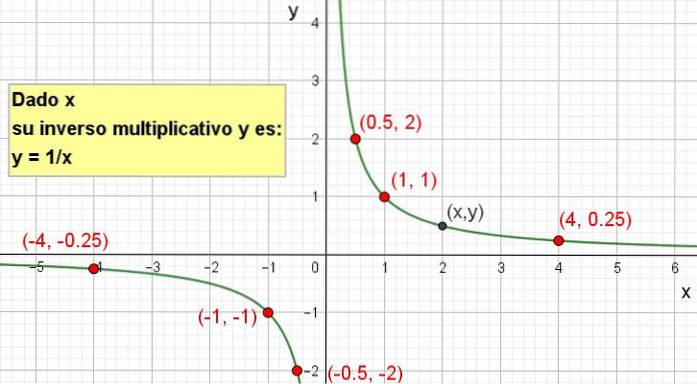
Het bovenstaande wordt aldus geïnterpreteerd als de waarde x wordt gegeven, de vorige formule geeft ons zijn multiplicatieve inverse.
Het is mogelijk om de grafische weergave te maken zoals weergegeven in de volgende afbeelding:
Opleiding
Oefening 1
Gegeven x = 2 - √2, verkrijg zijn multiplicatieve inverse y.
Oplossing:
Om y een multiplicatieve inverse van x te laten zijn, moet aan de volgende gelijkheid zijn voldaan:
x ⋅ y = 1
Vervang x door zijn waarde:
(2 - √2) ⋅ y = 1
Dan wordt het gewist en:
y = 1 / (2 - √2)
Om het resultaat te rationaliseren, worden de teller en de noemer vermenigvuldigd met hun geconjugeerde binominale waarde:
y = (2 + √2) / ((2 + √2) (2 - √2))
In de noemer wordt een opmerkelijk product herkend dat het product van een som en een verschil wordt genoemd, het verschil tussen de kwadraten. Op deze manier verdwijnt de wortel in de noemer.
y = (2 + √2) / (2 ^ 2 - (√2) ^ 2)
De bevoegdheden oplossen:
y = (2 + √2) / (4 - 2)
Vereenvoudigen:
y = (2 + √2) / 2
Oefening 2
Verkrijg de multiplicatieve inverse van (1 / a + 1 / b) waarbij a en b niet nul reële getallen zijn.
Oplossing:
We noemen Y de multiplicatieve inverse van (1 / a + 1 / b), dus aan de volgende vergelijking moet worden voldaan:
En ⋅ (1 / a + 1 / b) = 1
De variabele Y wordt gewist:
Y = 1 / (1 / een + 1 / b)
De noemer is opgelost:
Y = 1 / ((b + a) / een b)
Zoals bekend uit de regels van de algebra, gaat de noemer van de noemer over naar de teller:
Y = (een b) / (b + a)
Het wordt bevolen om uiteindelijk te verkrijgen:
(a b) / (a + b) wat de multiplicatieve inverse is van (1 / a + 1 / b).
Oefening 3
Verkrijg de multiplicatieve inverse van (a - b) / (a ^ 2 - b ^ 2).
Oplossing:
Onthoud dat de multiplicatieve inverse ook wel de reciproque wordt genoemd, omdat deze precies wordt verkregen door teller en noemer uit te wisselen.
Dan is de multiplicatieve inverse van (a - b) / (a ^ 2 - b ^ 2):
(a ^ 2 - b ^ 2) / (a - b)
Maar deze uitdrukking kan worden vereenvoudigd als we erkennen, volgens de regels van de algebra, dat de teller een verschil van kwadraten is dat kan worden meegerekend als het product van een som door een verschil:
((a + b) (a - b)) / (a - b)
Omdat er een gemeenschappelijke factor (a - b) is in de teller en in de noemer, gaan we verder met vereenvoudigen en krijgen we uiteindelijk:
(a + b) wat de multiplicatieve inverse is van (a - b) / (a ^ 2 - b ^ 2).
Referenties
- Fuentes, A. (2016). BASIS WISKUNDE. Een inleiding tot calculus. Lulu.com.
- Garo, M. (2014). Wiskunde: kwadratische vergelijkingen: hoe een kwadratische vergelijking op te lossen. Marilù Garo.
- Haeussler, E. F., en Paul, R. S. (2003). Wiskunde voor management en economie. Pearson Education.
- Jiménez, J., Rofríguez, M., & Estrada, R. (2005). Wiskunde 1 SEP. Drempel.
- Preciado, C. T. (2005). Wiskundecursus 3e. Redactioneel Progreso.
- Rock, N. M. (2006). Algebra I is gemakkelijk! Zo makkelijk. Team Rock Press.
- Sullivan, J. (2006). Algebra en trigonometrie. Pearson Education.



Niemand heeft nog op dit artikel gereageerd.