
De 10 belangrijkste kenmerken van het plein
Kenmerkend voor het centrale plein is dat het uit vier zijden bestaat, die exact dezelfde afmetingen hebben. Deze zijkanten zijn gerangschikt om vier rechte hoeken (90 °) te vormen.
De plein Het is een geometrische basisfiguur, object van studie van de vlakke geometrie, aangezien het een tweedimensionale figuur is (die breedte en hoogte heeft maar diepte mist).

De vierkanten zijn polygonen. Meer specifiek zijn polygonen (a) vierhoekig omdat ze vier zijden hebben, (b) gelijkzijdig omdat ze zijden hebben die hetzelfde meten, en (c) gelijke hoeken omdat ze hoeken hebben met dezelfde amplitude..
Deze laatste twee eigenschappen van het vierkant (gelijkzijdig en gelijkhoekig) kunnen in één woord worden samengevat: normaal. Dit betekent dat de vierkanten regelmatige vierhoekige polygonen zijn.
Net als andere geometrische figuren heeft het vierkant een oppervlakte. Dit kan worden berekend door een van de zijden met zichzelf te vermenigvuldigen. Als we bijvoorbeeld een vierkant hebben van 4 mm, is de oppervlakte 16 mmtwee.
Vierkanten opvallende kenmerken
1- Aantal zijden en afmeting
De vierkanten bestaan uit vier zijden die hetzelfde meten. Vierkanten zijn ook tweedimensionale figuren, wat betekent dat ze maar twee afmetingen hebben: breedte en hoogte..
Het basiskenmerk van vierkanten is dat ze vier zijden hebben. Het zijn platte figuren, dus ze worden tweedimensionaal genoemd.
2- Veelhoek
De vierkanten zijn een veelhoek. Dit betekent dat de vierkanten geometrische figuren zijn die worden begrensd door een gesloten lijn gevormd door opeenvolgende lijnsegmenten (gesloten veelhoekige lijn).
Concreet is het een vierzijdige veelhoek omdat het vier zijden heeft.
3- gelijkzijdige veelhoek
Een polygoon is gelijkzijdig als alle zijden dezelfde maat hebben. Dit betekent dat als een van de zijden van het plein 2 meter meet, alle zijden 2 meter lang zijn..
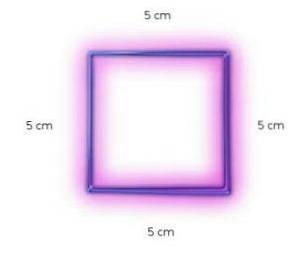
De vierkanten zijn gelijkzijdig, wat betekent dat al hun zijden hetzelfde meten.
In de afbeelding is een vierkant met gelijke zijden van 5 cm weergegeven.
4- Gelijkhoekige veelhoek
Van een veelhoek wordt gezegd dat deze gelijkhoekig is als alle hoeken die door de gesloten veelhoekige lijn worden gevormd, dezelfde afmeting hebben.
Alle vierkanten zijn opgebouwd uit vier rechte hoeken (d.w.z. hoeken van 90 °), ongeacht de specifieke hoekmetingen: zowel een vierkant van 2 cm x 2 cm als een vierkant van 10 m x 10 m hebben vier rechte hoeken.
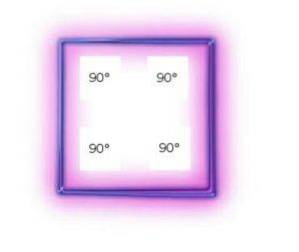
Alle vierkanten zijn gelijkhoeken omdat hun hoeken dezelfde amplitude hebben. Dat wil zeggen 90 °.
5- Regelmatige veelhoek
Wanneer een veelhoek zowel gelijkzijdig als gelijkhoekig is, wordt deze beschouwd als een regelmatige veelhoek.
Omdat het vierkant zijden heeft die dezelfde meten en hoeken van gelijke amplitude, kan worden gezegd dat dit een regelmatige veelhoek is.
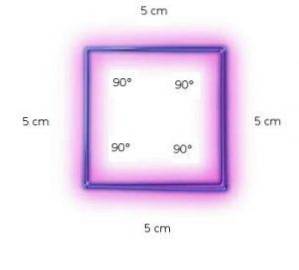
Vierkanten hebben beide zijden van gelijke afmetingen en hoeken van gelijke breedte, dus het zijn regelmatige polygonen.
In de bovenstaande afbeelding is een vierkant met vier zijden van 5 cm en vier hoeken van 90 ° weergegeven.
6- De oppervlakte van een vierkant
De oppervlakte van een vierkant is gelijk aan het product van de ene zijde en de andere zijde. Omdat de twee zijden exact dezelfde maat hebben, kan de formule worden vereenvoudigd door te zeggen dat de oppervlakte van deze polygoon gelijk is aan een van de zijden in het kwadraat, dat wil zeggen (zijde)twee.
Enkele voorbeelden van het berekenen van de oppervlakte van een vierkant zijn:
- Vierkant met zijden van 2 m: 2 m x 2 m = 4 mtwee
- Vierkanten met zijkanten van 52 cm: 52 cm x 52 cm = 2704 cmtwee
- Vierkant met zijkanten van 10 mm: 10 mm x 10 mm = 100 mmtwee
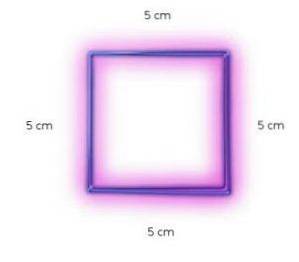
Het vierkant op de afbeelding heeft zijden van 5 cm.
Het gebied is het product van 5 cm x 5 cm, of wat hetzelfde is (5 cm)twee
In dit geval is de oppervlakte van het vierkant 25 cmtwee
7- Vierkanten zijn parallellogrammen
Parallellogrammen zijn een soort vierhoek met twee paar parallelle zijden. Dit betekent dat het ene paar zijden naar elkaar is gericht, terwijl hetzelfde gebeurt met het andere paar..
Er zijn vier soorten parallellogrammen: rechthoeken, ruiten, romboïden en vierkanten..
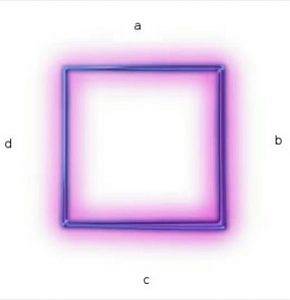
Vierkanten zijn parallellogrammen omdat ze twee paar zijden hebben die evenwijdig zijn..
Zijden (a) en (c) zijn parallel.
Zijden (b) en (d) zijn parallel.
8- De tegenovergestelde hoeken zijn congruent en de opeenvolgende zijn complementair
Dat twee hoeken congruent zijn, betekent dat ze dezelfde amplitude hebben. In die zin kan, aangezien een vierkant alle hoeken van dezelfde amplitude heeft, worden gezegd dat de tegenovergestelde hoeken congruent zijn.
Aan de andere kant betekent het feit dat twee opeenvolgende hoeken complementair zijn, dat de som van deze twee gelijk is aan een rechte hoek (degene met een amplitude van 180 °).
De hoeken van een vierkant zijn rechte hoeken (90 °), dus hun som geeft 180 °.
9- Ze zijn gebouwd vanuit een omtrek
Om een vierkant te construeren, wordt een cirkel getekend. Op deze omtrek worden vervolgens twee diameters getekend; deze diameters moeten loodrecht staan en een kruis vormen.
Zodra de diameters zijn getekend, hebben we vier punten waar de lijnsegmenten de omtrek snijden. Als deze vier punten worden samengevoegd, is het resultaat een vierkant.
10- De diagonalen snijden elkaar in het midden
Diagonalen zijn rechte lijnen die van de ene hoek naar de andere worden getrokken, die tegenovergesteld is. In een vierkant kunnen twee diagonalen worden getekend. Deze diagonalen kruisen elkaar in het midden van het vierkant.
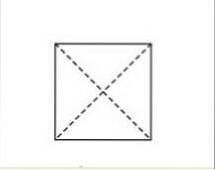
In de afbeelding stellen de stippellijnen de diagonalen voor. Zoals u kunt zien, snijden deze lijnen elkaar precies in het midden van het vierkant..
Referenties
- Plein. Opgehaald op 17 juli 2017, via en.wikipedia.org
- Vierkant en zijn eigenschappen. Opgehaald op 17 juli 2017, van mathonpenref.com
- Eigenschappen van ruiten, rechthoeken en vierkanten. Opgehaald op 17 juli 2017, via dummies.com
- De eigenschappen van een vierkant. Opgehaald op 17 juli 2017, via coolmth.com
- Plein. Opgehaald op 17 juli 2017, via onlinemschool.com
- Eigenschappen van vierkanten. Opgehaald op 17 juli 2017, via brlliant.org.



Niemand heeft nog op dit artikel gereageerd.