
Charles Law formules en eenheden, experiment, oefeningen
De Charles Law of Guy-Lussac is er een die de verklaring van een van de eigenschappen van de gasvormige toestand mogelijk maakt: het volume dat een gas inneemt, is recht evenredig met de temperatuur bij constante druk.
Deze proportionaliteit is lineair voor alle temperatuurbereiken als het gas in kwestie ideaal is; echte gassen wijken daarentegen af van de lineaire trend bij temperaturen in de buurt van hun dauwpunt. Dit heeft het gebruik van deze wet echter niet beperkt voor een groot aantal toepassingen met gassen..

Een van de typische toepassingen van de wet van Charles is in luchtballonnen. Andere eenvoudigere ballonnen, zoals die van wensen, ook wel Chinese lantaarns genoemd (bovenste afbeelding), onthullen de relatie tussen het volume en de temperatuur van een gas bij constante druk.
Waarom bij constante druk? Want als de druk zou toenemen, zou dit betekenen dat de container waarin het gas zich bevindt hermetisch gesloten is; en hiermee zouden de botsingen of stoten van de gasvormige deeltjes tegen de binnenwanden van de container toenemen (wet van Boyle-Mariotte).
Daarom zou er geen verandering zijn in het volume dat door het gas wordt ingenomen, en de wet van Charles zou ontbreken. In tegenstelling tot een luchtdichte container, vertegenwoordigt het weefsel van de wensballonnen een mobiele barrière, die kan uitzetten of krimpen afhankelijk van de druk die wordt uitgeoefend door het gas binnenin..
Naarmate het weefsel van de ballonnen echter uitzet, blijft de inwendige druk van het gas constant omdat het gebied waarover de deeltjes botsen toeneemt. Hoe hoger de gastemperatuur, hoe hoger de kinetische energie van de deeltjes, en dus het aantal botsingen.
En terwijl de ballon weer uitzet, blijven de botsingen tegen de binnenwanden (idealiter) constant..
Dus hoe heter het gas, hoe groter de uitzetting van de ballon en hoe hoger hij zal stijgen. Het resultaat: roodachtige (hoewel gevaarlijke) lichten die in decemberavonden in de lucht hangen..
Artikel index
- 1 Wat is de wet van Charles?
- 1.1 Verklaring
- 1.2 Banen
- 1.3 Grafiek
- 2 Formules en meeteenheden
- 2.1 Formules
- 2.2 Eenheden
- 3 Experimenteer om de wet te bewijzen
- 3.1 Montage
- 3.2 Ontwikkeling
- 3.3 Ballon met ijs in de winter
- 4 Opgeloste oefeningen
- 4.1 Oefening 1
- 4.2 Oefening 2
- 4.3 Oefening 3
- 5 Toepassingen
- 5.1 Ballonnen van wensen
- 5.2 Pop-up- of kalkoen-thermometers
- 5.3 De vorm van de pingpongballen herstellen
- 5.4 Bereiding van de broden
- 6 referenties
Wat is de wet van Charles?
Uitspraak
De zogenaamde Charles-wet of de wet van Gay-Lussac verklaart de afhankelijkheid die bestaat tussen het volume dat door een gas wordt ingenomen en de waarde van de absolute temperatuur of Kelvin-temperatuur..
De wet kan als volgt worden geformuleerd: als de druk constant blijft, volgt daaruit dat “voor een gegeven massa van een gas, het zijn volume toeneemt met ongeveer 1/273 keer zijn volume bij 0 ºC, voor elke graad Celsius (1 ºC) om de temperatuur te verhogen ".
Jobs
Het onderzoekswerk dat de wet tot stand bracht, werd in de jaren 1780 gestart door Jacques Alexander Cesar Charles (1746-1823). Charles heeft de resultaten van zijn onderzoek echter niet gepubliceerd..
Later slaagde John Dalton er in 1801 in om experimenteel vast te stellen dat alle gassen en dampen, die hij bestudeerde, uitzetten tussen twee bepaalde temperaturen in dezelfde volumehoeveelheid. Deze resultaten werden in het jaar 1802 door Gay-Lussac bevestigd.
De onderzoekswerken van Charles, Dalton en Gay-Lussac hebben aangetoond dat het volume dat door een gas wordt ingenomen en de absolute temperatuur ervan recht evenredig zijn. Daarom is er een lineaire relatie tussen de temperatuur en het volume van een gas.
Grafiek
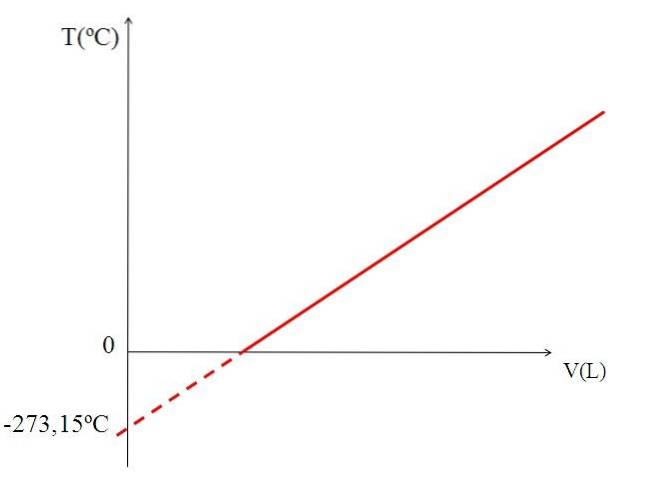
Grafiek (bovenste afbeelding) het volume van een gas versus temperatuur levert een rechte lijn op. Het snijpunt van de lijn met de X-as, bij een temperatuur van 0 ºC, maakt het mogelijk om het volume van het gas bij 0 ºC te verkrijgen.
Evenzo zou het snijpunt van de lijn met de X-as informatie geven over de temperatuur waarvoor het door het gas ingenomen volume nul "0" zou zijn. Dalton schatte deze waarde op -266 ºC, dichtbij de door Kelvin voorgestelde waarde voor het absolute nulpunt (0).
Kelvin stelde een temperatuurschaal voor waarvan het nulpunt de temperatuur zou moeten zijn waarbij een perfect gas een volume van nul zou hebben. Maar bij deze lage temperaturen worden de gassen vloeibaar gemaakt.
Daarom is het niet mogelijk om als zodanig van gassenvolumes te spreken, waarbij wordt vastgesteld dat de waarde voor het absolute nulpunt -273,15 ºC moet zijn.
Formules en meeteenheden
Formules
De wet van Charles in zijn moderne versie stelt dat het volume en de temperatuur van een gas recht evenredig zijn.
Dan:
V / T = k
V = gasvolume. T = Kelvin-temperatuur (K). k = evenredigheidsconstante.
Voor een volume V1 en een temperatuur T1
k = V1 / T1
Evenzo voor een volume Vtwee en een temperatuur Ttwee
k = Vtwee / Ttwee
Vervolgens stellen we de twee vergelijkingen voor k gelijk
V.1 / T1 = Vtwee / Ttwee
Deze formule kan als volgt worden geschreven:
V.1 Ttwee = Vtwee T1
Oplossen voor Vtwee, je krijgt de formule:
V.twee = V1 Ttwee / T1
Eenheden
Het volume van het gas kan worden uitgedrukt in liters of in een van de daarvan afgeleide eenheden. Evenzo kan het volume worden uitgedrukt in kubieke meter of in een afgeleide eenheid. De temperatuur moet worden uitgedrukt in absolute temperatuur of Kelvin-temperatuur.
Dus als de temperaturen van een gas worden uitgedrukt in graden Celsius of de schaal van Celsius, om er een berekening mee uit te voeren, zou het bedrag van 273,15 ºC bij de temperaturen moeten worden opgeteld om ze op absolute temperaturen of Kelvin te brengen..
Als de temperaturen worden uitgedrukt in graden Fahrenheit, zou het nodig zijn om 459,67 ºR aan die temperaturen toe te voegen om ze op absolute temperaturen op de Rankine-schaal te brengen..
Een andere bekende formule van de wet van Charles, die rechtstreeks verband houdt met de bewering ervan, is de volgende:
V.t = Vof (1 + t / 273)
Waar Vt is het volume dat wordt ingenomen door een gas bij een bepaalde temperatuur, uitgedrukt in liter, cm3, enz.; en Vof is het volume dat wordt ingenomen door een gas bij 0 ºC. Van zijn kant is t de temperatuur waarbij het volume wordt gemeten, uitgedrukt in graden Celsius (ºC).
En tot slot vertegenwoordigt 273 de waarde van het absolute nulpunt op de temperatuurschaal van Kelvin.
Experimenteer om de wet te bewijzen
Montage
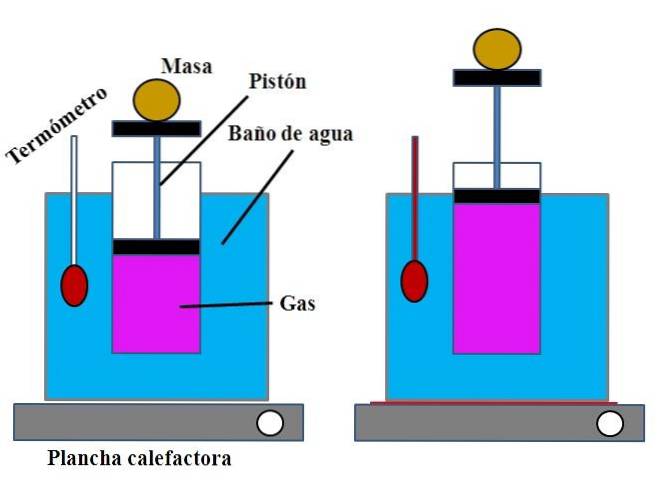
In een bak met water, die de functie van een waterbad vervulde, werd bovenaan een open cilinder geplaatst met een plunjer die op de binnenwand van de cilinder paste (afbeelding boven).
Deze zuiger (bestaande uit de zuiger en de twee zwarte bases) zou naar de boven- of onderkant van de cilinder kunnen bewegen, afhankelijk van het gasvolume dat erin zat..
Het waterbad kon worden verwarmd door een brander of verwarmingsinstallatie te gebruiken, die de nodige warmte leverde om de temperatuur van het bad en daarmee de temperatuur van de cilinder uitgerust met een zuiger te verhogen..
Een bepaalde massa werd op de plunjer geplaatst om er zeker van te zijn dat het experiment onder constante druk werd uitgevoerd. De temperatuur van het bad en de cilinder werd gemeten met behulp van een thermometer die in het waterbad was geplaatst..
Hoewel de cilinder waarschijnlijk geen schaalverdeling had om het luchtvolume te visualiseren, kon dit worden geschat door de hoogte te meten die werd bereikt door de massa op de zuiger en het oppervlak van de basis van de cilinder..
Ontwikkelen
Het volume van een cilinder wordt verkregen door het oppervlak van de basis te vermenigvuldigen met de hoogte. Het oppervlak van de cilinderbasis kan worden verkregen door de formule toe te passen: S = Pi x rtwee.
Terwijl de hoogte wordt verkregen door de afstand te meten van de basis van de cilinder tot het deel van de zuiger waarop de massa rust.
Naarmate de temperatuur van het bad werd verhoogd door de warmte die door de aansteker werd geproduceerd, werd waargenomen dat de plunjer in de cilinder steeg. Vervolgens lazen ze op de thermometer de temperatuur in het waterbad af, die overeenkwam met de temperatuur in de cilinder..
Evenzo maten ze de hoogte van de massa boven de plunjer, waardoor ze het luchtvolume konden schatten dat overeenkwam met de gemeten temperatuur. Op deze manier hebben ze verschillende temperatuurmetingen gedaan en schattingen van het luchtvolume dat overeenkomt met elk van de temperaturen..
Hiermee kon eindelijk worden vastgesteld dat het volume dat een gas inneemt recht evenredig is met zijn temperatuur. Deze conclusie maakte het mogelijk om de zogenaamde wet van Charles uit te spreken.
Ballon met ijs in de winter
Naast het vorige experiment is er een eenvoudigere en meer kwalitatieve: die van de ballon met ijs in de winter..
Als een met helium gevulde ballon in de winter in een verwarmde kamer zou worden geplaatst, zou de ballon een bepaald volume hebben; Maar als het later met een lage temperatuur naar de buitenkant van het huis zou worden verplaatst, zou worden opgemerkt dat de heliumballon krimpt, waardoor het volume afneemt volgens de wet van Charles.
Opgeloste oefeningen
Oefening 1
Er is een gas dat een inhoud van 750 cm inneemt3 bij 25 ºC: welk volume neemt dit gas in bij 37 ºC als de druk constant wordt gehouden?
Het is noodzakelijk om eerst de temperatuureenheden naar Kelvin te transformeren:
T1 in Kelvin graden = 25 ºC + 273,15 ºC = 298,15 K
Ttwee in Kelvin graden = 37 ºC + 273,15 ºC = 310,15 K
Omdat V1 en de andere variabelen lossen we op voor Vtwee en wordt berekend met de volgende vergelijking:
V.twee = V1 · (T.twee / T1
= 750 cm3 · (310,15 K / 298,15 K)
= 780,86 cm3
Oefening 2
Wat zou de temperatuur in graden Celsius zijn waartoe 3 liter van een gas verwarmd zou moeten worden tot 32 ºC, zodat het volume uitzet tot 3,2 liter?
Nogmaals, de graden Celsius wordt omgezet in Kelvin:
T1 = 32 ºC + 273,15 ºC = 305,15 K
En net als in de vorige oefening, wordt T gewisttwee in plaats van Vtwee, en wordt hieronder berekend:
Ttwee = Vtwee · (T.1 / V1
= 3,2 L · (305,15 K / 3 L)
= 325,49 K.
Maar de verklaring vraagt om graden Celsius, dus de eenheid van T wordt gewijzigdtwee
Ttwee in graden Celsius = 325, 49 º C (K) - 273,15 ºC (K)
= 52,34 ºC
Oefening 3
Als een gas van 0 ºC een volume van 50 cm inneemt3, Welk volume zal het innemen bij 45 ºC?
Gebruikmakend van de originele formule van de wet van Charles:
V.t = Vof (1 + t / 273)
We gaan verder met het berekenen van Vt direct aangezien alle variabelen beschikbaar zijn:
V.t = 50 cm3 + 50 cm3 · (45 ºC / 273 ºC (K))
= 58,24 cm3
Aan de andere kant, als het probleem wordt opgelost met behulp van de strategie van voorbeelden 1 en 2, hebben we:
V.twee = V1 · (T.twee / T1
= 318 K · (50 cm3 / 273 K)
= 58,24 cm3
Het resultaat bij toepassing van de twee procedures is hetzelfde omdat ze uiteindelijk gebaseerd zijn op hetzelfde principe van de wet van Karel.
Toepassingen
Wens ballonnen
De wensballonnen (al genoemd in de inleiding) zijn voorzien van een textielmateriaal geïmpregneerd met een brandbare vloeistof.
Wanneer dit materiaal in brand wordt gestoken, neemt de temperatuur van de lucht in de ballon toe, waardoor het volume van het gas volgens de wet van Charles toeneemt..
Daarom, door het luchtvolume in de ballon te vergroten, neemt de dichtheid van de lucht erin af, wat minder wordt dan de dichtheid van de omringende lucht, en daarom stijgt de ballon.
Pop-up- of kalkoen-thermometers
Zoals hun naam al aangeeft, worden ze gebruikt bij het koken van kalkoenen. De thermometer heeft een met lucht gevulde houder afgesloten met een deksel en is zo gekalibreerd dat wanneer de optimale kooktemperatuur bereikt is, het deksel omhoog gaat en een geluid uitbrengt..
De thermometer wordt in de kalkoen geplaatst en naarmate de temperatuur in de oven toeneemt, zet de lucht in de thermometer uit, waardoor het volume toeneemt. Wanneer het volume van de lucht een bepaalde waarde bereikt, tilt u het deksel van de thermometer op.
De vorm van pingpongballen herstellen
Afhankelijk van de vereisten van hun gebruik, zijn de pingpongballen licht van gewicht en zijn hun plastic wanden dun. Dit zorgt ervoor dat wanneer ze worden geraakt door de rackets, ze vervormd raken.
Door de vervormde ballen in heet water te plaatsen, warmt de lucht binnenin op en zet uit, waardoor het luchtvolume toeneemt. Dit zorgt er ook voor dat de wand van de pingpongballen uitrekt, waardoor ze terugkeren naar hun oorspronkelijke vorm..
Brood maken
Gisten worden verwerkt in tarwebloem dat wordt gebruikt om brood te maken en hebben het vermogen om koolstofdioxidegas te produceren..
Naarmate de temperatuur van de broden toeneemt tijdens het koken, neemt het volume koolstofdioxide toe. Hierdoor zet het brood uit tot het het gewenste volume bereikt..
Referenties
- Clark J. (2013). Andere gaswetten - de wet van Boyle en de wet van Charles. Hersteld van: chemguide.co.uk
- Staroscik Andrew. (2018). Charles 'wet. Hersteld van: scienceprimer.com
- Wikipedia. (2019). Charles Law. Hersteld van: en.wikipedia.org
- Helmenstine, Todd. (27 december 2018). Wat is de formule voor de wet van Charles? Hersteld van: thoughtco.com
- Prof. N. De Leon. (s.f.). Elementaire gaswetten: Charles Law. C 101 Class Notes. Hersteld van: iun.edu
- Briceño Gabriela. (2018). Charles Law. Hersteld van: euston96.com
- Morris, J. G. (1974). Fysicochemie voor biologen. (tweegeeft editie). Redactioneel Reverté, S.A.


Niemand heeft nog op dit artikel gereageerd.