Metingen van centrale tendens voor gegroepeerde gegevensformules, oefeningen

De trend maatregelen centraal ze geven de waarde aan waarrond de gegevens van een distributie zich bevinden. De bekendste is het gemiddelde of rekenkundig gemiddelde, dat bestaat uit het optellen van alle waarden en het resultaat delen door het totale aantal gegevens.

Als de verdeling echter uit een groot aantal waarden bestaat en ze niet op een geordende manier worden gepresenteerd, is het niet eenvoudig om de nodige berekeningen uit te voeren om de waardevolle informatie die ze bevatten te extraheren..

Daarom zijn ze gegroepeerd in klassen of categorieën om een distributie van frequenties. Door deze eerdere ordening van de gegevens uit te voeren, is het gemakkelijker om de maten van centrale tendens te berekenen, waaronder:

-Voor de helft

-Mediaan

-mode

-Geometrisch gemiddelde

-Harmonisch gemiddelde

Formules

Hier zijn de formules voor de metingen van centrale tendens voor de gegroepeerde gegevens:

Rekenkundig gemiddelde

Het gemiddelde wordt het meest gebruikt om kwantitatieve gegevens (numerieke waarden) te karakteriseren, hoewel het vrij gevoelig is voor de extreme waarden van de verdeling. Het wordt berekend door:

Met:

-X: gemiddelde of rekenkundig gemiddelde

-F._ik: klasse frequentie

-m_ik: het klassenteken

-g: aantal klassen

-n: totale gegevens

Mediaan

Om het te berekenen, is het nodig om het interval te vinden dat de waarneming n / 2 bevat en te interpoleren om de numerieke waarde van die waarneming te bepalen, met behulp van de volgende formule:

Waar:

-c: breedte van het interval waartoe de mediaan behoort

-B._M.: ondergrens van genoemd interval

-F._m: aantal waarnemingen in het interval

-n / 2: totale gegevens gedeeld door 2.

-F._BM: aantal waarnemingen voordat van het interval dat de mediaan bevat.

Daarom is de mediaan een maatstaf voor de positie, dat wil zeggen dat het de gegevensset in twee delen verdeelt. Ze kunnen ook worden gedefinieerd kwartielen, decielen Y percentielen, die de verdeling verdelen in respectievelijk vier, tien en honderd delen.

mode

In de gepoolde gegevens wordt de klasse of categorie met de meeste waarnemingen doorzocht. Dit is de modale klasse. Een distributie kan twee of meer modi hebben, in welk geval deze wordt aangeroepen bimodaal Y multimodaal, respectievelijk.

U kunt de modus ook in gegroepeerde gegevens berekenen volgens de vergelijking:

Met:

-L.₁: ondergrens van de klasse waarin de modus wordt gevonden

-Δ₁: trek af tussen de frequentie van de modale klasse en de frequentie van de klasse die eraan voorafgaat.

-Δ_twee: aftrekken tussen de frequentie van de modale klasse en de frequentie van de volgende klasse.

-c: breedte van het interval dat de modus bevat

Harmonisch gemiddelde

Het harmonische gemiddelde wordt aangegeven met H. Als je een set hebt van n x waarden₁, X_twee, X₃..., het harmonische gemiddelde is het omgekeerde of omgekeerde van het rekenkundig gemiddelde van de inverse waarden.

Het is gemakkelijker om het door de formule te zien:

En als de gegroepeerde gegevens beschikbaar zijn, wordt de uitdrukking:

Waar:

-H: harmonisch gemiddelde

-F._ik: klasse frequentie

-m_ik: klassecijfer

-g: aantal klassen

-N = f₁ + F._twee + F.₃ +​

Geometrisch gemiddelde

Als ze hebben n positieve getallen x₁, X_twee, X₃..., Zijn geometrisch gemiddelde G wordt berekend door de n-de wortel van het product van alle getallen:

In het geval van gegroepeerde gegevens kan worden aangetoond dat de decimale logaritme van de geometrisch gemiddelde log G wordt gegeven door:

Waar:

-G: geometrisch gemiddelde

-F._ik: klasse frequentie

-m_ik: het klassenteken

-g: aantal klassen

-N = f₁ + F._twee + F.₃ +​

Verband tussen H, G en X

Het is altijd waar dat:

H ≤ G ≤ X

Meest gebruikte definities

De volgende definities zijn vereist om de waarden te vinden die in de bovenstaande formules worden beschreven:

Frequentie

Frequentie wordt gedefinieerd als het aantal keren dat een gegevensstuk wordt herhaald.

Rang

Het is het verschil tussen de hoogste en laagste waarden, aanwezig in de verdeling.

Aantal lessen

Om te weten in hoeveel klassen we de gegevens groeperen, gebruiken we enkele criteria, bijvoorbeeld de volgende:

Grenzen

De extreme waarden van elke klasse of interval worden aangeroepen limieten en elke klasse kan zowel goed gedefinieerde limieten hebben, in welk geval het een lagere en een hogere limiet heeft. Of het kan open limieten hebben, wanneer een bereik wordt gegeven, bijvoorbeeld waarden groter of kleiner dan een bepaald getal.

Klasse merk

Het bestaat simpelweg uit het middelpunt van het interval en wordt berekend door de bovengrens en de ondergrens te middelen.

Gap breedte

De gegevens kunnen worden gegroepeerd in klassen van gelijke of verschillende grootte, dit is de breedte of breedte. De eerste optie wordt het meest gebruikt, omdat het berekeningen veel gemakkelijker maakt, hoewel het in sommige gevallen noodzakelijk is dat de klassen verschillende breedtes hebben.

De breedte c Het interval kan worden bepaald door de volgende formule:

c = Bereik / N_c

Waar_c is het aantal klassen.

Oefening opgelost

Hieronder hebben we een reeks snelheidsmetingen in km / u, genomen met radar, die overeenkomen met 50 auto's die door een straat in een bepaalde stad reden:

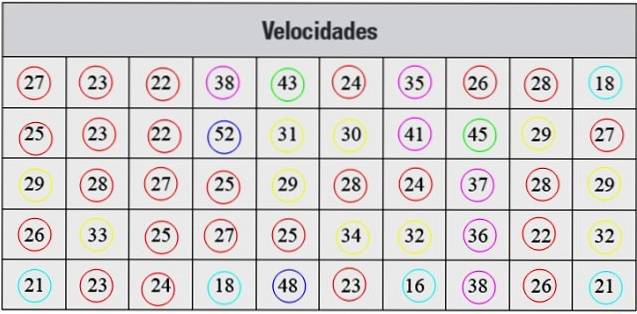
Oplossing

De gegevens die op deze manier worden gepresenteerd, zijn niet georganiseerd, dus de eerste stap is om deze in klassen te groeperen.

Stappen om de gegevens te groeperen en de tabel op te bouwen

Stap 1

Vind het bereik R:

R = (52 - 16) km / u = 36 km / u

Stap 2

Selecteer het aantal klassen N_c, volgens de gegeven criteria. Aangezien er 50 gegevens zijn, kunnen we N kiezen_c = 6.

Stap 3

Bereken de breedte c van het interval:

c = Bereik / N_c = 36/6 = 6

Stap 4

Vorm klassen en groepsgegevens als volgt: voor de eerste klasse wordt als ondergrens een waarde gekozen die iets kleiner is dan de laagste waarde in de tabel, daarna wordt de eerder berekende waarde van c = 6 bij deze waarde opgeteld, dus behaalt de bovengrens van de eerste klasse.

We gaan op dezelfde manier te werk om de rest van de klassen te bouwen, zoals weergegeven in de volgende tabel:

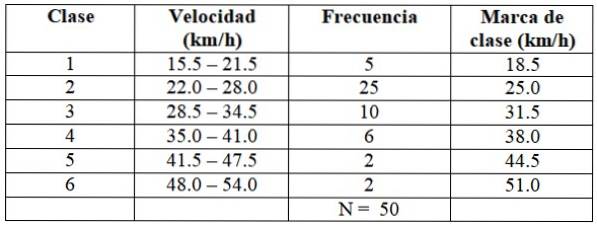
Elke frequentie correspondeert met een kleur in figuur 2, op deze manier wordt er voor gezorgd dat er geen waarde ontsnapt aan de telling..

Berekening van het gemiddelde

X = (5 x 18,5 +25 x 25,0 + 10 x 31,5 + 6 x 38,0 + 2 x 44,5 + 2 x 51,0) ÷ 50 = 29,03 km / u

Berekening van de mediaan

De mediaan is in klasse 2 van de tabel, aangezien er de eerste 30 gegevens van de verdeling zijn.

-Breedte van het interval waartoe de mediaan behoort: c = 6

-Ondergrens van het interval waarbij de mediaan is: B_M. = 22,0 km / u

-Aantal waarnemingen dat het interval f bevat_m = 25

-Totale gegevens gedeeld door 2: 50/2 = 25

-Aantal waarnemingen zijn er voordat van het interval met de mediaan: f_BM = 5

En de operatie is:

Mediaan = 22,0 + [(25-5) ÷ 25] x 6 = 26,80 km / u

Mode berekening

Mode zit ook in klasse 2:

-Intervalbreedte: c = 6

-Ondergrens van de klasse waarin de modus wordt gevonden: L₁ = 22,0

-Trek af tussen de frequentie van de modale klasse en de frequentie van de klasse die eraan voorafgaat: Δ₁ = 25-5 = 20

-Trek af tussen de frequentie van de modale klasse en de frequentie van de volgende klasse: Δ_twee = 25 - 10 = 15

Met deze gegevens is de operatie:

Modus = 22,0 + [20 ÷ (20 + 15)] x6 = 25,4 km / u

Berekening van het meetkundig gemiddelde

N = f₁ + F._twee + F.₃ +… = 50

logboek G = (5 x logboek 18,5 + 25 x logboek 25 + 10 x logboek 31,5 + 6 x logboek 38 + 2 × logboek 44,5 + 2 x logboek 51) / 50 =

log G = 1.44916053

G = 28,13 km / uur

Harmonische gemiddelde berekening

1 / H = (1/50) x [(5 / 18,5) + (25/25) + (10 / 31,5) + (6/38) + (2 / 44,5) + (2/51)] = 0,0366

H = 27,32 km / uur

Samenvatting van maatregelen van centrale tendens

De eenheden van de variabelen zijn km / u:

-Gemiddeld: 29.03

-Mediaan: 26,80

-Mode: 25.40

-Geometrisch gemiddelde: 28,13

-Harmonisch gemiddelde: 27.32

Referenties

1. Berenson, M. 1985. Statistieken voor management en economie. Interamericana S.A.
2. Canavos, G. 1988. Waarschijnlijkheid en statistiek: toepassingen en methoden. Mcgraw heuvel.
3. Devore, J. 2012. Waarschijnlijkheid en statistiek voor techniek en wetenschap. 8e. Editie. Cengage.
4. Levin, R. 1988. Statistieken voor beheerders. 2e. Editie. Prentice hal.
5. Spiegel, M. 2009. Statistieken. Schaum-serie. 4e Editie. Mcgraw heuvel.
6. Behandeling van gegroepeerde gegevens. Hersteld van: itchihuahua.edu.mx.
7. Walpole, R. 2007. Waarschijnlijkheid en statistiek voor techniek en wetenschappen. Pearson.