Atoommodel van Heisenberg

Wat is het atomaire model van Heisenberg?

De Atoommodel van Heisenberg (1927) introduceert het onzekerheidsprincipe in de elektronenorbitalen rond de atoomkern. De prominente Duitse natuurkundige legde de basis van de kwantummechanica om het gedrag van de subatomaire deeltjes waaruit een atoom bestaat te schatten..

Het onzekerheidsprincipe van Werner Heisenberg geeft aan dat het niet mogelijk is om de positie en het lineaire momentum van een elektron tegelijkertijd te kennen. Hetzelfde principe is van toepassing op de variabelen tijd en energie; dat wil zeggen, als we een idee hebben over de positie van het elektron, zullen we het lineaire momentum van het elektron niet kennen, en vice versa.

Kortom, het is niet mogelijk om de waarde van beide variabelen tegelijkertijd te voorspellen. Het voorgaande impliceert niet dat een van de bovengenoemde hoeveelheden niet precies bekend kan zijn. Zolang het apart is, is er geen belemmering om de rentewaarde te verkrijgen.

Er treedt echter onzekerheid op als het gaat om het gelijktijdig kennen van twee geconjugeerde grootheden, zoals positie en lineair momentum, en tijd samen met energie..

Dit principe komt voort uit een strikt theoretische redenering, als de enige haalbare verklaring om reden te geven voor wetenschappelijke observaties.

Kenmerken van het atomaire model van Heisenberg

In maart 1927 publiceerde Heisenberg zijn werk Over de perceptuele inhoud van kinematica en kwantumtheoretische mechanica, waar u het onzekerheids- of onbepaaldheidsprincipe hebt beschreven.

Dit principe, fundamenteel in het atomaire model voorgesteld door Heisenberg, wordt gekenmerkt door het volgende:

• Het onzekerheidsprincipe komt naar voren als een verklaring die complementair is aan de nieuwe atoomtheorieën over het gedrag van elektronen. Ondanks het gebruik van meetinstrumenten met hoge precisie en gevoeligheid, is de onbepaaldheid nog steeds aanwezig in elke experimentele test.
• Vanwege het onzekerheidsprincipe zal bij het analyseren van twee gerelateerde variabelen, als je een nauwkeurige kennis hebt van een van deze variabelen, de onzekerheid over de waarde van de andere variabele steeds groter worden..
• Het momentum en de positie van een elektron of ander subatomair deeltje kunnen niet tegelijkertijd worden gemeten.
• De relatie tussen beide variabelen wordt gegeven door een ongelijkheid. Volgens Heisenberg is het product van de variaties van het lineaire momentum en de positie van het deeltje altijd groter dan het quotiënt tussen de plankconstante (6,62606957 (29) × 10 ^{-3. 4} Jules x seconden) en 4π, zoals beschreven in de volgende wiskundige uitdrukking:

De legenda die overeenkomt met deze uitdrukking is de volgende:

∆p: onbepaaldheid van het lineaire moment.

∆x: onbepaaldheid van positie.

h: Plank's constante.

π: nummer pi 3.14.

• Gezien het bovenstaande heeft het product van de onzekerheden als ondergrens de verhouding h / 4π, wat een constante waarde is. Daarom, als een van de grootheden naar nul neigt, moet de andere in dezelfde verhouding toenemen.
• Deze relatie is geldig voor alle paren geconjugeerde canonieke grootheden. Bijvoorbeeld: het onzekerheidsprincipe van Heisenberg is perfect toepasbaar op het energie-tijdpaar, zoals hieronder beschreven:

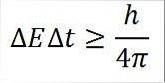
In deze uitdrukking:

∆E: onbepaaldheid van energie.

∆t: onbepaaldheid van tijd.

h: Plank's constante.

π: nummer pi 3.14.

• Uit dit model volgt dat absoluut causaal determinisme in geconjugeerde canonieke variabelen onmogelijk is, aangezien men om deze relatie vast te stellen kennis moet hebben van de beginwaarden van de studievariabelen..
• Bijgevolg is het Heisenberg-model gebaseerd op probabilistische formuleringen, vanwege de willekeur tussen de variabelen op subatomaire niveaus..

Experimentele tests

Het Heisenberg-onzekerheidsprincipe komt naar voren als de enige mogelijke verklaring voor de experimentele tests die plaatsvonden tijdens de eerste drie decennia van de 21e eeuw..

Voordat Heisenberg het onzekerheidsprincipe verkondigde, suggereerden de toen geldende voorschriften dat de variabelen lineair momentum, positie, impulsmoment, tijd, energie, onder andere, voor subatomaire deeltjes operationeel werden gedefinieerd..

Dit betekende dat ze werden behandeld alsof ze klassieke natuurkunde waren; dat wil zeggen, een beginwaarde werd gemeten en de eindwaarde werd geschat volgens de vooraf vastgestelde procedure.

Dit impliceerde het definiëren van een referentiesysteem voor metingen, het meetinstrument en de manier van gebruik van dat instrument, in overeenstemming met de wetenschappelijke methode..

Dienovereenkomstig moesten de variabelen beschreven door subatomaire deeltjes zich op een deterministische manier gedragen. Dat wil zeggen, zijn gedrag moest nauwkeurig en precies worden voorspeld..

Elke keer dat een dergelijke test werd uitgevoerd, was het echter onmogelijk om de theoretisch geschatte waarde in de meting te verkrijgen.. 

De metingen waren vertekend door de natuurlijke omstandigheden van het experiment, en het verkregen resultaat was niet bruikbaar om de atoomtheorie te verrijken.

Voorbeeld

Bijvoorbeeld: als het een kwestie is van het meten van de snelheid en positie van een elektron, dan moet bij de opzet van het experiment rekening worden gehouden met de botsing van een foton van licht met het elektron..

Deze botsing veroorzaakt een variatie in de snelheid en de intrinsieke positie van het elektron, waarmee het object van de meting wordt gewijzigd door de experimentele omstandigheden..

Daarom moedigt de onderzoeker het optreden van een onvermijdelijke experimentele fout aan, ondanks de nauwkeurigheid en precisie van de gebruikte instrumenten..

Kwantummechanica anders dan klassieke mechanica

Naast het bovenstaande stelt het onbepaaldheidsprincipe van Heisenberg dat de kwantummechanica per definitie anders werkt dan de klassieke mechanica..

Daarom wordt aangenomen dat nauwkeurige kennis van metingen op subatomair niveau wordt beperkt door de dunne lijn die de klassieke en kwantummechanica scheidt..

Beperkingen van het Heisenberg-model

Ondanks de verklaring van de onbepaaldheid van subatomaire deeltjes en het vaststellen van de verschillen tussen klassieke en kwantummechanica, stelt het atomaire model van Heisenberg geen enkele vergelijking vast om de willekeur van dit soort verschijnselen te verklaren..

Bovendien impliceert het feit dat de relatie tot stand komt door een ongelijkheid dat het scala aan mogelijkheden voor het product van twee geconjugeerde canonieke variabelen onbepaald is. Bijgevolg is de onzekerheid die inherent is aan subatomaire processen aanzienlijk..

Artikelen van belang

Het atomaire model van Schrödinger.

Atomic de Broglie-model.

Chadwick Atomic Model.

Perrin's atomaire model.

Thomson's atomaire model.

Atoommodel van Dalton.

Atoommodel van Dirac Jordan.

Atoommodel van Democritus.

Atoommodel van Leucippus.

Bohr atomair model.

Atoommodel van Sommerfeld.

Huidig ​​atomair model.

Referenties

1. Beyler, R. (1998). Werner Heisenberg. Encyclopædia Britannica, Inc. Hersteld van: britannica.com
2. Het Heisenberg-onzekerheidsprincipe (s.f.). Hersteld van: hiru.eus
3. García, J. (2012). Heisenbergs onzekerheidsprincipe. Hersteld van: hiberus.com
4. Atoommodellen (s.f.). Nationale Autonome Universiteit van Mexico. Mexico DF, Mexico. Hersteld van: asesorias.cuautitlan2.unam.mx
5. Werner Heisenberg (s.f.). Hersteld van: the-history-of-the-atom.wikispaces.com
6. Wikipedia, The Free Encyclopedia (2018). Plank is constant. Hersteld van: es.wikipedia.org
7. Wikipedia, The Free Encyclopedia (2018). Heisenbergs onbepaaldheidsrelatie. Hersteld van: es.wikipedia.org