De Het atomaire model van Schrödinger werd ontwikkeld door Erwin Schrödinger in 1926. Dit voorstel staat bekend als het kwantummechanische model van het atoom, en beschrijft het golfgedrag van het elektron.
Schrödinger suggereerde dat de beweging van de elektronen in het atoom overeenkwam met de dualiteit van golf en deeltje, en dat de elektronen bijgevolg als staande golven rond de kern konden bewegen..
Schrödinger, die in 1933 de Nobelprijs ontving voor zijn bijdragen aan de atoomtheorie, ontwikkelde de gelijknamige vergelijking om de waarschijnlijkheid te berekenen dat een elektron zich in een specifieke positie bevindt..
Artikel index
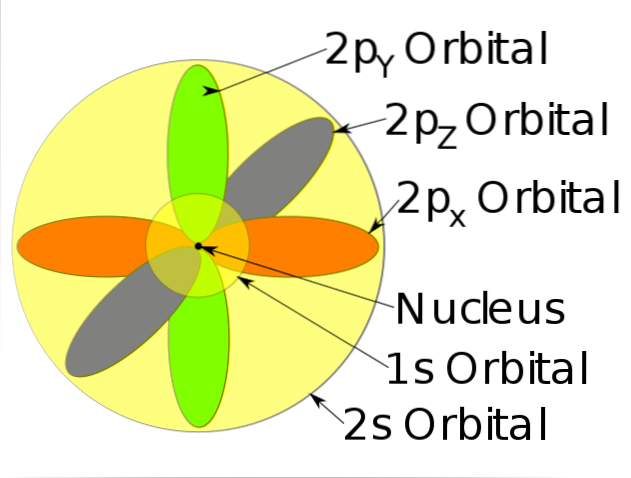
-Beschrijf de beweging van elektronen als staande golven.
-Elektronen bewegen constant, dat wil zeggen, ze hebben geen vaste of gedefinieerde positie binnen het atoom.
-Dit model voorspelt niet de locatie van het elektron, noch beschrijft het het pad dat het binnen het atoom aflegt. Stel gewoon een waarschijnlijkheidszone in om het elektron te lokaliseren.
-Deze kansgebieden worden atomaire orbitalen genoemd. De orbitalen beschrijven een translatiebeweging rond de kern van het atoom.
-Deze atomaire orbitalen hebben verschillende energieniveaus en subniveaus en kunnen worden gedefinieerd tussen elektronenwolken.
-Het model beschouwt de stabiliteit van de kern niet, het verwijst alleen naar het verklaren van de kwantummechanica die geassocieerd is met de beweging van elektronen in het atoom..
Het atomaire model van Schrödinger is gebaseerd op de Broglie-hypothese, evenals op de eerdere atomaire modellen van Bohr en Sommerfeld.
Broglie stelde voor dat net zoals golven eigenschappen hebben van deeltjes, deeltjes eigenschappen hebben van golven, met een bijbehorende golflengte. Iets dat destijds veel verwachting wekte, aangezien Albert Einstein zelf zijn theorie onderschrijft.
De Broglie-theorie had echter een tekortkoming, namelijk dat de betekenis van het idee zelf niet goed werd begrepen: een elektron kan een golf zijn, maar waarvan? Het is dan dat de figuur van Schrödinger een antwoord lijkt te geven.
Om dit te doen, vertrouwde de Oostenrijkse natuurkundige op Young's experiment, en op basis van zijn eigen waarnemingen ontwikkelde hij de wiskundige uitdrukking die zijn naam draagt.
Hier zijn de wetenschappelijke grondslagen van dit atomaire model:
De de Broglie-hypothese over de golvende en corpusculaire aard van materie kan worden aangetoond met behulp van Young's experiment, ook wel bekend als het dubbel-spleet-experiment..
De Engelse wetenschapper Thomas Young legde de basis voor het atomaire model van Schrödinger toen hij in 1801 het experiment uitvoerde om de golfkarakteristiek van licht te verifiëren..
Tijdens zijn experimenten verdeelde Young de emissie van een lichtstraal die door een klein gaatje door een observatiekamer ging. Deze verdeling wordt bereikt door een kaart van 0,2 millimeter te gebruiken, parallel aan de balk..
Het ontwerp van het experiment was zo gemaakt dat de lichtstraal breder was dan de kaart, dus bij het horizontaal plaatsen van de kaart werd de straal verdeeld in twee ongeveer gelijke delen. De output van de lichtstralen werd gestuurd door een spiegel.
Beide lichtstralen raakten een muur in een donkere kamer. Daar werd het interferentiepatroon tussen de twee golven aangetoond, wat aantoonde dat licht zich zowel als een deeltje als als een golf kon gedragen..
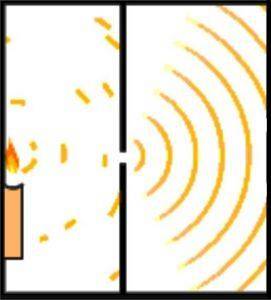
Een eeuw later versterkte Albert Einsten het idee met behulp van de principes van de kwantummechanica..
Schrödinger ontwikkelde twee wiskundige modellen, waarbij onderscheid werd gemaakt tussen wat er gebeurt, afhankelijk van of de kwantumtoestand met de tijd verandert of niet.
Voor atomaire analyse publiceerde Schrödinger eind 1926 de tijdonafhankelijke Schrödingervergelijking, die is gebaseerd op het feit dat golffuncties zich gedragen als staande golven..
Dit houdt in dat de golf niet beweegt, de knooppunten, dat wil zeggen de evenwichtspunten, dienen als een draaipunt voor de rest van de structuur om eromheen te bewegen en beschrijft een specifieke frequentie en amplitude..
Schrödinger definieerde de golven die elektronen beschrijven als stationaire of orbitale toestanden, en ze worden op hun beurt geassocieerd met verschillende energieniveaus.
De tijdonafhankelijke Schrödingervergelijking is als volgt:
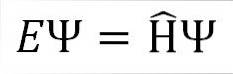
Waar:
EN: constante van evenredigheid.
Ψ: golffunctie van het kwantumsysteem.
Η ̂: Hamiltoniaanse operator.
De tijdonafhankelijke Schrödingervergelijking wordt gebruikt wanneer het waarneembare dat de totale energie van het systeem vertegenwoordigt, bekend als de Hamiltoniaanse operator, niet afhankelijk is van de tijd. De functie die de totale golfbeweging beschrijft, is echter altijd afhankelijk van de tijd..
De Schrödingervergelijking geeft aan dat als we een golffunctie Ψ hebben, en de Hamiltoniaanse operator daarop werkt, de evenredigheidsconstante E de totale energie van het kwantumsysteem in een van zijn stationaire toestanden vertegenwoordigt..
Toegepast op het atomaire model van Schrödinger, als het elektron in een gedefinieerde ruimte beweegt, zijn er discrete energiewaarden, en als het elektron vrij in de ruimte beweegt, zijn er continue energie-intervallen.
Vanuit wiskundig oogpunt zijn er verschillende oplossingen voor de Schrödingervergelijking, elke oplossing impliceert een andere waarde voor de evenredigheidsconstante E.
Volgens het onzekerheidsprincipe van Heisenberg is het niet mogelijk om de positie en energie van een elektron in te schatten. Daarom erkennen wetenschappers dat de schatting van de locatie van het elektron in het atoom onnauwkeurig is..
De postulaten van het atomaire model van Schrödinger zijn als volgt:
-Elektronen gedragen zich als staande golven die in de ruimte worden verdeeld volgens de golffunctie.
-Elektronen bewegen zich in orbitalen in het atoom. Dit zijn gebieden waar de kans om een elektron te vinden aanzienlijk hoger is. De genoemde kans is evenredig met het kwadraat van de golffunctie Ψtwee.
De elektronenconfiguratie van het atomaire model van Schrödinguer verklaart de periodieke eigenschappen van atomen en de bindingen die ze vormen.
Het atomaire model van Schrödinger houdt echter geen rekening met de spin van elektronen, en evenmin met variaties in het gedrag van snelle elektronen als gevolg van relativistische effecten..
Atomic de Broglie-model.
Chadwick Atomic Model.
Atoommodel van Heisenberg.
Perrin's atomaire model.
Thomson's atomaire model.
Atoommodel van Dalton.
Atoommodel van Dirac Jordan.
Atoommodel van Democritus.
Atoommodel van Leucippus.
Bohr atomair model.
Atoommodel van Sommerfeld.
Huidig atomair model.
Niemand heeft nog op dit artikel gereageerd.