
Kwantummechanisch model van het atoomgedrag, voorbeelden
De kwantummechanisch model van het atoom veronderstelt dat deze wordt gevormd door een centrale kern die bestaat uit protonen en neutronen. Negatief geladen elektronen omringen de kern in diffuse gebieden die bekend staan als orbitalen..
De vorm en omvang van elektronische orbitalen wordt bepaald door verschillende grootheden: het potentieel van de kern en de gekwantiseerde niveaus van energie en impulsmoment van de elektronen.
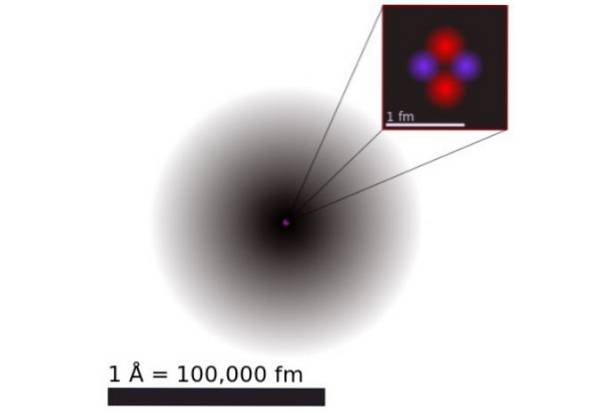
Volgens de kwantummechanica hebben elektronen een dubbel golfdeeltjesgedrag en zijn ze op atomaire schaal diffuus en puntloos. De afmetingen van het atoom worden praktisch bepaald door de uitbreiding van de elektronische orbitalen die de positieve kern omringen.
Figuur 1 toont de structuur van het heliumatoom, dat een kern heeft met twee protonen en twee neutronen. Deze kern is omgeven door de waarschijnlijkheidswolk van de twee elektronen die de kern omringen, die honderdduizend keer kleiner is. In de volgende afbeelding zie je het heliumatoom, met de protonen en neutronen in de kern en de elektronen in orbitalen.

De grootte van een heliumatoom is in de orde van één Angstrom (1 Å), dat is 1 x 10 ^ -10 m. Terwijl de grootte van de kern in de orde van a is femtometer (1 fm), dat is 1 x 10 ^ -15 m.
Ondanks dat het zo relatief klein is, is 99,9% van het atoomgewicht geconcentreerd in de kleine kern. Dit komt doordat de protonen en neutronen 2000 keer zwaarder zijn dan de elektronen die hen omringen..
Artikel index
- 1 Atoomschaal en kwantumgedrag
- 1.1 Eerste kwantummodellen
- 2 Dynamiek van materiële golven
- 2.1 Atomaire orbitalen
- 2.2 Quantum-nummers
- 3 Vorm en grootte van orbitalen
- 3.1 De draai
- 4 referenties
Atoomschaal en kwantumgedrag
Een van de concepten die de meeste invloed hadden op de ontwikkeling van het atomaire model, was dat van dualiteit golf - deeltje: de ontdekking dat bij elk materieel object een materiegolf hoort.
De formule voor het berekenen van de golflengte λ geassocieerd met een materieel object werd voorgesteld door Louis De Broglie in 1924 en is het volgende:
λ = u / (m v)
Waar h is de constante van Planck, m het deeg en v snelheid.
Volgens het principe van De Broglie heeft elk object een tweeledig gedrag, maar afhankelijk van de schaal van de interacties, de snelheid en de massa, kan het golfgedrag meer op de voorgrond treden dan het deeltjesgedrag of omgekeerd..
Het elektron is licht, de massa is 9,1 × 10 ^ -31 kg. De typische snelheid van een elektron is 6000 km / s (vijftig keer langzamer dan de lichtsnelheid). Deze snelheid komt overeen met energiewaarden in het bereik van tientallen elektronvolt..
Met de bovenstaande gegevens, en door de formule van de Broglie te gebruiken, kan de golflengte voor het elektron worden verkregen:
λ = 6,6 x 10 ^ -34 J s / (9,1 × 10 ^ -31 kg 6 x 10 ^ 6 m / s) = 1 x 10 ^ -10 m = 1 Å
Het elektron heeft op de typische energieën van atomaire niveaus een golflengte van dezelfde orde van grootte als die van de atomaire schaal, zodat het op die schaal een golfgedrag heeft en geen deeltje..
Eerste kwantummodellen
Met het idee in gedachten dat het elektron op atomaire schaal golfgedrag vertoont, werden de eerste atomaire modellen op basis van kwantumprincipes ontwikkeld. Onder deze valt het Bohr-atoommodel op, dat perfect het emissiespectrum van waterstof voorspelde, maar niet dat van andere atomen.
Het Bohr-model, en later het Sommerfeld-model, waren semi-klassieke modellen. Dat wil zeggen, het elektron werd behandeld als een deeltje dat werd onderworpen aan de elektrostatische aantrekkingskracht van de kern die eromheen cirkelde, gereguleerd door de tweede wet van Newton..
Naast klassieke banen hielden deze eerste modellen er rekening mee dat het elektron een bijbehorende materiaalgolf had. Alleen banen waarvan de omtrek een geheel aantal golflengten was, waren toegestaan, aangezien degenen die niet aan dit criterium voldoen, verdwijnen door destructieve interferentie..
Op dat moment verschijnt de kwantisering van energie voor het eerst in de atomaire structuur..
Het woord quantum Het komt precies door het feit dat het elektron slechts enkele discrete energiewaarden binnen het atoom kan aannemen. Dit valt samen met de bevinding van Planck, die bestond in de ontdekking dat een straling een frequentie heeft F. interageert met materie in pakketjes energie E = h f, waar h is de constante van Planck.
Dynamiek van materiële golven
Er bestond geen twijfel meer over dat het elektron zich op atomair niveau gedroeg als een materiële golf. De volgende stap was om de vergelijking te vinden die hun gedrag bepaalt. Die vergelijking is niet meer of minder dan de Schrodinger-vergelijking, voorgesteld in 1925.
Deze vergelijking heeft betrekking op en bepaalt de golffunctie ψ geassocieerd met een deeltje, zoals het elektron, met zijn interactiepotentiaal en zijn totale energie EN. De wiskundige uitdrukking is:


Gelijkheid in de Schrodinger-vergelijking geldt alleen voor enkele waarden van de totale energie EN, die aanleiding geven tot de kwantisering van energie. De golffunctie van de elektronen onderworpen aan het potentieel van de kern wordt verkregen uit de oplossing van de Schrodinger-vergelijking.
Atomaire orbitalen
De absolute waarde van de golffunctie in het kwadraat |ψ| ^ 2, geeft de waarschijnlijkheidsamplitude van het vinden van het elektron op een bepaalde positie.
Dit leidt tot het concept van orbitaal, dat wordt gedefinieerd als het diffuse gebied dat wordt ingenomen door het elektron met een waarschijnlijkheidsamplitude die niet gelijk is aan nul, voor de discrete waarden van energie en impulsmoment bepaald door de oplossingen van de Schrodinger-vergelijking.
De kennis van de orbitalen is erg belangrijk, omdat het de atomaire structuur, de chemische reactiviteit en de mogelijke bindingen om moleculen te vormen beschrijft.
Het waterstofatoom is het eenvoudigste van allemaal, omdat het een eenzaam elektron heeft en het is het enige dat een exacte analytische oplossing van de Schrodinger-vergelijking toelaat.
Dit eenvoudige atoom heeft een kern die bestaat uit een proton, dat een centraal potentieel van Coulomb-aantrekking produceert dat alleen afhangt van de straal. r, het is dus een systeem met sferische symmetrie.
De golffunctie hangt af van de positie, gegeven door de sferische coördinaten ten opzichte van de kern, aangezien het elektrische potentieel centrale symmetrie heeft.
Bovendien kan de golffunctie worden geschreven als het product van een functie die alleen afhangt van de radiale coördinaat, en een andere die afhangt van de hoekcoördinaten:

Kwantumgetallen
De oplossing van de radiale vergelijking levert de discrete energiewaarden op, die afhangen van een geheel getal n, genaamd de Hoofdkwantumnummer, die positieve gehele getallen 1, 2, 3, ... kan aannemen
Discrete energiewaarden zijn negatieve waarden die worden gegeven door de volgende formule:

De oplossing van de hoekvergelijking definieert de gekwantiseerde waarden van het impulsmoment en zijn z-component, waardoor de kwantumgetallen ontstaan l Y ml.
Het kwantumgetal van impulsmoment l gaat van 0 tot n-1. Kwantumnummer ml heet het magnetische kwantumgetal en gaat van -l tot +l. Ja, bijvoorbeeld l waar 2 het magnetische kwantumgetal de waarden -2, -1, 0, 1, 2 zou aannemen.
Vorm en grootte van de orbitalen
Het radiale bereik van de orbitaal wordt bepaald door de radiogolffunctienaar de. Het is groter naarmate de energie van het elektron toeneemt, dat wil zeggen naarmate het belangrijkste kwantumgetal toeneemt.
De radiale afstand wordt meestal gemeten in Bohr-stralen, die voor de laagste energie van waterstof 5,3 x 10-11 m = 0,53 Å is.

Maar de vorm van de orbitalen wordt bepaald door de waarde van het kwantumgetal van het impulsmoment. Als l = 0 hebben we een sferische orbitaal genaamd s, als l = 1 hebben we een gelobde orbitaal genaamd p, die drie oriëntaties kan hebben volgens het magnetische kwantumgetal. De volgende afbeelding toont de vorm van de orbitalen.
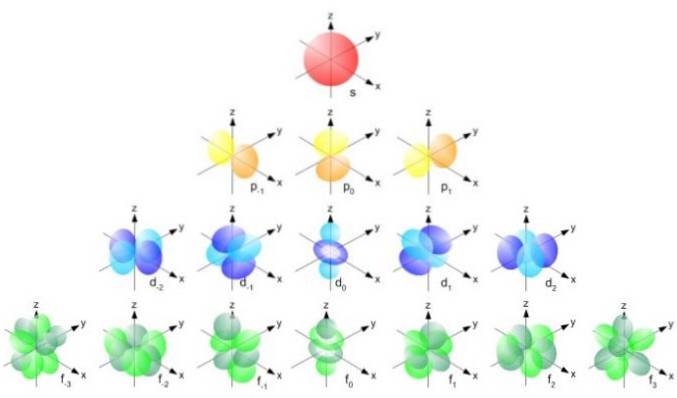
Deze orbitalen pakken zich in elkaar op volgens de energie van de elektronen. De volgende afbeelding toont bijvoorbeeld de orbitalen in een natriumatoom.
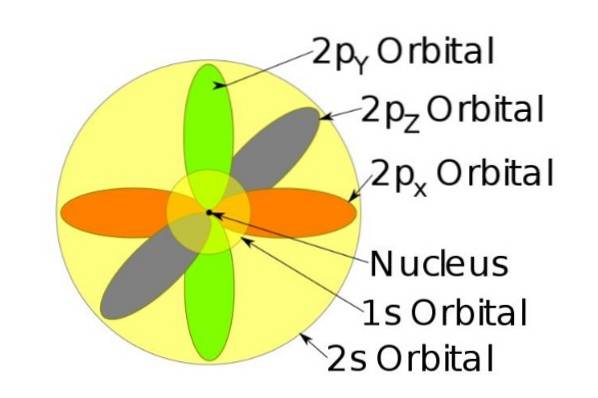
De draai
Het kwantummechanische model van de Schrödingervergelijking houdt geen rekening met de spin van het elektron. Maar er wordt rekening mee gehouden door het Pauli-uitsluitingsprincipe, dat aangeeft dat orbitalen kunnen worden gevuld met maximaal twee elektronen met spinkwantumgetallen s = + ½ en s = -½.
Het natriumion heeft bijvoorbeeld 10 elektronen, dat wil zeggen, als we naar de vorige afbeelding verwijzen, zijn er twee elektronen voor elke orbitaal.
Maar als het het neutrale natriumatoom is, zijn er 11 elektronen, waarvan de laatste een 3s-orbitaal zouden innemen (niet weergegeven in de figuur en met een grotere straal dan de 2s). De spin van het atoom is bepalend voor de magnetische eigenschappen van een stof.
Referenties
- Alonso - Finn. Kwantum- en statistische grondslagen. Addison Wesley.
- Eisberg - Resnick. Kwantumfysica. Limusa - Wiley.
- Gasiorowicz. Kwantumfysica. John Wiley & Sons.
- HSC. Natuurkundecursus 2. Jacaranda plus.
- Wikipedia. Schrodinger's atomaire model. Hersteld van: Wikipedia.com


Niemand heeft nog op dit artikel gereageerd.