In elliptische beweging beschrijft de mobiel een ellips, net zoals de planeten rond de zon doen, en de maan en kunstmatige satellieten rond de aarde, om maar een paar bekende voorbeelden te noemen..
De kracht die tot deze beweging leidt, is de zwaartekracht, een centrale kracht. Dit soort krachten zijn gericht naar (of van) een vast punt O, en hun modulus hangt af van de afstand tot dat punt. Als r de afstand is en ofr is de eenheidsvector in radiale richting, de centrale kracht F. is een vectorfunctie van de vorm:
F. = F (r) ofr
Met wat wiskunde kan worden aangetoond dat de beweging van een object onder invloed van de zwaartekracht een van deze vier banen volgt: ellips, omtrek, hyperbool of parabool.
Enkele van de belangrijkste kenmerken van elliptische beweging onder centrale kracht zijn:
-Het impulsmoment ten opzichte van O wordt behouden, genoemd L. en dat wordt berekend via het vectorproduct tussen de positie- en snelheidsvectoren: L. r × mv, waarbij m de massa van het bewegende object voorstelt.
-De elliptische baan ligt in het vlak bepaald door de vectoren r Y v.
-Van het behoud van impulsmoment de zogenaamde wet van gebieden, waaruit blijkt dat de gsm in gelijke tijden gelijke gebieden aflegt.
-Mechanische energie wordt ook behouden bij elliptische beweging, als er geen dissipatieve krachten zijn.
-De tijd die het mobieltje nodig heeft om een baan en zijn totale energie te geven, hangt alleen af van de lengte "a" van de semi-hoofdas van de ellips..
Hoewel het object zowel in cirkelvormige als elliptische beweging beweegt in een gesloten en zich herhalend pad, dat wil zeggen periodiek, zijn er duidelijke verschillen tussen de ene beweging en de andere, zoals:
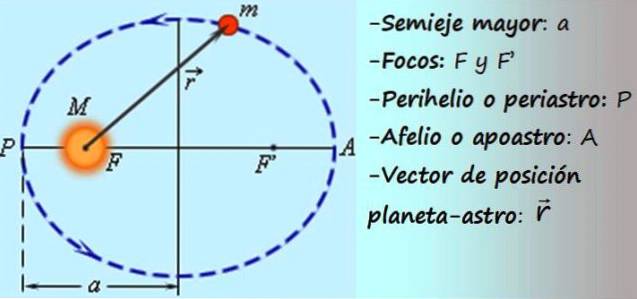
-In cirkelvormige beweging beschrijft de mobiel een omtrek waarvan de straal (afstand tot het midden van het pad) constant is, terwijl het bij elliptische beweging een ellips beschrijft, waarbij de afstand tot het midden van het pad variabel is (zie figuur 1).
-In het geval van een uniforme cirkelvormige beweging MCU veegt de mobiele telefoon gelijke hoeken in gelijke tijden, maar bij planetaire elliptische beweging worden gelijke gebieden in gelijke tijden geveegd. Dit is de wet van gebieden, ook wel bekend als Keplers tweede wet van planetaire beweging..
Bij elliptische beweging afgeleid van zwaartekracht, is de periode T van beweging de tijd die de planeet of satelliet (m) nodig heeft om een elliptische draai rond de zon of de aarde (M) te maken. Door het behoud van energie toe te passen, volgt hieruit dat het evenredig is met de kubus van de lengte van de halve hoofdas van de ellips:
Waar G de universele gravitatieconstante is: 6,67 x 10-elf N ∙ mtwee/ kgtwee, M is de massa van de zon, de aarde of het object dat de interactie op m veroorzaakt en 'a' is de lengte van de semi-hoofdas.
De totale energie voor het planeet (m) - Zon (M) -systeem is:
De grootte van het impulsmoment op een punt op de elliptische baan hangt ook af van de lengte van de semi-hoofdas, evenals van de excentriciteit "e", een dimensieloze parameter die aangeeft hoe afgeplat de ellips is. Als e = 0, wordt de ellips een cirkel.
De grootte van de snelheid wordt gegeven door de volgende vergelijking:
Waar r de afstand is tussen een punt op de baan (locatie van de planeet) en het brandpunt (zon).
De eerste wet van Kepler stelt dat de beweging van de planeten rond de zon een elliptisch pad volgt, met de zon in een van de brandpunten. Sommige kometen die periodiek de aarde bezoeken, zoals Halley's komeet, volgen ook een elliptische beweging..
Afgezien van deze elliptische translatiebeweging en die van rotatie om hun as, hebben de planeten hun eigen bewegingen vanwege de complexe gravitatie-interacties met de andere planeten en hemellichamen in het zonnestelsel. Op deze manier zijn de precessie- en nutatiebewegingen die de aarde bezit en die het gevolg zijn van de gezamenlijke aantrekkingskracht van de zon en de maan..
In precessie beschrijft de aardas een kegel terwijl deze roteert rond de as loodrecht op het plan of de ecliptica. En in nutatie, die bovenop precessie wordt gelegd, oscilleert de aardas elke 18,6 jaar op en neer in een elliptische lus. In totaal 1385 van deze lussen geleden in 25.767 jaar, de periode van de precessie van de aardas.
In oceaanwater voert een deeltje een elliptische beweging uit, waarbij de ellips steeds meer afgevlakt wordt naarmate de diepte toeneemt. Aan de andere kant, als het water diep is, is de beweging van de deeltjes cirkelvormig.
Wat er gebeurt, is dat wanneer de golf de kust nadert, wrijvingskrachten optreden dankzij de nabijheid van de bodem, en deze wrijving heeft de neiging om de beweging in het onderste deel van het traject te vertragen, terwijl de top zijn beweging voortzet..
Het resultaat is dat de omtrek vlakker wordt en het effect wordt geaccentueerd naarmate de diepte toeneemt..
Een fysieke slinger bestaat uit een stijve vaste stof die kan oscilleren in een vlak rond een as die er loodrecht op staat. Als het object vrij kan bewegen, kan het elke hoek rond de as beschrijven die het massamiddelpunt met het ophangpunt verbindt, en er ook omheen draaien..
Dankzij de rotatie van de aarde kan de slinger banen van ongeveer elliptische vorm beschrijven, die bekend staan als elliptische oscillatiemodus, gekenmerkt door een ander impulsmoment dan 0.
Er zijn ook de vlakke modus (impulsmoment 0) en de conische modus (ander impulsmoment dan 0), de laatste met een cirkelvormig pad op een horizontaal vlak.
De eerder beschreven elliptische bewegingen komen voor in de natuur, maar kunnen ook worden gebruikt om handige gadgets van te maken, zoals crosstrainers, die erg populair zijn bij het doen van aerobics..
Het zijn stationaire fietsen die in feite bestaan uit een stuur en twee pedalen die de persoon activeert door zichzelf met zijn gewicht te duwen, waarmee een ellips met zijn voeten wordt beschreven. Dit is een natuurlijke beweging met weinig impact die gunstig is omdat het veel spiergroepen door het lichaam beweegt..
Niemand heeft nog op dit artikel gereageerd.