Uniform versnelde rechtlijnige bewegingskarakteristieken, formules

De gelijkmatig versnelde rechtlijnige beweging Het is er een die langs een rechte lijn loopt en waarin de mobiel zijn snelheid met een constante snelheid verhoogt of verlaagt. Deze snelheid is de grootte die de snelheid beschrijft waarmee de snelheid verandert en wordt aangeroepen versnelling.

In het geval van uniform versnelde of gevarieerde rechtlijnige beweging (MRUV), is constante versnelling verantwoordelijk voor het veranderen van de grootte van de snelheid. Bij andere soorten beweging is versnelling ook in staat om de richting en het gevoel van snelheid te veranderen, of zelfs gewoon van richting te veranderen, zoals bij een uniforme cirkelvormige beweging..

Aangezien versnelling de verandering in snelheid in de loop van de tijd vertegenwoordigt, zijn de eenheden in het internationale systeem m / s^twee (meters over seconden in het kwadraat). Net als snelheid kan acceleratie een positief of negatief teken krijgen, afhankelijk van of de snelheid toeneemt of afneemt..

Een versnelling van zeg +3 m / s^twee betekent dat voor elke seconde die verstrijkt, de snelheid van de gsm met 3 m / s toeneemt. Als aan het begin van de beweging (op t = 0) de snelheid van de mobiel +1 m / s was, dan is deze na één seconde 4 m / s en na 2 seconden 7 m / s.

Bij gelijkmatig gevarieerde rechtlijnige bewegingen wordt rekening gehouden met de snelheidsvariaties die bewegende objecten dagelijks ervaren. Dit is een realistischer model dan de uniforme rechtlijnige beweging. Toch is het nog steeds vrij beperkt, omdat het de mobiele telefoon beperkt om alleen op een rechte lijn te reizen.

Artikel index

• 1 Kenmerken
  • 1.1 Afgelegde afstand van de v vs. grafiek t
• 2 Formules en vergelijkingen
• 3 Opgeloste oefeningen
  • 3.1 -Oefening opgelost 1
  • 3.2 - Opgeloste oefening 2
• 4 Toepassingen
• 5 referenties

Kenmerken

Dit zijn de belangrijkste kenmerken van gelijkmatig versnelde rechtlijnige beweging:

-Uurwerk loopt altijd rechtlijnig.

-De versnelling van de mobiele telefoon is constant, zowel in grootte als in richting en zin.

-De mobiele snelheid neemt lineair toe (of neemt af).

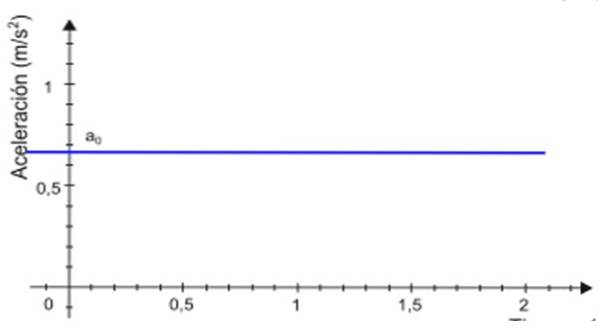
-Sinds de versnelling naar blijft constant in de tijd t, de grafiek van zijn grootte als functie van de tijd is een rechte lijn. In het voorbeeld in figuur 2 is de lijn blauw gekleurd en wordt de versnellingswaarde afgelezen op de verticale as, ongeveer +0,68 m / s^twee.

-De snelheidsgrafiek v over t het is een rechte lijn (in groen in figuur 3), waarvan de helling gelijk is aan de versnelling van de gsm. In het voorbeeld is de helling positief.

-De snede met de verticale as geeft de beginsnelheid aan, in dit geval is deze 0,4 m / s.

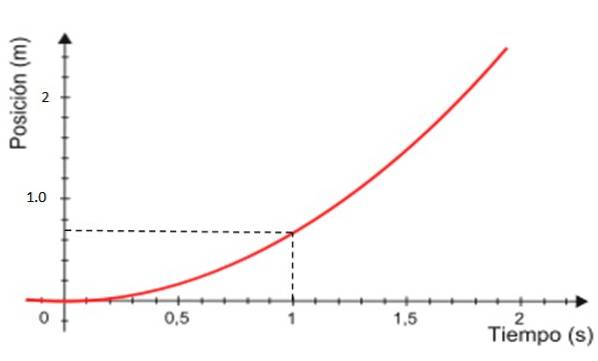
-Ten slotte is de grafiek van positie x versus tijd de curve die in rood is weergegeven in figuur 4, die altijd een parabool is.

Afgelegde afstand van de v vs. grafiek. t

Door de grafiek v vs. t, het berekenen van de afstand die door de gsm is afgelegd, is heel eenvoudig. De afgelegde afstand is gelijk aan het gebied onder de lijn dat binnen het gewenste tijdsinterval valt.

Stel dat u in het getoonde voorbeeld de afstand wilt weten die door de gsm is afgelegd tussen 0 en 1 seconde. Zie figuur 5 aan de hand van deze grafiek.

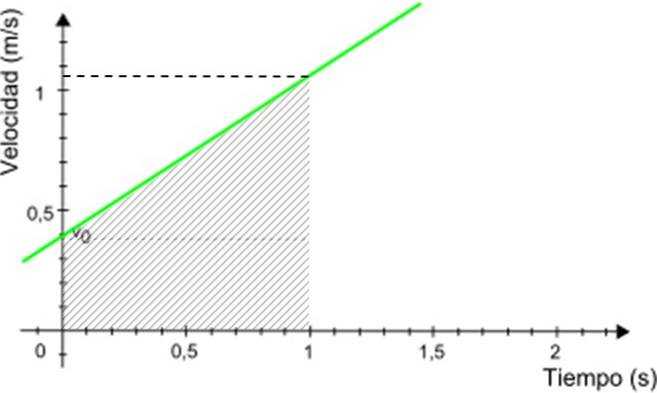
De gezochte afstand is numeriek equivalent aan de oppervlakte van de trapezium die in figuur 3 is gearceerd. De oppervlakte van de trapezium wordt gegeven door: (grote basis + kleine basis) x hoogte / 2

Afgelegde afstand = (0,4 + 1,05) x 1/2 m = 0,725 m

Het is ook mogelijk om het gearceerde gebied in een driehoek en een rechthoek te verdelen, de overeenkomstige gebieden te berekenen en ze bij elkaar op te tellen. De afgelegde afstand is positief, zelfs als het deeltje naar rechts of naar links gaat.

Formules en vergelijkingen

Zowel de gemiddelde versnelling als de momentane versnelling hebben dezelfde waarde in de MRUV, dus:

-Versnelling: naar = constant

Als de versnelling gelijk is aan 0, is de beweging gelijkmatig rechtlijnig, aangezien de snelheid in dit geval constant zou zijn. Het teken van naar Het kan positief of negatief zijn.

Omdat de versnelling de helling is van de lijn v versus t, is de vergelijking v (t):

-Snelheid als functie van de tijd: v (t) = v_of + Bij

Waar v_of is de waarde van de beginsnelheid van de mobiel

-Positie als functie van de tijd: x (t) = x_of + v_of t + ½at^twee 

Als je geen tijd hebt, maar in plaats daarvan snelheden en verplaatsingen, is er een zeer bruikbare vergelijking die wordt verkregen door de tijd van v (t) = v_of + Bij en het in de laatste vergelijking te vervangen. Gaat over:

-Vergelijking die geen tijd bevat: v^twee = v_of^twee +2.a.ΔX

Opgeloste oefeningen

Bij het oplossen van een kinematica-oefening is het belangrijk ervoor te zorgen dat de situatie is aangepast aan het te gebruiken model. De vergelijkingen van uniforme rechtlijnige beweging zijn bijvoorbeeld niet geldig voor versnelde beweging.

En die van de versnelde beweging gelden niet voor bijvoorbeeld een cirkelvormige of kromlijnige beweging. De eerste van deze oefeningen die hieronder wordt opgelost, combineert twee mobiele telefoons met verschillende bewegingen. Om het correct op te lossen, is het noodzakelijk om naar het juiste bewegingsmodel te gaan.

-Opgeloste oefening 1

Om de diepte van een put te achterhalen, laat een kind een munt vallen en activeert tegelijkertijd zijn timer, die stopt net nadat hij de munt het water heeft horen raken. De aflezing was 2,5 seconden. Wetende dat de geluidssnelheid in lucht 340 m / s is, berekent u de diepte van de put.

Oplossing

Worden h de diepte van de put. De munt legt deze afstand af in vrije val, een gelijkmatig gevarieerde verticale beweging, met beginsnelheid 0, als de munt valt, en een constante neerwaartse versnelling gelijk aan 9,8 m / s^twee. Neem een ​​moment t_m daarbij.

Zodra de munt het water raakt, gaat het geluid dat door de klik wordt veroorzaakt omhoog naar het oor van het kind, dat de stopwatch stopt wanneer hij het hoort. Er is geen reden om aan te nemen dat de geluidssnelheid verandert naarmate het de put omhoog komt, dus de beweging van het geluid is uniform rechtlijnig. Het geluid duurt even t_s om bij het kind te komen.

Bewegingsvergelijking voor de munt:

h = ½.g.t_m ^twee = 4,9 t_m ^twee

Waar ze zijn vervangen X Y naar van de vergelijking voor de positie gegeven in de vorige sectie, door h Y g.

Bewegingsvergelijking voor geluid:

h = v_s . t_s = 340 ton_s

Het gaat over de bekende vergelijking afstand = snelheid x tijd. Met deze twee vergelijkingen hebben we drie onbekenden: h, tm en ts. Voor de keren dat er een relatie is, is het bekend dat alles 2,5 seconden duurt om te gebeuren, daarom:

t_m + t_s = 2,5 s

Beide vergelijkingen gelijkstellen:

4,9 ton_m ^twee = 340 ton_s

Een van de tijden wissen en vervangen:

4,9 ton_m ^twee= 340. (2,5 - t_m​

Door de term rechts te ontwikkelen en termen om te zetten, verkrijgen we:

4,9 ton_m ^twee+340 t_m - 850 = 0

Dit is een kwadratische vergelijking met twee oplossingen: 2.416 en -71.8. De positieve oplossing wordt gekozen, wat logisch is, aangezien de tijd niet negatief kan zijn en in elk geval minder dan 2,5 seconden moet zijn. Voor deze tijd wordt het verkregen door de diepte van de put te vervangen door:

4,9 ton_m ^twee= 4,9 x 2,416^twee m = 28,6 m

-Oefening opgelost 2

Een auto met een snelheid van 90 km / u nadert een kruising met een stoplicht. Als het 70 m verder is, gaat het gele lampje branden, dit duurt 4 seconden. De afstand tussen het stoplicht en de volgende hoek is 50 m.

De chauffeur heeft deze twee opties: a) remmen met - 4 m / s^twee of b) versnellen tot + 2 m / s^twee. Met welke van de twee opties kan de bestuurder stoppen of de hele laan oversteken voordat het licht op rood wordt?

Oplossing

De startpositie van de coureur is x = 0 net als hij het gele lampje ziet branden. Het is belangrijk om de units op de juiste manier om te bouwen: 90 km / u is gelijk aan 25 m / s.

Volgens optie a) reist de bestuurder in de 4 seconden dat het gele lampje brandt:

x (t) = v_of t + ½at^twee= 25,4 -½. (- 4) .4^tweem = 68 m (Hij stopt 2 meter voor het stoplicht)

Bij het analyseren van optie b) hebben we:

x (t) = v_of t + ½at^twee= 25.t + ½.2.t^twee

Zolang het gele lampje brandt, reist de chauffeur als volgt:

x = 25,4 + ½,2,4^tweem = 116 m

Maar 116 m is minder dan de beschikbare afstand om bij de volgende hoek te komen, dat is 70 + 50 m = 120 m, daarom kan hij niet de hele straat oversteken voordat het rode licht gaat branden. De aanbevolen handeling is om te remmen en 2 meter van het verkeerslicht te blijven.

Toepassingen

Mensen ervaren de effecten van acceleratie dagelijks: bij het reizen met de auto of bus, die continu moeten remmen en optrekken om de snelheid aan te passen aan de obstakels op de weg. Versnelling wordt ook ervaren bij het omhoog of omlaag gaan in een lift.

Pretparken zijn plekken waar mensen betalen om de effecten van versnelling te ervaren en plezier te hebben.

In de natuur wordt een gelijkmatig gevarieerde rechtlijnige beweging waargenomen wanneer een object vrij valt, of wanneer het verticaal naar boven wordt gegooid en wacht tot het naar de grond terugkeert. Als de luchtweerstand wordt verwaarloosd, is de versnellingswaarde die van de zwaartekracht: 9,8 m / s2.

Referenties

1. Bauer, W. 2011. Physics for Engineering and Sciences. Deel 1. Mc Graw Hill, 40-45.
2. Figueroa, D. Physics Series for Sciences and Engineering. Deel 3e. Editie. Kinematica. 69-85.
3. Giancoli, D. Physics: principes met toepassingen. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Conceptuele fysische wetenschappen. 5^th. Ed Pearson. 14-18.
5. Kirkpatrick, L. 2007. Natuurkunde: een blik op de wereld. 6^ta Verkorte editie. Cengage leren. 15-19.
6. Wilson, J. 2011. Physics 10. Pearson Education. 116-119