
Trachtenberg-methode waaruit het bestaat, voorbeelden
De Trachtenberg-methode is een systeem om rekenkundige bewerkingen, voornamelijk vermenigvuldiging, op een gemakkelijke en snelle manier uit te voeren, zodra de regels bekend en beheerst zijn.
Het werd bedacht door de in Rusland geboren ingenieur Jakow Trachtenberg (1888-1953) toen hij een gevangene van de nazi's in een concentratiekamp was, als een vorm van afleiding om gezond verstand te behouden terwijl hij in gevangenschap doorging..
Artikel index
- 1 Waar het uit bestaat, voor- en nadelen
- 2 voorbeelden
- 2.1 - Vermenigvuldig een cijfer met 10 of met 11
- 2.2 - Vermenigvuldiging met getallen van 12 tot 19
- 2.3 - Uitbreiding van de regels voor vermenigvuldiging met 13,… tot 19
- 3 Regels voor producten van 6, 7 en 5
- 3.1 - Vermenigvuldiging met 6
- 3.2 - Vermenigvuldiging met 7
- 3.3 - Vermenigvuldiging met 5
- 4 Regels voor producten door 9
- 5 Vermenigvuldiging met 8, 4, 3 en 2
- 5.1 - Vermenigvuldiging met 8
- 5.2 - Vermenigvuldiging met 4
- 5.3 - Vermenigvuldiging met 3
- 5.4 - Vermenigvuldiging met 2
- 6 Vermenigvuldig met samengestelde cijfers
- 6.1 Oefening
- 7 referenties
Waar het uit bestaat, voor- en nadelen
Het voordeel van deze methode is dat om vermenigvuldiging uit te voeren, het niet nodig is om de tafels van vermenigvuldiging te onthouden, althans gedeeltelijk, het is alleen voldoende om te weten hoe te tellen en op te tellen, en om een cijfer door twee te delen.
Het nadeel is dat er geen universele regel is voor het vermenigvuldigen met een willekeurig getal, maar dat de regel varieert naargelang de vermenigvuldiger. De patronen zijn echter niet moeilijk te onthouden en maken het in principe mogelijk om bewerkingen uit te voeren zonder de hulp van papier en potlood..
In dit artikel zullen we ons concentreren op de regels voor snel vermenigvuldigen.
Voorbeelden
Om de methode toe te passen is het nodig om de regels te kennen, daarom gaan we ze een voor een en met voorbeelden presenteren:
- Vermenigvuldig een getal met 10 of met 11
Regel voor vermenigvuldiging met 10
-Om een getal met 10 te vermenigvuldigen, voegt u eenvoudig een nul toe aan de rechterkant. Bijvoorbeeld: 52 x 10 = 520.
Regels voor vermenigvuldigen met 11
-Aan het begin en einde van de figuur wordt een nul toegevoegd.
-Elk cijfer wordt toegevoegd met zijn buurman aan de rechterkant en het resultaat wordt onder het overeenkomstige cijfer van het oorspronkelijke cijfer geplaatst.
-Als het resultaat de negen overschrijdt, wordt de eenheid genoteerd en wordt er een punt op geplaatst om te onthouden dat we een eenheid hebben die wordt opgeteld bij de som van de volgende figuur met de buurman aan de rechterkant.
Gedetailleerd voorbeeld van vermenigvuldiging met 11
Vermenigvuldig 673179 met 11
06731790 x 11 =
--
= 7404969
De stappen die nodig zijn om tot dit resultaat te komen, geïllustreerd door kleuren, zijn als volgt:
-De 1 van de eenheid van de vermenigvuldiger (11) werd vermenigvuldigd met de 9 van de vermenigvuldiger (06731790) en 0 werd eraan toegevoegd. De eenheidscijfer van het resultaat werd verkregen: 9.
-Dan vermenigvuldigen we 1 met 7 en tellen we negen op bij 16 en we dragen 1, we plaatsen het tiencijfer: 6.
-Na het vermenigvuldigen van 1 met 1, geeft het optellen van de buurman aan de rechterkant 7 plus 1 die hij droeg als resultaat 9 voor de honderd.
-Het volgende cijfer wordt verkregen door 1 met 3 te vermenigvuldigen plus de buurman 1, dat is het 4 voor de duizenden cijfers.
-Vermenigvuldig 1 met 7 en tel de buurman 3 op, resulterend in 10, plaats de nul (0) als een tienduizend cijfer en duurt één.
-Dan 1 keer 6 plus buurman 7 resultaten 13 plus een 1 die resultaten 14 had, de 4 als honderdduizend cijfers en duurt 1.
-Ten slotte wordt 1 vermenigvuldigd met de nul die aan het begin werd toegevoegd, wat nul oplevert plus de buurman 6 plus een die werd gedragen. Het blijkt eindelijk 7 voor het cijfer dat overeenkomt met de miljoenen.
- Vermenigvuldiging met getallen van 12 tot 19
Om een getal met 12 te vermenigvuldigen:
-Een nul wordt aan het begin toegevoegd en nog een nul aan het einde van het te vermenigvuldigen cijfer.
-Elk cijfer van het te vermenigvuldigen cijfer wordt verdubbeld en opgeteld met zijn buurman aan de rechterkant.
-Als de som 10 overschrijdt, wordt een eenheid toegevoegd aan de volgende duplicatiebewerking en opgeteld bij de buurman.
Voorbeeld van vermenigvuldiging met 12
Vermenigvuldig 63247 met 12
0632470 x 12 =
-
758964
De details om tot dit resultaat te komen, strikt volgens de gestelde regels, worden weergegeven in de volgende afbeelding:

- Uitbreiding van de regels voor vermenigvuldiging met 13,… tot 19
De methode van vermenigvuldiging met 12 kan worden uitgebreid tot vermenigvuldiging met 13, 14 tot en met 19 door simpelweg de regel van verdubbeling te veranderen door verdrievoudiging voor het geval van dertien, verviervoudiging voor het geval van 14 enzovoort tot 19.
Regels voor producten van 6, 7 en 5
- Vermenigvuldiging met 6
-Voeg nullen toe aan het begin en het einde van de figuur om te vermenigvuldigen met 6.
-Tel bij elk cijfer de helft van zijn buurman rechts op, maar als het cijfer oneven is, tel er 5 bij op.
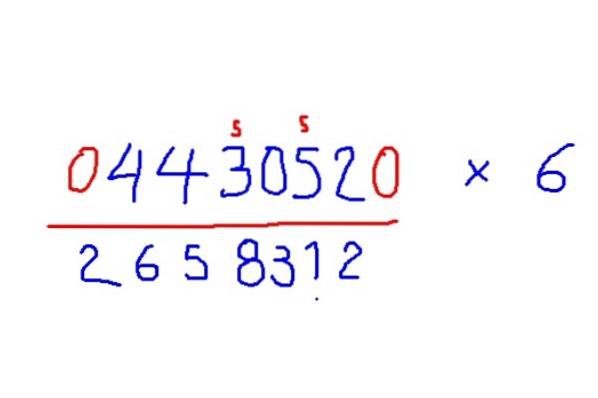
- Vermenigvuldiging met 7
-Voeg nullen toe aan het begin en einde van het getal dat u wilt vermenigvuldigen.
-Verdubbel elk cijfer en voeg de onderste hele helft van de buurman toe, maar als het cijfer oneven is, voeg dan 5 toe.
Voorbeeld van vermenigvuldiging met 7
-Vermenigvuldig 3412 met 7
-Het resultaat is 23884. Om de regels toe te passen, wordt aanbevolen om eerst de oneven cijfers te herkennen en een kleine 5 erboven te plaatsen om te onthouden dat u dit cijfer bij het resultaat moet optellen..
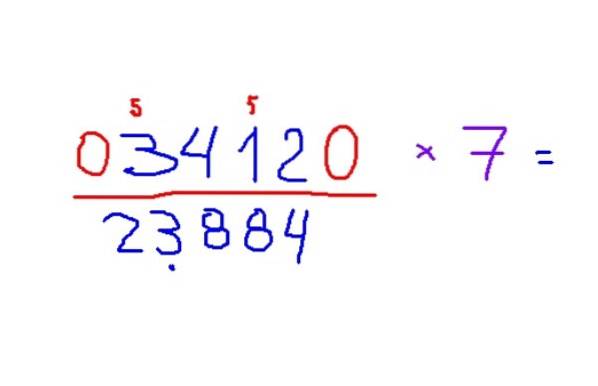
- Vermenigvuldiging met 5
-Voeg nullen toe aan het begin en einde van het getal dat u wilt vermenigvuldigen.
-Plaats onder elk cijfer de onderste hele helft van de buurman aan de rechterkant, maar als het cijfer oneven is, voeg dan 5 toe.
Voorbeeld vermenigvuldiging met 5
Vermenigvuldig 256413 met 5
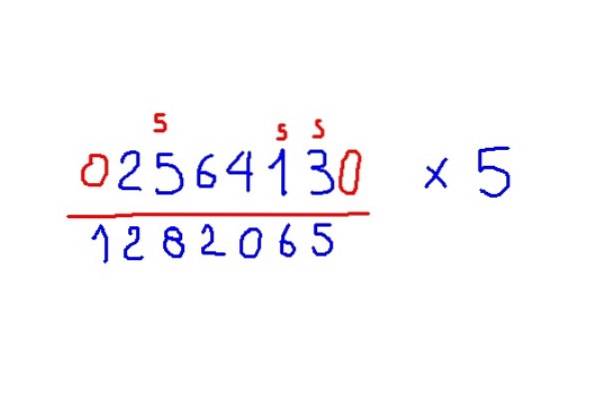
Regels voor producten door 9
-Aan het begin wordt een nul toegevoegd en aan het einde van de figuur een nul, die met negen moet worden vermenigvuldigd.
-Het eerste cijfer aan de rechterkant wordt verkregen door het overeenkomstige cijfer van het te vermenigvuldigen getal van 10 af te trekken.
-Vervolgens wordt het volgende cijfer afgetrokken van 9 en wordt de buurman opgeteld.
-De vorige stap wordt herhaald totdat we de nul van het vermenigvuldigtal bereiken, waar we 1 aftrekken van de buurman en het resultaat onder nul wordt gekopieerd..
Voorbeeld van vermenigvuldiging met 9
Vermenigvuldig 8769 met 9:
087690 x 9 =
--
78921
Operaties
10 - 9 = 1
(9-6) + 9 = 1twee (de twee en duurt 1)
(9-7) + 1 + 6 =9
(9-8) +7 =8
(8-1) = 7
Vermenigvuldiging met 8, 4, 3 en 2
-Voeg nullen toe aan het begin en einde van het getal dat u wilt vermenigvuldigen.
-Trek voor het eerste cijfer van rechts af van 10 en het resultaat wordt verdubbeld.
-Voor de volgende cijfers: aftrekken van 9, het resultaat wordt verdubbeld en de buurman wordt opgeteld.
-Trek bij het bereiken van nul 2 af van de buurman aan de rechterkant.
- Vermenigvuldiging met 8
Voorbeeld van vermenigvuldiging met 8
-Vermenigvuldig 789 met 8
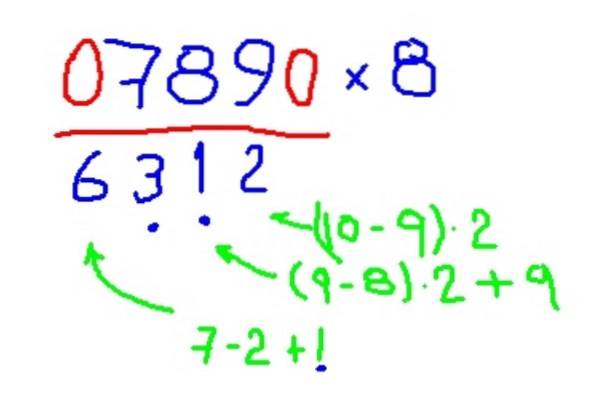
- Vermenigvuldiging met 4
-Voeg nullen rechts en links van het vermenigvuldigingspunt toe.
-Trek het corresponderende cijfer van de eenheid af van 10 door 5 op te tellen als het een oneven cijfer is.
-Trek elk cijfer van het vermenigvuldigtal af van 9 in het formulier, tel de helft van de buurman rechts op en als het een oneven cijfer is, tel er dan 5 bij op.
-Wanneer u de nul van het begin van het vermenigvuldigtal bereikt, plaatst u de helft van de buur min één.
Voorbeeld van vermenigvuldiging met 4
Vermenigvuldig 365187 x 4
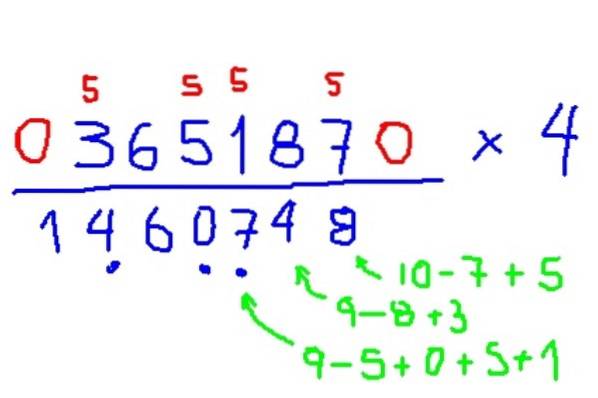
- Vermenigvuldiging met 3
-Voeg nul toe aan elk uiteinde van het vermenigvuldigtal.
-Trek 10 min het cijfer van de enen af en tel er 5 bij op als het een oneven cijfer is.
-Trek voor de andere cijfers 9 af, verdubbel het resultaat, tel de helft van de buur op en tel er 5 bij op als deze oneven is..
-Wanneer u de nul van de koptekst bereikt, plaatst u de onderste gehele helft van de buur min 2.
Voorbeeld van vermenigvuldiging met 3
Vermenigvuldig 2588 met 3

- Vermenigvuldiging met 2
-Voeg nullen toe aan de uiteinden en verdubbel elk cijfer, als het groter is dan 10, voegt u een aan het volgende toe.
Voorbeeld vermenigvuldiging met 2
Vermenigvuldig 2374 met 2
023740 x 2
04748
Vermenigvuldig met samengestelde cijfers
De bovenstaande regels zijn van toepassing, maar de resultaten worden naar links weergegeven op basis van het aantal plaatsen dat overeenkomt met tientallen, honderden, enzovoort. Laten we naar het volgende voorbeeld kijken:
Oefening
Vermenigvuldig 37654 met 498
0376540 x 498
301232 liniaal voor 8
338886 regel voor 9
150616 liniaal voor 4
18751692 eindbedrag
Referenties
- Cutler, Ann. 1960 Het Trachtenberg-snelheidssysteem van elementaire wiskunde. Doubleday & CO, NY.
- Dialnet. Snel eenvoudig wiskundig systeem. Hersteld van: dialnet.com
- Wiskundige hoek. Snelle vermenigvuldiging volgens de Trachtenberg-methode. Hersteld van: rinconmatematico.com
- Het Trachtenberg Speed System of Basic Mathematics. Hersteld van: trachtenbergspeedmath.com
- Wikipedia. Trachtenberg-methode. Hersteld van: wikipedia.com



Niemand heeft nog op dit artikel gereageerd.