
Willekeurige steekproefmethodologie, voordelen, nadelen, voorbeelden
De willekeurige steekproeven het is de manier om een statistisch representatieve steekproef uit een bepaalde populatie te selecteren. Onderdeel van het principe dat elk element in de steekproef dezelfde kans moet hebben om geselecteerd te worden.
Een trekking is een voorbeeld van willekeurige steekproeven, waarbij elk lid van de deelnemerspopulatie een nummer krijgt toegewezen. Om de nummers te kiezen die overeenkomen met de loterijprijzen (de steekproef) wordt een willekeurige techniek gebruikt, bijvoorbeeld het uit een mailbox halen van de nummers die op identieke kaarten zijn geregistreerd.
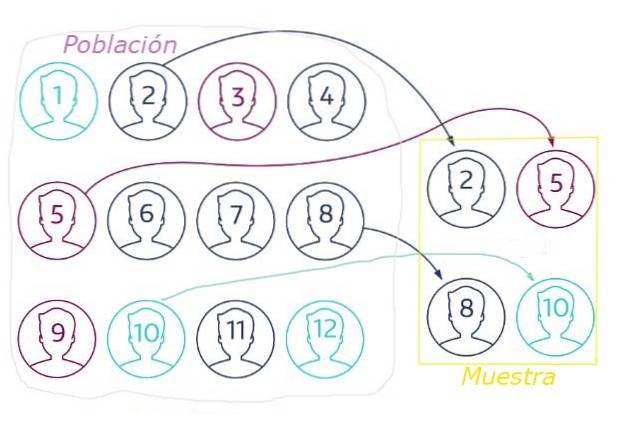
Bij aselecte steekproeven is het essentieel om de steekproefomvang goed te kiezen, omdat een niet-representatieve steekproef van de populatie door statistische fluctuaties tot verkeerde conclusies kan leiden..
Artikel index
- 1 De steekproefomvang
- 1.1 Case 1: de omvang van de populatie is onbekend
- 1.2 Case 2: de omvang van de populatie is bekend
- 2 voorbeelden
- 2.1 Enquêtes en vragenlijsten
- 2.2 Kwaliteitscontrole
- 3 voordelen
- 4 nadelen
- 5 Oefening opgelost
- 6 referenties
De grootte van de steekproef
Er zijn formules om de juiste grootte van een steekproef te bepalen. De belangrijkste factor om te overwegen is of de populatiegrootte bekend is of niet. Laten we eens kijken naar de formules om de steekproefomvang te bepalen:
Case 1: de omvang van de populatie is onbekend
Als de populatiegrootte N onbekend is, is het mogelijk om een steekproef van voldoende grootte n te selecteren om te bepalen of een bepaalde hypothese waar of onwaar is.
Hiervoor wordt de volgende formule gebruikt:
n = (Ztwee p q) / (E.twee
Waar:
-p is de kans dat de hypothese waar is.
-q is de kans dat dit niet zo is, dus q = 1 - p.
-E is de relatieve foutmarge, bijvoorbeeld een fout van 5% heeft een marge E = 0,05.
-Z heeft te maken met de mate van vertrouwen die de studie vereist.
In een gestandaardiseerde (of genormaliseerde) normale verdeling heeft een betrouwbaarheidsniveau van 90% Z = 1,645, omdat de kans dat het resultaat tussen -1,645σ en + 1,645σ ligt 90% is, waarbij σ de standaarddeviatie is.
Betrouwbaarheidsniveaus en hun bijbehorende Z-waarden
1. - 50% betrouwbaarheidsniveau komt overeen met Z = 0,675.
2. - 68,3% betrouwbaarheidsniveau komt overeen met Z = 1.
3. - 90% betrouwbaarheidsniveau is gelijk aan Z = 1.645.
4. - 95% betrouwbaarheidsniveau komt overeen met Z = 1,96
5. - 95,5% betrouwbaarheidsniveau komt overeen met Z = 2.
6. - 99,7% betrouwbaarheidsniveau is gelijk aan Z = 3.
Een voorbeeld waarin deze formule kan worden toegepast, is een onderzoek om het gemiddelde gewicht van kiezelstenen op een strand te bepalen.
Het is duidelijk dat het niet mogelijk is om alle kiezelstenen op het strand te bestuderen en te wegen, dus het is raadzaam om een zo willekeurig mogelijke steekproef te nemen met het juiste aantal elementen..

Case 2: de omvang van de populatie is bekend
Als het aantal N elementen waaruit een bepaalde populatie (of universum) bestaat bekend is, is dit de formule als u een statistisch significante steekproef van grootte n wilt selecteren door middel van een eenvoudige willekeurige steekproef:
n = (Ztweep q N) / (N Etwee + Ztweep q)
Waar:
-Z is de coëfficiënt die is gekoppeld aan het betrouwbaarheidsniveau.
-p is de kans op succes van de hypothese.
-q is de faalkans in de hypothese, p + q = 1.
-N is de grootte van de totale populatie.
-E is de relatieve fout van het studieresultaat.
Voorbeelden
De methode om de monsters te extraheren, hangt sterk af van het type onderzoek dat moet worden gedaan. Daarom heeft willekeurige steekproeven een oneindig aantal toepassingen:
Enquêtes en vragenlijsten
Bij telefonische enquêtes worden bijvoorbeeld de te raadplegen personen gekozen met behulp van een generator voor willekeurige getallen die van toepassing is op de onderzochte regio..
Als u een vragenlijst wilt toepassen op de werknemers van een groot bedrijf, dan kunt u een beroep doen op de selectie van de respondenten via hun personeelsnummer of identiteitskaartnummer.
Dit nummer moet ook willekeurig worden gekozen, bijvoorbeeld met behulp van een generator voor willekeurige getallen.

QA
In het geval dat het onderzoek betrekking heeft op onderdelen die door een machine zijn vervaardigd, moeten onderdelen willekeurig worden gekozen, maar uit batches die op verschillende tijdstippen van de dag of op verschillende dagen of weken zijn vervaardigd..
Voordeel
Eenvoudige willekeurige bemonstering:
- Het maakt het mogelijk de kosten van een statistisch onderzoek te verlagen, aangezien het niet nodig is om de totale populatie te bestuderen om statistisch betrouwbare resultaten te verkrijgen, met de gewenste betrouwbaarheidsniveaus en het vereiste foutenpercentage voor het onderzoek..
- Voorkom vooringenomenheid: aangezien de keuze van de te bestuderen elementen volledig willekeurig is, weerspiegelt het onderzoek getrouw de kenmerken van de populatie, hoewel slechts een deel ervan werd bestudeerd.
Nadelen
- De methode is niet geschikt in gevallen waarin u de voorkeuren in verschillende groepen of bevolkingslagen wilt weten.
In dit geval verdient het de voorkeur om vooraf de groepen of segmenten te bepalen waarop het onderzoek moet worden uitgevoerd. Als de strata of groepen eenmaal zijn gedefinieerd, dan, als het gepast is, willekeurige steekproeven op elk van hen toe te passen..
- Het is zeer onwaarschijnlijk dat er informatie zal worden verkregen over minderheidssectoren, waarvan het soms nodig is om hun kenmerken te kennen.
Als het bijvoorbeeld gaat om het maken van een campagne voor een duur product, is het noodzakelijk om de voorkeuren van de rijkste minderheidssectoren te kennen.
Oefening opgelost
We willen de voorkeur van de populatie voor een bepaald coladrankje bestuderen, maar er is geen eerdere studie bij deze populatie waarvan de omvang onbekend is..
Anderzijds moet de steekproef representatief zijn met een minimaal betrouwbaarheidsniveau van 90% en moeten de conclusies een foutpercentage van 2% hebben..
-Hoe de steekproefomvang te bepalen n?
-Wat zou de steekproefomvang zijn als de foutenmarge wordt versoepeld tot 5%??
Oplossing
Omdat de populatiegrootte onbekend is, wordt de bovenstaande formule gebruikt om de steekproefomvang te bepalen:
n = (Ztweep q) / (E.twee
We gaan ervan uit dat er een gelijke kans op voorkeur (p) is voor ons merk frisdrank als op niet-voorkeur (q), dan is p = q = 0,5.
Aan de andere kant, aangezien het resultaat van het onderzoek een foutpercentage van minder dan 2% moet hebben, is de relatieve fout E 0,02.
Ten slotte levert een Z-waarde = 1.645 een betrouwbaarheidsniveau van 90% op.
Samenvattend hebben we de volgende waarden:
Z = 1.645
p = 0,5
q = 0,5
E = 0,02
Met deze gegevens wordt de minimale steekproefomvang berekend:
n = (1.645twee 0,5 0,5) / (0,02twee) = 1691,3
Dit betekent dat het onderzoek met de vereiste foutenmarge en met het gekozen betrouwbaarheidsniveau een steekproef van respondenten van ten minste 1692 personen moet hebben, gekozen door middel van een eenvoudige willekeurige steekproef..
Ga je van een foutmarge van 2% naar 5%, dan is de nieuwe steekproefomvang:
n = (1.645twee 0,5 0,5) / (0,05twee) = 271
Dat is een aanzienlijk lager aantal individuen. Concluderend: de steekproefomvang is erg gevoelig voor de gewenste foutmarge in het onderzoek..
Referenties
- Berenson, M. 1985. Statistieken voor management en economie, concepten en toepassingen. Redactioneel Interamericana.
- Statistieken. Willekeurige bemonstering. Genomen uit: encyclopediaeconomica.com.
- Statistieken. Bemonstering. Hersteld van: Estadistica.mat.uson.mx.
- Verkenbaar. Willekeurige bemonstering. Hersteld van: explorable.com.
- Moore, D. 2005. Toegepaste basisstatistieken. 2e. Editie.
- Netquest. Willekeurige bemonstering. Hersteld van: netquest.com.
- Wikipedia. Statistische steekproeven. Hersteld van: en.wikipedia.org


Niemand heeft nog op dit artikel gereageerd.