
Ingeschreven hoek van een cirkeldefinitie, stellingen, voorbeelden
De ingeschreven hoek van een cirkel Het is er een die zijn top op de omtrek heeft en zijn stralen zijn secans of raken eraan. Als gevolg hiervan zal de ingeschreven hoek altijd convex of vlak zijn..
In figuur 1 zijn verschillende hoeken weergegeven die zijn ingeschreven in hun respectieve omtrek. De hoek ∠EDF wordt ingeschreven door zijn top D op de omtrek te hebben en zijn twee stralen [DE) en [DF) die de omtrek snijden.
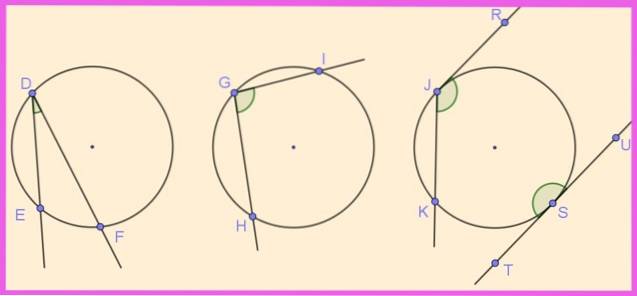
Evenzo is de hoek ∠HGI ingeschreven, omdat het zijn top op de omtrek heeft en de zijkanten eraan snijden.
De hoeken ∠KJR en ∠UST zijn ook op de omtrek gegraveerd. De eerste heeft een secanszijde en de andere raaklijn, terwijl de tweede twee zijden heeft die raken aan de omtrek en een vlakke ingeschreven hoek vormen (180º).
Sommige auteurs noemen de halfgeschreven hoek dat een van de zijden raakt aan de omtrek, maar in dit artikel wordt het als ingeschreven beschouwd..
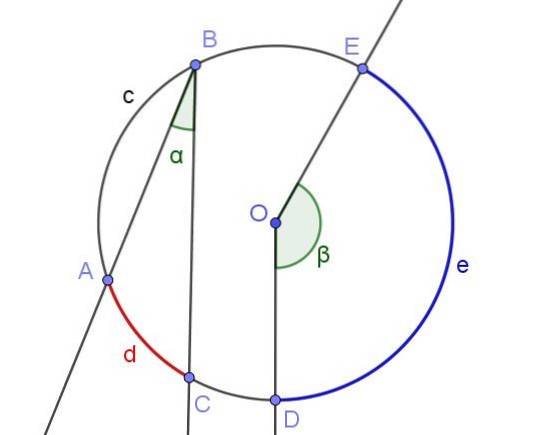
Elke ingeschreven hoek definieert of onderspant een bijbehorende boog. In figuur 2 bijvoorbeeld, onderspant de ingeschreven hoek ∠ABC de boog A⌒C met lengte d.
Dezelfde afbeelding toont de hoek ∠DOE, die niet in de omtrek is ingeschreven omdat de top niet de omtrek heeft, maar in het midden O.
Artikel index
- 1 Centrale hoek
- 2 stellingen
- 2.1 - Stelling 1 (Ingeschreven hoek en centrale hoek)
- 2.2 - Stelling 2
- 2.3 - Stelling 3
- 3 voorbeelden
- 3.1 - Voorbeeld 1
- 3.2 - Voorbeeld 2
- 4 referenties
Centrale hoek
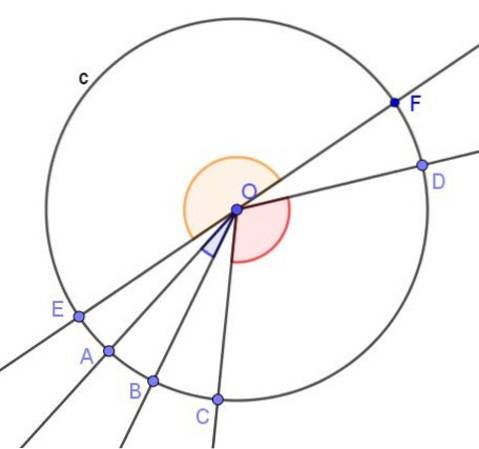
Naast de ingeschreven hoek, in een omtrek de centrale hoek, dat is degene waarvan de top in het midden van de omtrek ligt en waarvan de zijkanten de omtrek snijden.
De maat in radialen van een centrale hoek is het quotiënt tussen de ononderbroken boog, dat wil zeggen de omtrekboog tussen de zijden van de hoek en de straal van de omtrek.
Als de omtrek unitair is (van straal 1), dan is de lengte van de boog in dezelfde straaleenheden de maat van de hoek in radialen.
En als de hoekmaat in graden vereist is, wordt de maat in radialen vermenigvuldigd met de factor 180º / π.
Hoekmeetinstrumenten gebruiken altijd een centrale hoek en de lengte van de boog die daardoor wordt ingesloten, wordt direct in graden gekalibreerd. Dit betekent dat wanneer een hoek wordt gemeten, op de achtergrond de lengte van de boog wordt gemeten die wordt ingesloten door de centrale hoek.
Stellingen
- Stelling 1 (Ingeschreven hoek en centrale hoek)
De maat van een ingeschreven hoek is de helft van de maat van de centrale hoek, als beide hoeken dezelfde boog insluiten.
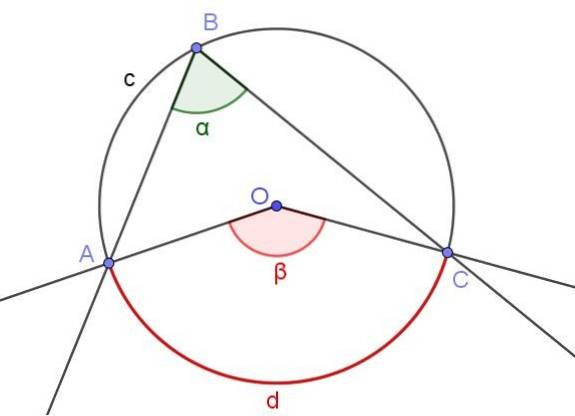
In figuur 4 worden twee hoeken ∠ABC en ∠AOC getoond, die dezelfde omtrekboog A⌒C snijden.
Als de maat van de ingeschreven hoek α is, dan is de maat β van de centrale hoek tweemaal de maat van de ingeschreven hoek (β = 2 α) omdat beide dezelfde boog van maat d insluiten..
Demonstratie 1a
Om stelling 1 te bewijzen, zullen we beginnen met het tonen van enkele specifieke gevallen, totdat we het algemene geval bereiken.
Veronderstel een ingeschreven hoek, waarbij een van zijn zijden door het midden van de omtrek gaat, zoals weergegeven in figuur 5.
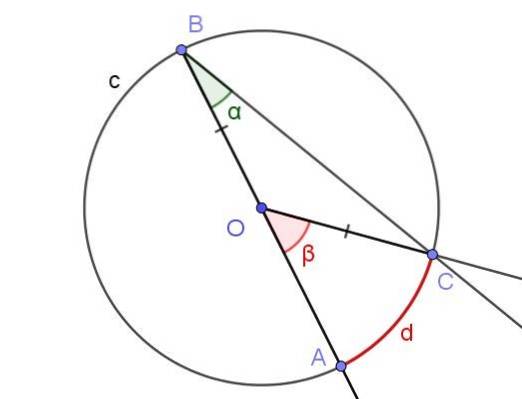
In dit geval wordt de gelijkbenige driehoek COB gevormd, aangezien [OC] = [OB].
In een gelijkbenige driehoek zijn de hoeken naast de basis gelijk, dus ∠BCO = ∠ABC = α. Aan de andere kant ∠COB = 180º - β.
Gezien de som van de interne hoeken van de driehoek COB, hebben we:
α + α + (180º - β) = 180º
Hieruit volgt dat 2 α = β, of wat equivalent is: α = β / 2. Dit valt samen met wat stelling 1 stelt: de maat van de ingeschreven hoek is de helft van de centrale hoek, als beide hoeken hetzelfde akkoord insluiten [AC].
Demonstratie 1b
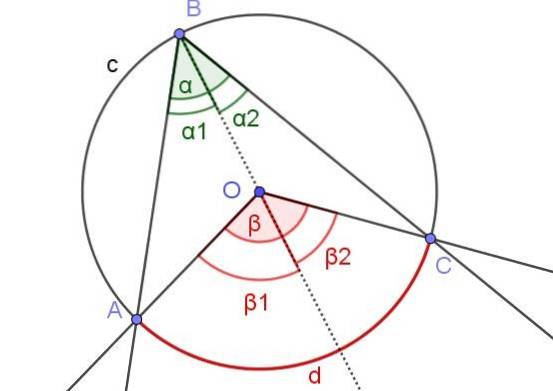
In dit geval hebben we een ingeschreven hoek ∠ABC, waarin het middelpunt O van de omtrek binnen de hoek ligt.
Om in dit geval stelling 1 te bewijzen, wordt de hulpstraal [BO) getekend, zodat we twee ingeschreven hoeken ∠ABO en ∠OBC naast de straal hebben.
Evenzo hebben we de centrale hoeken β1 en βtwee grenzend aan genoemde straal. Op deze manier hebben we dezelfde situatie als in bewijs 1a, dus kan worden gesteld dat αtwee = βtwee / 2 en α1 = β1 /twee. Omdat α = α1 + αtwee en β = β1 + βtwee daarom volgt hieruit dat α = α1 + αtwee = β1 / 2 + βtwee / 2 = (β1 + βtwee) / 2 = β / 2.
Concluderend α = β / 2, die voldoet aan stelling 1.
- Stelling 2
Als twee of meer ingeschreven hoeken dezelfde boog insluiten, hebben ze dezelfde maat.
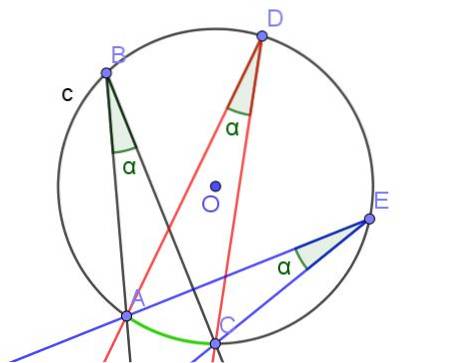
- Stelling 3
De ingeschreven hoeken die akkoorden van dezelfde maat insluiten, zijn gelijk.
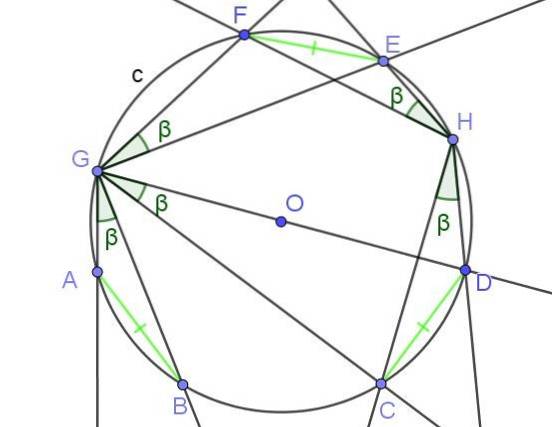
Voorbeelden
- voorbeeld 1
Laat zien dat de ingeschreven hoek die de diameter onderspant een rechte hoek is.
Oplossing
De centrale hoek ∠AOB die bij de diameter hoort, is een vlakke hoek, waarvan de maat 180º is.
Volgens stelling 1 heeft elke hoek in de omtrek die hetzelfde akkoord insluit (in dit geval de diameter), als maat de helft van de centrale hoek die hetzelfde akkoord insluit, wat in ons voorbeeld 180º / 2 = 90º is..
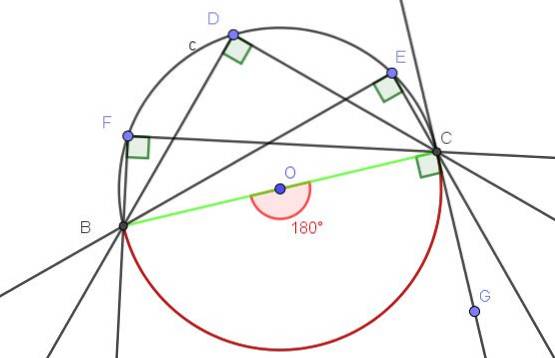
- Voorbeeld 2
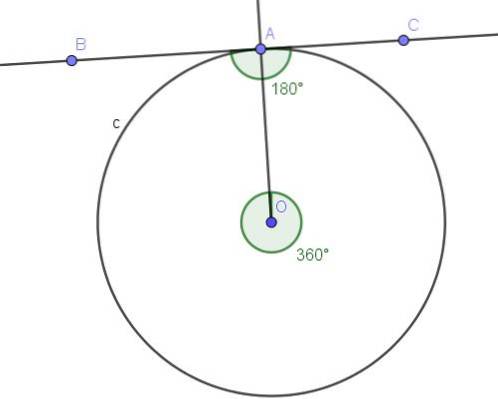
De lijn (BC) die A raakt aan de omtrek C, bepaalt de ingeschreven hoek ∠BAC (zie figuur 10).
Controleer of aan stelling 1 van de ingeschreven hoeken is voldaan.
Oplossing
De hoek ∠BAC is ingeschreven omdat het hoekpunt zich op de omtrek bevindt en de zijkanten [AB) en [AC) de omtrek raken, dus aan de definitie van de ingeschreven hoek is voldaan.
Aan de andere kant, de ingeschreven hoek ∠BAC onderspant de boog A, A, die de volledige omtrek is. De centrale hoek die de boog A⌒A onderspant, is een convexe hoek waarvan de maat de volledige hoek is (360º).
De ingeschreven hoek die de hele boog onderspant, meet de helft van de bijbehorende centrale hoek, dat wil zeggen ∠BAC = 360º / 2 = 180º.
Met al het bovenstaande wordt geverifieerd dat dit specifieke geval voldoet aan stelling 1.
Referenties
- Baldor. (1973). Geometrie en trigonometrie. Centraal-Amerikaans cultureel hoofdartikel.
- E. A. (2003). Geometrie-elementen: met oefeningen en geometrie van het kompas. Universiteit van Medellin.
- Geometrie 1e ESO. Hoeken op de omtrek. Hersteld van: edu.xunta.es/
- Alle wetenschap. Voorgestelde oefeningen van hoeken in de omtrek. Hersteld van: francesphysics.blogspot.com
- Wikipedia. Ingeschreven hoek. Hersteld van: es.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.