
Definitie en kenmerken van nulhoeken, voorbeelden, oefeningen
De null-hoek Het is er een waarvan de maat 0 is, zowel in graden als in radialen of een ander systeem voor hoekmeting. Daarom mist het breedte of opening, zoals gevormd tussen twee parallelle lijnen..
Hoewel de definitie ervan eenvoudig genoeg klinkt, is de nulhoek erg handig in veel natuurkundige en technische toepassingen, evenals in navigatie en ontwerp..
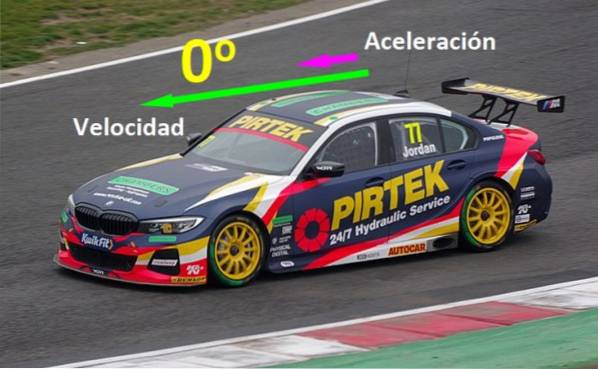
Er zijn fysieke grootheden die parallel moeten worden uitgelijnd om bepaalde effecten te bereiken: als een auto in een rechte lijn op een snelweg rijdt en zijn snelheidsvector invoert v en zijn versnellingsvector naar er is 0º, de auto beweegt steeds sneller, maar als de auto remt, is de acceleratie tegengesteld aan de snelheid (zie figuur 1).
De volgende afbeelding toont verschillende soorten hoeken, inclusief de nulhoek naar rechts. Zoals te zien is, mist de hoek van 0 ° breedte of opening..

Artikel index
- 1 Voorbeelden van nulhoeken
- 1.1 - Effecten van de nulhoek op fysieke grootheden
- 2 oefeningen
- 2.1 - Oefening 1
- 2.2 - Oefening 2
- 3 referenties
Voorbeelden van nulhoeken
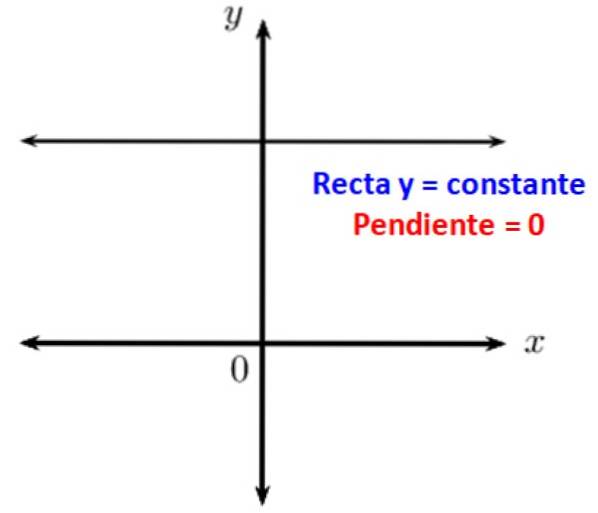
Van parallelle lijnen is bekend dat ze een nulhoek met elkaar vormen. Als je een horizontale lijn hebt, is deze evenwijdig aan de x-as van het Cartesiaans coördinatensysteem, daarom is de helling ten opzichte daarvan 0. Met andere woorden, horizontale lijnen hebben een helling van nul.
Ook de trigonometrische verhoudingen van de nulhoek zijn 0, 1 of oneindig. Daarom is de nulhoek aanwezig in veel fysieke situaties waarin bewerkingen met vectoren voorkomen. Deze redenen zijn:
-sin 0º = 0
-cos 0º = 1
-tg 0º = 0
-sec 0º = 1
-cosec 0º → ∞
-ctg 0º → ∞
En ze zullen nuttig zijn om enkele voorbeelden te analyseren van situaties waarin de aanwezigheid van de nulhoek een fundamentele rol speelt:
- Effecten van de nulhoek op fysieke grootheden
Vector toevoeging
Als twee vectoren parallel zijn, is de hoek ertussen nul, zoals te zien is in figuur 4a hierboven. In dit geval wordt de som van beide uitgevoerd door de een na de ander te plaatsen en is de grootte van de somvector de som van de grootte van de bijlagen (figuur 4b).

Als twee vectoren parallel zijn, is de hoek ertussen nul, zoals te zien is in figuur 4a hierboven. In dit geval wordt de som van beide uitgevoerd door de een na de ander te plaatsen en is de grootte van de somvector de som van de grootte van de bijlagen (figuur 4b)
Het koppel of koppel
Het koppel of koppel veroorzaakt de rotatie van een lichaam. Het hangt af van de grootte van de uitgeoefende kracht en hoe deze wordt uitgeoefend. Een heel representatief voorbeeld is de sleutel in de afbeelding.
Om het beste draai-effect te bereiken, wordt de kracht loodrecht op de handgreep van de sleutel uitgeoefend, omhoog of omlaag, maar er wordt geen rotatie verwacht als de kracht parallel is aan de handgreep..
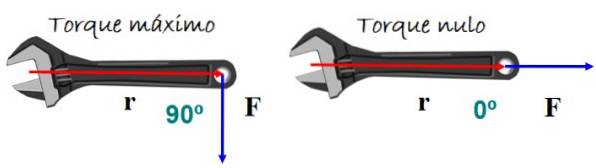
Wiskundig koppel τ wordt gedefinieerd als het kruisproduct of kruisproduct tussen vectoren r (positievector) en F. (krachtvector) uit figuur 5:
τ = r X F.
De grootte van het koppel is:
τ = r F zonde θ
Waar θ de hoek tussen is r Y F.. Als sin θ = 0 is het koppel nul, in dit geval θ = 0º (of ook 180º).
Flux van elektrisch veld
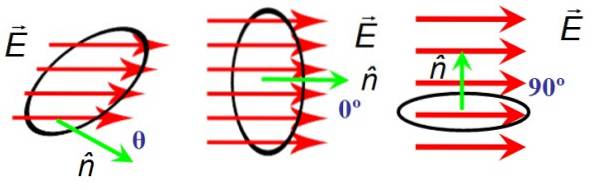
De flux van het elektrische veld is een scalaire grootte die afhangt van de intensiteit van het elektrische veld en van de oriëntatie van het oppervlak waar het doorheen gaat..
In figuur 6 is er een cirkelvormig oppervlak van gebied A waar de elektrische veldlijnen doorheen gaan EN. De oriëntatie van het oppervlak wordt gegeven door de normaalvector n. Links vormen het veld en de normaalvector een willekeurige scherpe hoek θ, in het midden vormen ze een nulhoek met elkaar, en rechts staan ze loodrecht.
Wanneer EN Y n loodrecht staan, de veldlijnen kruisen het oppervlak niet en daarom is de flux nul, terwijl de hoek tussen EN Y n nul is, lopen de lijnen volledig door het oppervlak.
De elektrische veldflux wordt aangeduid met de Griekse letter Φ (lees "fi"), en de definitie voor een uniform veld zoals in de afbeelding ziet er als volgt uit:
Φ = ENnNAAR
Het punt in het midden van beide vectoren geeft het puntproduct of puntproduct aan, dat alternatief als volgt wordt gedefinieerd:
Φ = ENnA = EAcosθ
De vetgedrukte pijlen en de pijlen boven de letter zijn middelen om onderscheid te maken tussen een vector en de grootte ervan, die wordt aangegeven met normale letters. Aangezien cos 0 = 1, is de flux maximaal wanneer EN Y n ze zijn parallel.
Opleiding
- Oefening 1
Twee krachten P. Y Q werken gelijktijdig op een puntobject X, beide krachten vormen aanvankelijk een hoek θ tussen hen in. Wat gebeurt er met de grootte van de resulterende kracht als θ afneemt tot nul?
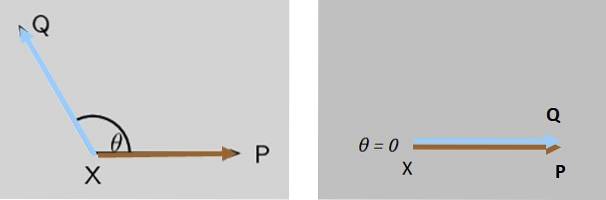
Oplossing
De grootte van de resulterende kracht Q + P. neemt geleidelijk toe totdat het maximaal is wanneer Q Y P. zijn volledig parallel (figuur 7 rechts).
- Oefening 2
Geef aan of de nulhoek een oplossing is van de volgende goniometrische vergelijking:
cos 2x = 1 + 4 sin x
Oplossing
Een trigonometrische vergelijking is er een waarin het onbekende deel uitmaakt van het argument van een trigonometrische verhouding. Om de voorgestelde vergelijking op te lossen, is het handig om de formule voor de cosinus van de dubbele hoek te gebruiken:
cos 2x = costwee x - zondetwee X
Omdat op deze manier het argument aan de linkerkant wordt X in plaats van 2x. Dan:
costwee x - zondetwee x = 1 + 4sin x
Aan de andere kant costwee x + zondetwee x = 1, dus:
costwee x - zondetwee x = costwee x + zondetwee x + 4sen x
De term costwee x is geannuleerd en blijft:
- sentwee x = zondetwee x + 4sen x → - 2sentwee x - 4senx = 0 → 2sentwee x + 4senx = 0
Nu wordt de volgende variabele wijziging aangebracht: sinx = u en de vergelijking wordt:
2utwee + 4u = 0
2u (u + 4) = 0
Wiens oplossingen zijn: u = 0 en u = -4. Als we de verandering teruggeven, zouden we twee mogelijkheden hebben: sin x = 0 en sinx = -4. Deze laatste oplossing is niet haalbaar, omdat de sinus van elke hoek tussen -1 en 1 ligt, dus houden we het eerste alternatief over:
zonde x = 0
Daarom is x = 0º een oplossing, maar elke hoek waarvan de sinus 0 is, werkt ook, die ook 180º (π radialen), 360º (2 π radialen) en de respectievelijke negatieven kunnen zijn.
De meest algemene oplossing van de goniometrische vergelijking is: x = kπ waarbij k = 0, ± 1, ± 2, ± 3,…. k een geheel getal.
Referenties
- Baldor, A. 2004. Vlak- en ruimtegeometrie met trigonometrie. Publicaciones Cultural S.A. de C.V. Mexico.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 3. Deeltjessystemen. Bewerkt door Douglas Figueroa (USB).
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 5. Elektrische interactie. Bewerkt door Douglas Figueroa (USB).
- OnlineMathLearning. Soorten hoeken. Hersteld van: onlinemathlearning.com.
- Zill, D. 2012. Algebra, trigonometrie en analytische meetkunde. McGraw Hill Interamericana.



Niemand heeft nog op dit artikel gereageerd.