
Hoeken in de omtrektypen, eigenschappen, opgeloste oefeningen
Gebeld omtrek hoeken die waarin sommige van zijn elementen zijn of elkaar snijden op een gegeven omtrek. Onder hen zijn de volgende:
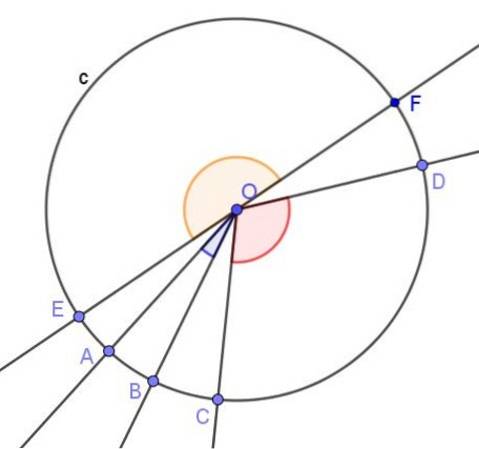
1. - Het centrale hoek, waarvan de top zich in het midden van de omtrek bevindt en de zijkanten ervan secans zijn, zoals we zien in de volgende afbeelding:

2.- Het ingeschreven hoek, waarvan de top is op de omtrek en de zijkanten zijn secans of raken aan de omtrek.
3.- Buitenhoek, waarvan de top buiten de omtrek ligt, maar de zijkanten zijn secans of raken aan de omtrek.
4. - Het binnenhoek, met het hoekpunt binnen de omtrek en de zijkanten ervan secans.
Al deze hoeken hebben bepaalde relaties met elkaar en dit leidt ons naar belangrijke eigenschappen tussen de hoeken die bij een bepaalde cirkel horen.
Artikel index
- 1 Eigenschappen
- 1.1 - Centrale hoek
- 1.2 - Ingeschreven hoek
- 1.3 - Buitenhoek
- 1.4 - Binnenhoek
- 2 Opgeloste oefeningen
- 2.1 - Oefening 1
- 2.2 - Oefening 2
- 3 referenties
Eigendommen
- Centrale hoek
De centrale hoek wordt gedefinieerd als die waarvan de top in het midden van de omtrek ligt en de zijkanten de omtrek snijden.
De maat in radialen van een centrale hoek is het quotiënt tussen de ononderbroken boog, dat wil zeggen de omtrekboog tussen de zijden van de hoek en de straal van de omtrek.
Als de omtrek unitair is, dat wil zeggen straal 1, dan is de maat van de centrale hoek de lengte van de boog, die overeenkomt met het aantal radialen.
Als u de maat van de centrale hoek in graden wilt, vermenigvuldigt u de maat in radialen met de factor 180º / π.
Hoekmeetinstrumenten, zoals de gradenboog en goniometer, gebruiken altijd een centrale hoek en de lengte van de onderspannen boog.
Ze zijn gekalibreerd in sexagesimale graden, wat betekent dat wanneer er een hoek mee wordt gemeten, op de achtergrond de lengte van de boog wordt gemeten die wordt ingesloten door de centrale hoek..
Eigendom
De maat van een centrale hoek in radialen is gelijk aan de lengte van de insluitende of onderscheppende boog gedeeld door de lengte van de straal.
- Ingeschreven hoek
De ingeschreven hoek van een cirkel is er een die zijn top op de omtrek heeft en zijn stralen zijn secans of raken eraan..
De eigenschappen zijn:
Eigendommen
-De ingeschreven hoek is convex of vlak.
-Wanneer een ingeschreven hoek dezelfde boog snijdt als de centrale hoek, is de maat van de eerste hoek de helft van die van de tweede..
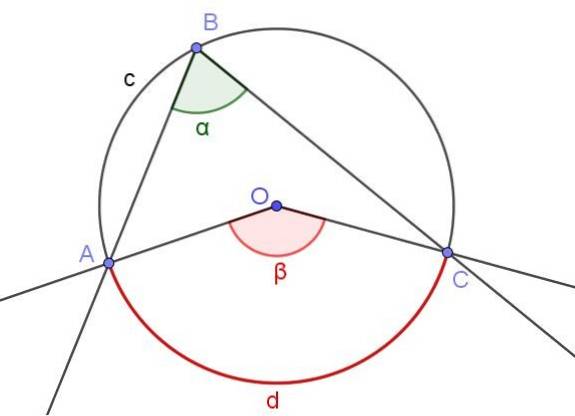
Figuur 3 toont twee hoeken ∠ABC en ∠AOC die dezelfde omtrekboog A⌒C snijden.
Als de maat van de ingeschreven hoek α is, dan is de maat β van de centrale hoek tweemaal de maat van de ingeschreven hoek (β = 2 α) omdat beide dezelfde boog van maat d insluiten..
- Buitenhoek
Het is de hoek waarvan het hoekpunt buiten de omtrek ligt en elk van zijn zijden snijdt de omtrek op een of meer punten.
Eigendom
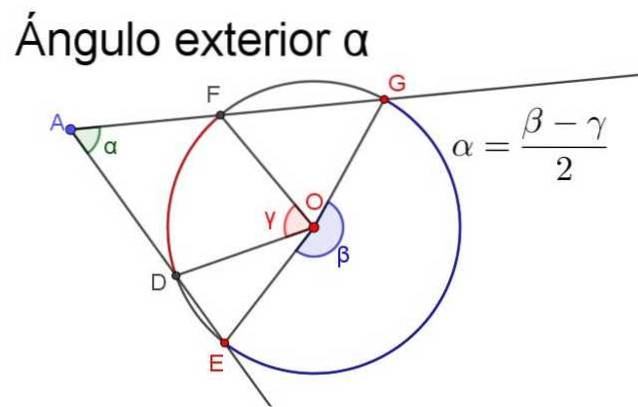
-De maat is gelijk aan het halve verschil (of verschil gedeeld door 2) van de centrale hoeken die dezelfde bogen onderscheppen.
Om ervoor te zorgen dat de meting positief is, moet het semi-verschil altijd die van de grootste centrale hoek minus de maat van de kleinste centrale hoek zijn, zoals geïllustreerd in de volgende afbeelding.
- Binnenhoek
De binnenhoek is degene waarvan de top binnen de omtrek ligt en de zijkanten de omtrek snijden.
Eigendom
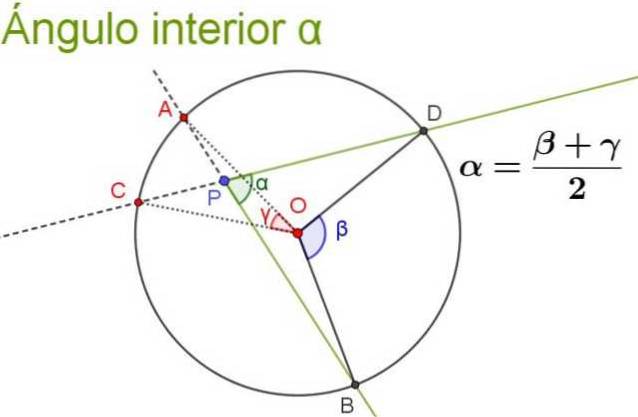
Zijn maat is gelijk aan de halve som van de centrale hoek die dezelfde boog onderspant, plus de centrale hoek die dezelfde boog onderspant als de uitbreidingshoek (dit is de binnenhoek gevormd door de stralen complementair aan die van de oorspronkelijke binnenhoek ).
De volgende afbeelding illustreert en verduidelijkt de eigenschap van de binnenhoek.
Opgeloste oefeningen
- Oefening 1
Veronderstel een ingeschreven hoek waarin een van zijn zijden door het middelpunt van de cirkel gaat, zoals weergegeven in figuur 6. De straal van de cirkel is OA = 3 cm en de boog d heeft een lengte van π / 2 cm. Bepaal de waarde van de hoeken α en β.
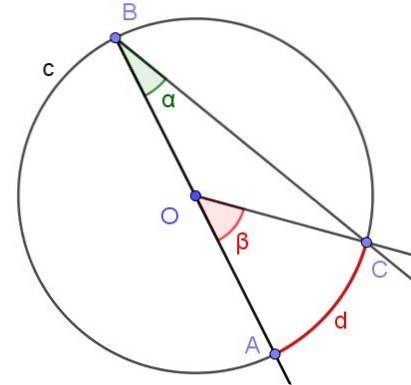
Oplossing
In dit geval wordt de gelijkbenige driehoek COB gevormd, aangezien [OC] = [OB]. In een gelijkbenige driehoek zijn de hoeken naast de basis gelijk, dus ∠BCO = ∠ABC = α. Aan de andere kant ∠COB = 180º - β. Gezien de som van de interne hoeken van de driehoek COB, hebben we:
α + α + (180º - β) = 180º
Hieruit volgt dat 2 α = β, of wat equivalent is α = β / 2, waarmee de eigenschap (3) van de vorige paragraaf wordt bevestigd, dat de maat van de ingeschreven hoek de helft is van de centrale hoek, als beide hoeken tussen hetzelfde akkoord [AC].
Nu gaan we verder met het bepalen van de numerieke waarden: de hoek β is centraal en de maat in radialen is het quotiënt tussen de boog d en de straal r = OA, dus de maat is:
β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.
Aan de andere kant was al gezegd dat α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º.
- Oefening 2
In figuur 7 zijn de hoeken α1 en βtwee ze hebben dezelfde maat. Verder is de hoek β1 meet 60º. Bepaal de hoeken β en α.
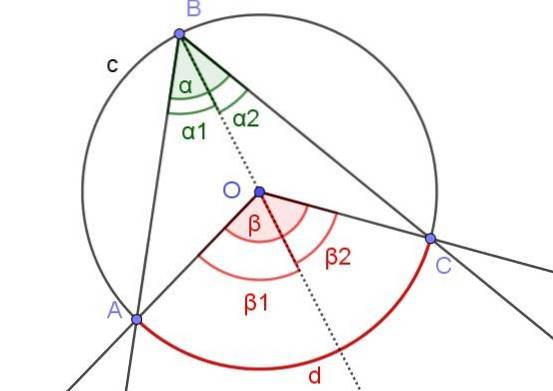
Oplossing
In dit geval hebben we een ingeschreven hoek ∠ABC waarin het middelpunt O van de omtrek binnen de hoek ligt.
Vanwege de eigenschap (3) hebben we αtwee = βtwee / 2 en α1 = β1 /twee. Wat:
α = α1 + αtwee en β = β1 + βtwee
Daarom volgt hieruit dat:
α = α1 + αtwee = β1 / 2 + βtwee / 2 = (β1 + βtwee) / 2 = β / 2.
Dat wil zeggen, volgens de eigenschappen:
α = β / 2
Omdat ons is verteld dat β1 = 60º dan:
α1 = β1 / 2 = 60º / 2 = 30º.
Ze vertellen ons ook dat α1 = βtwee dus het volgt dat:
βtwee = 30º.
De hoek β resulteert:
β1 + βtwee = 60º + 30º = 90º.
En aangezien α = β / 2, dan:
α = 90º / 2 = 45º.
Tot slot:
β = 90º en α = 45º.
Referenties
- Baldor, A. 1973. Meetkunde en driehoeksmeting. Centraal-Amerikaanse culturele uitgeverij.
- E. A. 2003. Geometrie-elementen: met oefeningen en kompasgeometrie. Universiteit van Medellin.
- Geometrie 1e ESO. Hoeken op de omtrek. Hersteld van: edu.xunta.es.
- Alle wetenschap. Problemen met hoeken in de omtrek opgelost. Hersteld van: francesphysics.blogspot.com
- Wikipedia. Ingeschreven hoek. Hersteld van: es.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.