
Ontwikkelde notatie wat het is, voorbeelden en oefeningen
De uitgebreide notatie is er een waarin een numeriek getal wordt uitgedrukt als een som waarin rekening wordt gehouden met de positiewaarde van elk cijfer waaruit het getal bestaat.
Als u bijvoorbeeld een cijfer als 2345 schrijft, heeft elk cijfer daarin een positionele hiërarchie. Als je van het uiterst rechtse cijfer naar links leest, groeit de hiërarchie of waarde.
In het getal 2345 staat het cijfer 5 voor vijf eenheden, het cijfer 4 staat voor vier tienen, de 3 komt overeen met de derde positie van links naar rechts en daarom staat de 3 voor drie honderd, tenslotte staat de 2 voor tweeduizend. Met andere woorden, in ontwikkelde of uitgebreide notatie, wordt het cijfer 2345 als volgt geschreven:
2345 = 2 duizenden + 3 honderden + 4 tientallen + 5 enen
Maar het kan ook als volgt worden uitgedrukt:
2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.
Ook het getal 2345 kan worden geschreven als de som van machten van 10:
2345 = 2 x 10 ^ 3 + 3 x 10 ^ 2 + 4 x 10 ^ 1 + 5 x 10 ^ 0
Waar de circumflex ^ betekent verhogen tot de aangegeven exponent. Bijvoorbeeld 10 ^ 3 = 10 x 10 x 10 = 1000. Een andere manier om de exponenten te schrijven is door een superscript te gebruiken:
2345 = 2 x 103 + 3 x 10twee + 4 x 101 + 5x100
Artikel index
- 1 Positienummeringssysteem
- 1.1 Breuk- of decimale getallen
- 2 Voorbeelden van uitgebreide notatie
- 2.1 Voorbeeld 1
- 2.2 Voorbeeld 2
- 3 Oefeningen van uitgebreide notatie
- 3.1 Oefening 1
- 3.2 Oefening 2
- 3.3 Oefening 3
- 3.4 Oefening 6
- 4 referenties
Positioneel nummeringssysteem
Het Arabische cijfersysteem zijn de cijfers die dagelijks in de overgrote meerderheid van continenten en landen van de wereld worden gebruikt. Arabische cijfers zijn een basis 10-systeem omdat tien symbolen of grafemen worden gebruikt om elk nummer te schrijven. Deze tien symbolen zijn:
0 1 2 3 4 5 6 7 8 9
Met slechts één van deze symbolen kunnen cijfers van nul tot negen worden uitgedrukt. Om cijfers groter dan negen uit te drukken, wordt het positiesysteem in basis tien gebruikt. Het getal 10 is een tien en nul eenheden. Het nummer 11 is een tien en een eenheid. Het getal 123 (honderd drieëntwintig) is honderd, twee tienen en drie. Geschreven in de vorm van machten van tien zal het getal 123 zijn:
1 × 10 ^ 2 + 2 × 10 ^ 1 + 3 × 10 ^ 0
Waar:
10 ^ 2 = 10 x 10 = 100
10 ^ 1 = 10
10 ^ 0 = 1.
Met dit voorbeeld is het duidelijk dat de positie van het cijfer uiterst rechts positie 0 is en het aantal eenheden vertegenwoordigt, die van het tweede cijfer van rechts naar links positie 1 en het aantal tientallen is, het derde cijfer (van rechts links) heeft positie 2 en vertegenwoordigt de honderden.
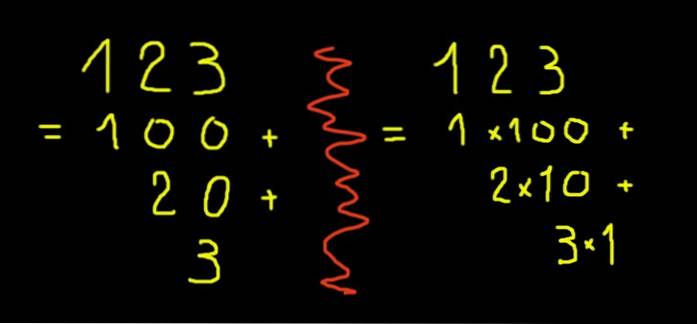
Breuk- of decimale getallen
Met het decimale positiesysteem is het ook mogelijk om getallen of cijfers weer te geven die kleiner zijn dan de eenheid of die groter zijn dan de eenheid, maar geen gehele getallen, dat wil zeggen, ze hebben fracties van de eenheid.
Om in het Arabische decimale systeem de breuk ½, dat wil zeggen de helft van de eenheid, weer te geven, wordt geschreven:
½ = 0,5
Om tot deze uitdrukking in ons basis 10-systeem te komen, zijn de volgende bewerkingen impliciet uitgevoerd:
1- De teller en de noemer worden vermenigvuldigd met 5 om de equivalente breuk 5/10 = 1/2 te hebben.
2- Delen door 10 is gelijk aan vermenigvuldigen met de macht in grondtal tien met exponent min één (10 ^ -1), dat wil zeggen 5/10 = 5 × 10 ^ -1.
3- De negatieve exponent geeft aan hoe vaak het aangegeven cijfer is verplaatst of naar rechts is gepositioneerd ten opzichte van de eenheidspositie, in ons geval zou dit 0,5 zijn.
4- ½ = 0,5 in uitgebreide notatie wordt als volgt geschreven:
0,5 = 0x10 ^ 0 + 5 × 10 ^ -1
Waarbij 10 ^ -1 = 0,1 een tiende is (de breuk die overeenkomt met de eenheid verdeeld in 10 gelijke delen).
Op deze manier komt het getal 0,5 overeen met vijf tienden, maar het getal 0,05 komt overeen met 5 honderdsten en 0,005 met 5 duizendsten.
Voorbeelden van uitgebreide notatie
voorbeeld 1
Gegeven het cijfer 40201 in standaardnotatie, converteert u het naar uitgebreide notatie.
Oplossing:
4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201
Voorbeeld 2
Schrijf de breuk ¾ in uitgebreide notatie.
Oplossing:
In dit geval heb je driekwart van de eenheid.
3/4 = 15/20 = 75/100 = 0,75 = 7/10 + 5/100 =
7 × 10 ^ -1 + 5 × 10 ^ -2.
Met woorden gezegd, het zou er als volgt uitzien:
De breuk ¾ komt overeen met zeven tienden plus vijf honderdsten.
Oefeningen met uitgebreide notatie
Oefening 1
Zeg met woorden de uitgebreide uitdrukking van het cijfer 40201 uit voorbeeld 1.
Oplossing:
De ontwikkelde notatie ziet er als volgt uit:
40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1
Dat in de taal van woorden wordt gezegd:
Vier tienduizenden, plus nul duizenden, plus tweehonderd, plus nul tienen, plus één eenheid.
Oefening 2
Druk de vorige figuur in woorden uit en verdeel de overeenkomstige zin in uitgebreide vorm.
Oplossing:
Het cijfer 40201 wordt in woorden als volgt uitgedrukt:
Veertigduizend tweehonderd één
De vorige zin kan worden ontwikkeld als:
40 × 1000 + 2 × 100 + 1
Men kan zeggen dat de manier om de cijfers uit te spreken een semi-ontwikkelde manier is om ze uit te drukken.
Oefening 3
Schrijf in uitgevouwen vorm het cijfer 7/3.
Oplossing:
Het is een getal dat wordt uitgedrukt als een onjuiste breuk, aangezien als de teller groter is dan de noemer, het getal groter is dan de eenheid.
Deze oneigenlijke fractie kan worden ontleed als de som van de fracties 6/3 + 1/3. De eerste van de breuken resulteert in een geheel getal 2, terwijl 1/3 = 0,333333, waarbij het cijfer 3 oneindig wordt herhaald. Dus de uitgebreide decimale uitdrukking van het cijfer 7/3 zal altijd een geschatte uitdrukking zijn:
7/3 = 2 + 1/3 ≃ 2 + 0,333 = 2 + 3 × 10 ^ -1 + 3 × 10 ^ -2 + 3 × 10 ^ -3.
Oefening 6
Schrijf in standaardnotatie en vervolgens in uitgebreide vorm het nummer: Drieëntwintig miljard tweehonderd vijftig miljoen vijfhonderd zesentwintig duizend driehonderd vijfentwintig en drie drieëntwintig duizendsten.
Oplossing:
Houd er rekening mee dat a miljard is het equivalent van een miljard. Het woord miljard het werd in 1995 door de Koninklijke Spaanse Academie aanvaard op verzoek van wijlen de Venezolaanse president Rafael Caldera, een lid van de Venezolaanse taalacademie. In dat geval wordt het cijfer voor de oefening in standaardnotatie als volgt geschreven:
23,2501526,325,023
23 miljard + 250 miljoen + 526 duizend + 325 eenheden + 23 duizendsten.
23 × 10 ^ 9 + 250 × 10 ^ 6 + 526 × 10 ^ 3 + 325 × 10 ^ 0 + 23 × 10 ^ -3
Ten slotte wordt de figuur in uitgebreide notatie geschreven:
2 × 10 ^ 10 + 3 × 10 ^ 9 + 2 × 10 ^ 8 + 5 × 10 ^ 7 + 0x10 ^ 6 + 5 × 10 ^ 5 + 2 × 10 ^ 4 + 6 × 10 ^ 3 + 3 × 10 ^ 2 + 2 × 10 ^ 1 + 5 × 10 ^ 0 + 0x10 ^ -1 + 2 × 10 ^ -2 + 3 × 10 ^ -3.
Referenties
- Khan Academy. Plaatswaardediagrammen. Hersteld van: es.khanacademy.org
- Khan Academy. Schrijf een getal in uitgevouwen vorm (video). Hersteld van: es.khanacademy.org
- Ifrah, Geoges (1998): Universal history of figures. Espasa Calpe S.A.
- Wikipedia. Positionele notatie. Hersteld van: es.wikipedia.com
- Wikipedia. Miljard. Hersteld van: es.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.