
Papomudas Hoe ze op te lossen en oefeningen
De papomuda's is een procedure voor het oplossen van algebraïsche uitdrukkingen. De afkortingen geven de volgorde van prioriteit van de bewerkingen aan: haakjes, machten, vermenigvuldigen, delen, optellen en aftrekken. Door dit woord te gebruiken, kunt u gemakkelijk de volgorde onthouden waarin u een uitdrukking moet oplossen die uit verschillende bewerkingen bestaat.
Over het algemeen kunnen in numerieke uitdrukkingen verschillende rekenkundige bewerkingen samen worden gevonden, zoals optellen, aftrekken, vermenigvuldigen en delen, die ook breuken, machten en wortels kunnen zijn. Om ze op te lossen, is het noodzakelijk om een procedure te volgen die garandeert dat de resultaten correct zijn..

Een rekenkundige uitdrukking die uit een combinatie van deze bewerkingen bestaat, moet worden opgelost volgens de volgorde van prioriteit, ook wel de hiërarchie van bewerkingen genoemd, die lang geleden in universele conventies is vastgelegd. Zo kunnen alle mensen dezelfde procedure volgen en hetzelfde resultaat behalen.
Artikel index
- 1 Kenmerken
- 2 Hoe ze op te lossen?
- 3 Toepassing
- 3.1 Uitdrukkingen die optellen en aftrekken bevatten
- 3.2 Uitdrukkingen die optellen, aftrekken en vermenigvuldigen bevatten
- 3.3 Uitdrukkingen met optellen, aftrekken, vermenigvuldigen en delen
- 3.4 Uitdrukkingen die optellen, aftrekken, vermenigvuldigen, delen en machten bevatten
- 3.5 Uitdrukkingen die groeperingssymbolen gebruiken
- 4 oefeningen
- 4.1 Eerste oefening
- 4.2 Tweede oefening
- 4.3 Derde oefening
- 5 referenties
Kenmerken
Papomudas is een standaardprocedure die de volgorde bepaalt die moet worden gevolgd bij het oplossen van een uitdrukking, die is samengesteld uit een combinatie van bewerkingen zoals optellen, aftrekken, vermenigvuldigen en delen..
Met deze procedure wordt de volgorde van prioriteit van een operatie vastgesteld in relatie tot de andere op het moment waarop ze zullen worden uitgevoerd; dat wil zeggen, elke operatie heeft een verschuiving of hiërarchisch niveau dat moet worden opgelost.
De volgorde waarin de verschillende bewerkingen van een uitdrukking moeten worden opgelost, wordt aangegeven door elk acroniem van het woord papomudas. U moet dus:
1- Pa: haakjes, haakjes of accolades.
2- Po: bevoegdheden en wortels.
3- Mu: vermenigvuldigingen.
4 - D: divisies.
5- A: toevoegingen of toevoegingen.
6- S: aftrekken of aftrekken.
Deze procedure wordt in het Engels ook wel PEMDAS genoemd; om dit woord gemakkelijk te onthouden, wordt geassocieerd met de zin: "P.lezen ENxcuse M.Y Door NAARunt Sbondgenoot”, Waarbij elke beginletter overeenkomt met een rekenkundige bewerking, op dezelfde manier als de papomuda's.
Hoe ze op te lossen?
Op basis van de hiërarchie die door de papomuda's is vastgesteld om de bewerkingen van een uitdrukking op te lossen, is het noodzakelijk om de volgende volgorde te vervullen:
- Alle bewerkingen binnen groeperingssymbolen, zoals haakjes, accolades, vierkante haken en breukstrepen, moeten eerst worden opgelost. Als er symbolen zijn binnen andere, moet u beginnen met rekenen van binnen naar buiten.
Deze symbolen worden gebruikt om de volgorde waarin de bewerkingen worden opgelost te veranderen, omdat wat erin zit altijd eerst moet worden opgelost..
- Dan zijn de krachten en wortels opgelost.
- Op de derde plaats zijn de vermenigvuldigingen en delingen opgelost. Deze hebben dezelfde volgorde van prioriteit; daarom, wanneer deze twee bewerkingen in een uitdrukking worden gevonden, moet degene die het eerst verschijnt, worden opgelost door de uitdrukking van links naar rechts te lezen.
- In de laatste plaats worden de optellingen en aftrekkingen opgelost, die ook dezelfde volgorde van prioriteit hebben en daarom degene die als eerste in de uitdrukking verschijnt, van links naar rechts gelezen, is opgelost.
- Bewerkingen mogen nooit gemengd worden wanneer ze van links naar rechts worden gelezen, de volgorde van prioriteit of hiërarchie die door de papomuda's is vastgesteld, moet altijd worden gevolgd..
Het is belangrijk om te onthouden dat het resultaat van elke bewerking in dezelfde volgorde moet worden geplaatst ten opzichte van de andere, en dat alle tussenliggende stappen moeten worden gescheiden door een teken totdat het eindresultaat is bereikt..
App
De papomudas-procedure wordt gebruikt als u een combinatie van verschillende operaties heeft. Rekening houdend met hoe ze worden opgelost, kan dit worden toegepast in:
Uitdrukkingen met optellen en aftrekken
Het is een van de eenvoudigste bewerkingen, omdat beide dezelfde prioriteitsvolgorde hebben, zodanig dat het moet worden opgelost, beginnend van links naar rechts in de uitdrukking; bijvoorbeeld:
22-15 + 8 +6 = 21.
Uitdrukkingen met optellen, aftrekken en vermenigvuldigen
In dit geval is de bewerking met de hoogste prioriteit vermenigvuldigen, waarna optellen en aftrekken wordt opgelost (wat het eerste is in de uitdrukking). Bijvoorbeeld:
6 4 - 10 + 8 6 - 16 + 10 6
= 24-10 + 48-16 + 60
= 106.
Uitdrukkingen met optellen, aftrekken, vermenigvuldigen en delen
In dit geval heb je een combinatie van alle bewerkingen. Je begint met het oplossen van de vermenigvuldiging en deling die een hogere prioriteit hebben, dan het optellen en aftrekken. Als je de uitdrukking van links naar rechts leest, wordt deze opgelost volgens zijn hiërarchie en positie binnen de uitdrukking; bijvoorbeeld:
7 + 10 13 - 8 + 40 ÷ 2
= 7 + 130 - 8 + 20
= 149.
Uitdrukkingen die optellen, aftrekken, vermenigvuldigen, delen en machten bevatten
In dit geval wordt een van de getallen verhoogd tot een macht, die binnen het prioriteitsniveau eerst moet worden opgelost, om vervolgens de vermenigvuldigingen en delingen op te lossen en tenslotte de optellingen en aftrekkingen:
4 + 4twee 12 - 5 + 90 ÷ 3
= 4 + 16 12 - 5 + 90 ÷ 3
= 4 + 192 - 5 + 30
= 221.
Net als de machten hebben ook de wortels de tweede rangorde; Daarom moeten in uitdrukkingen die ze bevatten, vermenigvuldigen, delen, optellen en aftrekken eerst worden opgelost:
5 8 + 20 ÷ √ 16
= 5 8 + 20 ÷ 4
= 40 + 5
= 45.
Uitdrukkingen die groeperingssymbolen gebruiken
Wanneer tekens zoals haakjes, accolades, haakjes en breukstrepen worden gebruikt, wordt wat erin staat als eerste opgelost, ongeacht de volgorde van prioriteit van de bewerkingen die het bevat in relatie tot die erbuiten, alsof het een aparte uitdrukking zal zijn :
14 ÷ 2 - (8 - 5)
= 14 ÷ 2 - 3
= 7 - 3
= 4.
Als er meerdere bewerkingen in staan, moeten deze in hiërarchische volgorde worden opgelost. Vervolgens worden de andere bewerkingen waaruit de uitdrukking bestaat, opgelost; bijvoorbeeld:
2 + 9 * (5 + 23 - 24 ÷ 6) - 1
= 2 + 9 * (5 + 8 - 4) - 1
= 2 + 9 * 9 - 1
= 2 + 81 - 1
= 82.
Sommige uitdrukkingen gebruiken groeperingssymbolen binnen andere, bijvoorbeeld wanneer het teken van een bewerking moet worden gewijzigd. In deze gevallen moet u beginnen met het oplossen van binnenuit; dat wil zeggen, het vereenvoudigen van de groeperingssymbolen die in het midden van een uitdrukking staan.
Over het algemeen is de volgorde om bewerkingen in deze symbolen op te lossen: eerst los wat tussen haakjes () staat, dan haakjes [] en als laatste de accolades .
90 - 3[12 + (54) - (4twee)]
= 90 - 3 [12 + 20 - 8]
= 90 - 3 24
= 90 - 72
= 18.
Opleiding
Eerste oefening
Zoek de waarde van de volgende uitdrukking:
twintigtwee + √ 225 - 155 + 130.
Oplossing
Door de papomuda's toe te passen, moeten eerst de krachten en wortels worden opgelost, en dan optellen en aftrekken. In dit geval behoren de eerste twee bewerkingen tot dezelfde volgorde, dus degene die het eerst wordt uitgevoerd, wordt opgelost, beginnend van links naar rechts:
twintigtwee + √ 225 - 155 + 130
= 400 + 15-155 + 130.
Vervolgens tel je op en trek je af, ook vanaf links beginnend:
400 + 15-155 + 130
= 390.
Tweede oefening
Zoek de waarde van de volgende uitdrukking:
[- (63 - 36) ÷ (8 6 ÷ 16)].
Oplossing
Het begint met het oplossen van de bewerkingen die tussen haakjes staan, volgens de hiërarchische volgorde die ze hebben volgens de papomuda's.
Eerst worden de machten van de eerste haakjes opgelost, daarna worden de bewerkingen van de tweede haakjes opgelost. Omdat ze tot dezelfde volgorde behoren, is de eerste bewerking van de uitdrukking opgelost:
[- (63 - 36) ÷ (8 6 ÷ 16)]
= [- (216 - 729) ÷ (8 6 ÷ 16)]
= [- (216 - 729) ÷ (48 ÷ 16)]
= [- (-513) ÷ (3)].
Omdat de bewerkingen tussen de haakjes al zijn opgelost, gaan we nu verder met de deling die een hogere hiërarchie heeft dan de aftrekking:
[- (-513) ÷ (3)] = [- (-171)].
Ten slotte geeft het haakje dat het minteken (-) scheidt van het resultaat, dat in dit geval negatief is, aan dat deze tekens moeten worden vermenigvuldigd. Het resultaat van de uitdrukking is dus:
[- (-171)] = 171.
Derde oefening
Zoek de waarde van de volgende uitdrukking:

Oplossing
U begint met het oplossen van de breuken die tussen haakjes staan:
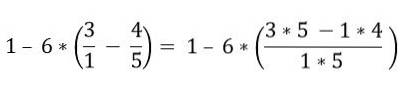
Binnen de haakjes zijn er verschillende bewerkingen. De vermenigvuldigingen worden eerst opgelost en daarna de aftrekkingen; In dit geval wordt de breukstreep beschouwd als een groeperingssymbool en niet als een divisie, daarom moeten de bewerkingen van het bovenste en onderste deel worden opgelost:
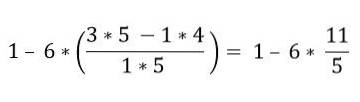
In hiërarchische volgorde moet de vermenigvuldiging worden opgelost:
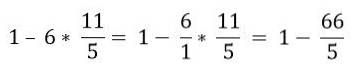
Ten slotte is het aftrekken opgelost:
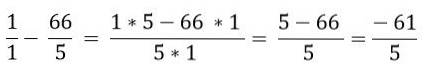
Referenties
- Aguirre, H. M. (2012). Financiële wiskunde. Cengage leren.
- Aponte, G. (1998). Fundamentals Of Basic Mathematics. Pearson Education.
- Cabanne, N. (2007). Didactiek van wiskunde.
- Carolina Espinosa, C. C. (2012). Hulpbronnen voor leeractiviteiten.
- Huffstetler, K. (2016). Het verhaal van de Order of Operations: Pemdas. Creëer ruimteonafhankelijk .
- Madore, B. (2009). GRE Math-werkboek. Barron's educatieve serie,.
- Molina, F. A. (s.f.). Azarquiel Project, Wiskunde: eerste cyclus. Azarquiel Groep.



Niemand heeft nog op dit artikel gereageerd.