
Frequentie waarschijnlijkheid concept, hoe het wordt berekend en voorbeelden
De frequentie waarschijnlijkheid is een subdefinitie binnen de studie van waarschijnlijkheid en zijn verschijnselen. Zijn studiemethode met betrekking tot gebeurtenissen en attributen is gebaseerd op grote hoeveelheden iteraties, waardoor hij de trend van elk op de lange termijn of zelfs bij oneindige herhalingen observeert..
Een envelop met gummies bevat bijvoorbeeld 5 gummen van elke kleur: blauw, rood, groen en geel. We willen de kans bepalen dat elke kleur eruit moet komen na een willekeurige selectie.

Het is vervelend om je voor te stellen een rubber eruit te halen, te registreren, terug te sturen, een rubber eruit te halen en hetzelfde enkele honderden of duizenden keren te herhalen. Misschien wilt u het gedrag zelfs na enkele miljoenen iteraties observeren.
Maar integendeel, het is interessant om te ontdekken dat na enkele herhalingen de verwachte kans van 25% niet volledig wordt gehaald, althans niet voor alle kleuren nadat 100 iteraties hebben plaatsgevonden..
Onder de benadering van de frequentiekans, zal de toewijzing van de waarden alleen plaatsvinden door de studie van vele iteraties. Op deze manier moet het proces bij voorkeur geautomatiseerd of geëmuleerd worden uitgevoerd en geregistreerd.
Meerdere stromen verwerpen de frequentiekans, omdat ze een gebrek aan empirie en betrouwbaarheid in de willekeurigheidscriteria bepleiten.
Artikel index
- 1 Hoe wordt de frequentiekans berekend?
- 1.1 Wet van grote aantallen
- 2 Andere benaderingen van waarschijnlijkheid
- 2.1 Logische theorie
- 2.2 Subjectieve theorie
- 3 Geschiedenis
- 3.1 Massaverschijnselen en repetitieve gebeurtenissen
- 3.2 Kenmerken
- 4 Voorbeeld
- 4.1 Referenties
Hoe wordt de frequentiekans berekend?
Door het experiment te programmeren in elke interface die een puur willekeurige iteratie kan bieden, kan men beginnen met het bestuderen van de frequentiekans van het fenomeen met behulp van een tabel met waarden.
Het vorige voorbeeld is te zien vanuit de frequentiebenadering:
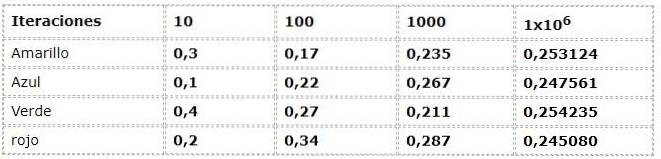
De numerieke gegevens komen overeen met de uitdrukking:
N (a) = aantal keren voorkomen / aantal iteraties
Waar N (a) staat voor de relatieve frequentie van de gebeurtenis "a"
"A" behoort tot de verzameling mogelijke uitkomsten of steekproefruimte Ω
Ω: rood, groen, blauw, geel
Een aanzienlijke spreiding wordt gewaardeerd in de eerste iteraties, bij het observeren van frequenties met tot 30% verschillen daartussen, wat een zeer hoog gegeven is voor een experiment dat theoretisch gebeurtenissen heeft met dezelfde mogelijkheid (Equiprobable).
Maar naarmate de iteraties groeien, lijken de waarden zich meer en meer aan te passen aan die van de theoretische en logische stroom.
Wet van de grote aantallen
Als een onverwachte overeenkomst tussen de theoretische en frequentiebenaderingen ontstaat de wet van grote getallen. Waarbij wordt vastgesteld dat na een aanzienlijk aantal iteraties de waarden van het frequentie-experiment de theoretische waarden naderen.
In het voorbeeld kun je zien hoe de waarden 0,250 naderen naarmate de iteraties toenemen. Dit fenomeen is elementair in de conclusies van veel probabilistische werken.

Andere benaderingen van waarschijnlijkheid
Naast de frequentie waarschijnlijkheid.
Logische theorie
Zijn benadering is gericht op de deductieve logica van verschijnselen. In het vorige voorbeeld is de kans om elke kleur te verkrijgen 25% op een gesloten manier. Dat wil zeggen, hun definities en axioma's houden geen rekening met vertragingen buiten hun bereik van probabilistische gegevens..
Subjectieve theorie
Het is gebaseerd op de kennis en eerdere overtuigingen die elk individu heeft over de verschijnselen en attributen. Uitspraken zoals "Het regent altijd met Pasen " Ze zijn het gevolg van een patroon van soortgelijke gebeurtenissen die eerder hebben plaatsgevonden.
Verhaal
Het begin van de implementatie ervan dateert uit de 19e eeuw, toen Venn het citeerde in verschillende van zijn werken in Cambridge, Engeland. Maar pas ver in de twintigste eeuw ontwikkelden en vormden 2 statistische wiskundigen de frequentie waarschijnlijkheid.
Een van hen was Hans Reichenbach, die zijn werk ontwikkelt in publicaties zoals "The Theory of Probability", gepubliceerd in 1949.
De andere was Richard Von Mises, die zijn werk verder ontwikkelde door middel van meerdere publicaties en voorstelde om waarschijnlijkheid als een wiskundige wetenschap te beschouwen. Dit concept was nieuw voor de wiskunde en zou een tijdperk van groei in de studie van wiskunde inluiden. frequentie waarschijnlijkheid.
Eigenlijk markeert deze gebeurtenis het enige verschil met de bijdragen van de generatie Venn, Cournot en Helm. Waar waarschijnlijkheid homoloog wordt aan wetenschappen zoals geometrie en mechanica.
< La teoría de las probabilidades trata con enorme verschijnselen en zich herhalende gebeurtenissen. Problemen waarbij óf dezelfde gebeurtenis keer op keer wordt herhaald, óf waarbij een groot aantal uniforme elementen tegelijkertijd betrokken is> Richard Von Mises
Enorme verschijnselen en zich herhalende gebeurtenissen
Er kunnen drie typen worden ingedeeld:
- Fysiek: ze gehoorzamen patronen van de natuur die verder gaan dan een toestand van willekeur. Bijvoorbeeld het gedrag van de moleculen van een element in een monster.
- Toeval - Je belangrijkste overweging is willekeur, zoals het herhaaldelijk gooien van een dobbelsteen.
- Biologische statistieken: selecties van proefpersonen op basis van hun kenmerken en attributen.
In theorie speelt de persoon die meet een rol in de probabilistische gegevens, omdat het zijn kennis en ervaringen zijn die deze waarde of voorspelling verwoorden..
In de frequentie waarschijnlijkheid de evenementen worden beschouwd als te behandelen collecties, waarbij het individu geen enkele rol speelt bij de schatting.
Attributen
In elk element komt een attribuut voor, dat afhankelijk van zijn aard variabel zal zijn. In het type fysisch fenomeen zullen de watermoleculen bijvoorbeeld verschillende snelheden hebben..
Bij de worp van de dobbelstenen kennen we de steekproefruimte Ω die de attributen van het experiment vertegenwoordigt.
Ω: 1, 2, 3, 4, 5, 6
Er zijn andere attributen, zoals even Ω zijnP. of oneven Ω zijnik
Ωp : 2, 4, 6
Ωik : 1, 3, 5
Die kunnen worden gedefinieerd als niet-elementaire attributen.
Voorbeeld
- We willen de frequentie berekenen van elke mogelijke optelling bij het werpen van twee dobbelstenen.
Hiervoor is een experiment geprogrammeerd waarbij in elke iteratie twee bronnen van willekeurige waarden tussen [1, 6] worden toegevoegd.
Gegevens worden in een tabel vastgelegd en trends in grote aantallen worden bestudeerd.
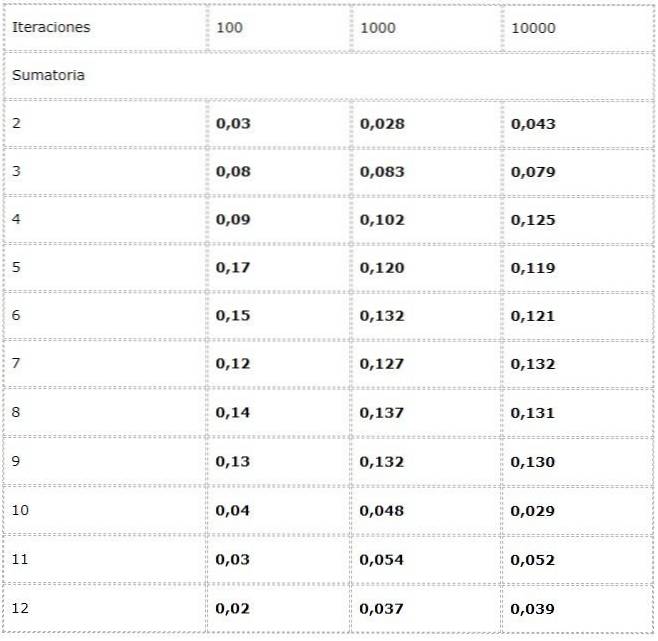
Opgemerkt wordt dat de resultaten aanzienlijk kunnen variëren tussen de iteraties. De wet van grote getallen is echter te zien in de schijnbare convergentie die in de laatste twee kolommen wordt gepresenteerd.
Referenties
- Statistieken en de evaluatie van bewijs voor forensische wetenschappers. Tweede druk. Colin G.G. Aitken. School voor wiskunde. De universiteit van Edinburgh, VK
- Wiskunde voor informatica. Eric Lehman. Google Inc.
F Thomson Leighton Departement Wiskunde en Computerwetenschappen en AI-laboratorium, Massachusetts Institute of Technology; Akamai Technologies - The Arithmetic Teacher, Volume 29. National Council of Teachers of Mathematics, 1981. University of Michigan.
- Getaltheorie leren en onderwijzen: onderzoek naar cognitie en instructie / bewerkt door Stephen R. Campbell en Rina Zazkis. Ablex publiceert 88 Post Road West, Westport CT 06881
- Bernoulli, J. (1987). Ars Conjectandi- 4ème partie. Rouen: IREM.


Niemand heeft nog op dit artikel gereageerd.