
Theoretische waarschijnlijkheid hoe je het kunt krijgen, voorbeelden, oefeningen
De theoretische waarschijnlijkheid (of Laplace) dat een gebeurtenis E optreedt die behoort tot een steekproefruimte S, waarin alle gebeurtenissen dezelfde kans van optreden hebben, wordt in wiskundige notatie gedefinieerd als: P (E) = n (E) / N (S)
Waar P (E) de kans is, gegeven als het quotiënt tussen het totale aantal mogelijke uitkomsten van de gebeurtenis E, die we n (E) noemen, gedeeld door het totale aantal N (S) mogelijke uitkomsten in de steekproefruimte S.

De theoretische kans is een reëel getal tussen 0 en 1, maar wordt vaak uitgedrukt als een percentage, in welk geval de kans een waarde tussen 0% en 100% zal zijn.
Het berekenen van de waarschijnlijkheid dat een gebeurtenis plaatsvindt, is erg belangrijk op veel gebieden, zoals handel, verzekeringsmaatschappijen, gokken en nog veel meer..
Artikel index
- 1 Hoe de theoretische kans te krijgen?
- 2 voorbeelden
- 2.1 Voorbeeld 1
- 2.2 Voorbeeld 2
- 3 oefeningen
- 3.1 Oefening 1
- 3.2 Oefening 2
- 3.3 Oefening 3
- 3.4 Oefening 4
- 4 referenties
Hoe de theoretische kans te krijgen?
Een illustratief geval is het geval van loterijen of loterijen. Stel dat er 1.000 loten worden uitgegeven om een smartphone te verloten. Omdat de trekking willekeurig plaatsvindt, heeft elk van de loten een gelijke kans om te winnen.
Om de kans te vinden dat een persoon die een kaartje koopt met het nummer 81 een winnaar is, volgt de volgende berekening van theoretische waarschijnlijkheid
P (1) = 1 / 1.000 = 0,001 = 0,1%
Het vorige resultaat wordt als volgt geïnterpreteerd: als de trekking oneindig vaak zou worden herhaald, zou elk 1.000 keer kaartje 81 gemiddeld één keer worden geselecteerd.
Als iemand om de een of andere reden alle tickets verwerft, is het zeker dat hij of zij de prijs wint. De kans om de prijs te winnen als je alle tickets hebt, wordt als volgt berekend:
P (1.000) = 1.000 / 1.000 = 1 = 100%.
Dat wil zeggen dat waarschijnlijkheid 1 of 100% betekent dat het volkomen zeker is dat dit resultaat zal optreden..
Als iemand 500 tickets bezit, zijn de kansen om te winnen of te verliezen hetzelfde. De theoretische kans om de prijs te winnen wordt in dit geval als volgt berekend:
P (500) = 500 / 1.000 = ½ = 0,5 = 50%.
Wie geen kaartje koopt, maakt geen kans om te winnen en zijn theoretische waarschijnlijkheid wordt als volgt bepaald:
P (0) = 0 / 1.000 = 0 = 0%
Voorbeelden
voorbeeld 1
Je hebt een muntje bij duur aan de ene kant en schild of stempel op de andere. Wanneer de munt wordt opgegooid, wat is dan de theoretische kans dat hij naar boven komt??
P (duur) = n (duur) / N ( gezicht + schild ) = ½ = 0,5 = 50%
Het resultaat wordt als volgt geïnterpreteerd: als er een groot aantal worpen werd gemaakt, zou er gemiddeld bij elke 2 worpen één met de kop omhoog komen.
In procenten uitgedrukt is de interpretatie van het resultaat dat het uitvoeren van een oneindig groot aantal worpen, gemiddeld van de 100 van de 50, zou resulteren in heads.
Voorbeeld 2
In een doos zitten 3 blauwe knikkers, 2 rode knikkers en 1 groene. Wat is de theoretische kans dat wanneer je een knikker uit de doos haalt, deze rood wordt??
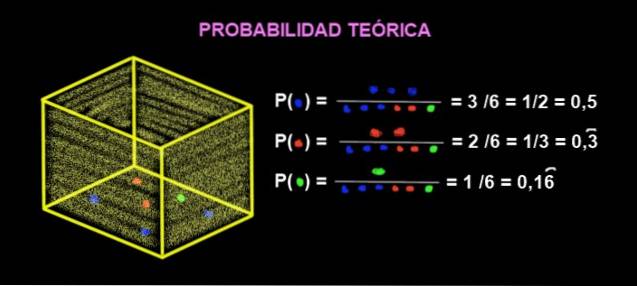
De kans dat het rood uitkomt is:
P (rood) = aantal gunstige gevallen / aantal mogelijke gevallen
Namelijk:
P (rood) = aantal rode knikkers / totaal aantal knikkers
Ten slotte is de kans dat een rode knikker wordt getrokken:
P (rood) = 2/6 = ⅓ = 0,3333 = 33,33%
Terwijl de kans dat bij het tekenen van een groene knikker is:
P (groen) = ⅙ = 0,1666 = 16,66%
Ten slotte is de theoretische kans om een blauwe knikker te verkrijgen bij een blinde extractie:
P (blauw) = 3/6 = ½ = 0,5 = 50%
Dat wil zeggen, voor elke 2 pogingen zal het resultaat blauw zijn in een van hen en een andere kleur in een andere poging, onder de vooronderstelling dat het geëxtraheerde marmer wordt vervangen en dat het aantal pogingen heel, heel groot is..
Opleiding
Oefening 1
Bepaal de kans dat bij het gooien van een dobbelsteen een waarde kleiner dan of gelijk aan 4 wordt verkregen.
Oplossing
Om de kans te berekenen dat deze gebeurtenis zich voordoet, wordt de definitie van theoretische kans toegepast:
P (≤4) = aantal gunstige gevallen / aantal mogelijke gevallen
P (≤5) = 5/6 = = 83,33%
Oefening 2
Zoek de kans dat er bij twee opeenvolgende worpen van een normale zeszijdige dobbelsteen 5 twee keer worden gegooid.
Oplossing
Om deze oefening te beantwoorden is het handig om een tafel te maken om alle mogelijkheden te laten zien. Het eerste cijfer geeft het resultaat van de eerste dobbelsteen aan en het tweede het resultaat van de andere.
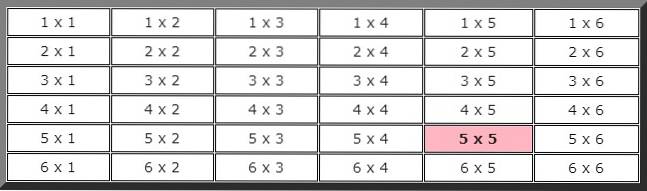
Om de theoretische kans te berekenen hebben we het totale aantal mogelijke gevallen nodig, in dit geval, zoals te zien is in de vorige tabel, zijn er 36 mogelijkheden.
Ook als we de tabel observeren, kan worden afgeleid dat het aantal gevallen dat gunstig is voor het evenement dat in de twee opeenvolgende lanceringen uitkomt 5 slechts 1 is, gemarkeerd met kleur, daarom is de kans dat deze gebeurtenis zich voordoet:
P (5 x 5) = 1/36.
Dit resultaat had ook kunnen worden bereikt met behulp van een van de eigenschappen van theoretische waarschijnlijkheid, die stelt dat de gecombineerde waarschijnlijkheid van twee onafhankelijke gebeurtenissen het product is van hun individuele kansen..
In dit geval is de kans dat de eerste toss met 5 wordt gegooid ⅙. De tweede worp is volledig onafhankelijk van de eerste, daarom is de kans dat 5 wordt gegooid in de tweede ook ⅙. Dus de gecombineerde kans is:
P (5 × 5) = P (5) P (5) = (1/6) (1/6) = 1/36.
Oefening 3
Zoek de kans dat een getal kleiner dan 2 wordt gegooid bij de eerste worp en een getal groter dan 2 wordt gegooid bij de tweede.
Oplossing

Nogmaals, er moet een tabel met mogelijke gebeurtenissen worden samengesteld, waarin die waarin de eerste worp minder dan 2 was en in de tweede meer dan 2 zijn gemarkeerd..
In totaal zijn er 4 mogelijkheden op een totaal van 36. Dat wil zeggen, de kans op deze gebeurtenis is:
P (<2 ; >2) = 4/36 = 1/9 = 0,1111 = 11,11%
Met behulp van de kansrekening die luidt:
De kans op het optreden van twee onafhankelijke gebeurtenissen is gelijk aan het product van de individuele kansen.
Hetzelfde resultaat wordt verkregen:
P (<2) P(>2) = (1/6) (4/6) = 4/36 = 0,1111 = 11,11%
De waarde die met deze procedure wordt verkregen, valt samen met het vorige resultaat, door de theoretische of klassieke definitie van waarschijnlijkheid.
Oefening 4
Wat is de kans dat bij het gooien van twee dobbelstenen de som van de waarden 7 is.
Oplossing

Om in dit geval de oplossing te vinden is een tabel met mogelijkheden opgesteld waarin de cases die voldoen aan de voorwaarde dat de som van de waarden 7 is, in kleur zijn aangegeven.
Als we naar de tabel kijken, kunnen 6 mogelijke gevallen worden geteld, dus de kans is:
P (I + II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%
Referenties
- Canavos, G. 1988. Waarschijnlijkheid en statistiek: toepassingen en methoden. Mcgraw heuvel.
- Devore, J. 2012. Waarschijnlijkheid en statistiek voor techniek en wetenschap. 8e. Editie. Cengage.
- Lipschutz, S. 1991. Schaum Series: Probability. Mcgraw heuvel.
- Obregón, I. 1989. Kansrekening. Redactioneel Limusa.
- Walpole, R. 2007. Waarschijnlijkheid en statistiek voor techniek en wetenschappen. Pearson.



Niemand heeft nog op dit artikel gereageerd.