De dynamisch programmeren is een algoritmemodel dat een complex probleem oplost door het op te splitsen in subproblemen, waarbij de resultaten worden opgeslagen om te voorkomen dat die resultaten opnieuw moeten worden berekend.
Dit schema wordt gebruikt wanneer u problemen heeft die kunnen worden onderverdeeld in vergelijkbare deelproblemen, zodat hun resultaten kunnen worden hergebruikt. Deze programmering wordt grotendeels gebruikt voor optimalisatie.
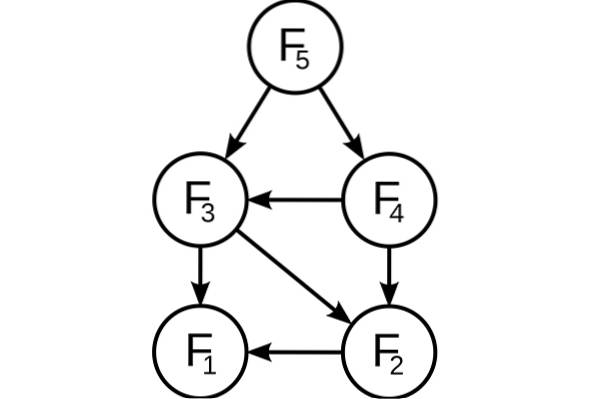
Voordat het beschikbare subprobleem wordt opgelost, zal het dynamische algoritme proberen de resultaten van de eerder opgeloste subproblemen te onderzoeken. Subprobleemoplossingen worden gecombineerd om tot de beste oplossing te komen.
In plaats van steeds hetzelfde subprobleem te berekenen, kunt u uw oplossing in een bepaald geheugen opslaan, wanneer u dit subprobleem voor het eerst tegenkomt. Als het weer verschijnt tijdens de oplossing van een ander subprobleem, wordt de oplossing die al in het geheugen is opgeslagen, gebruikt.
Dit is een geweldig idee om de geheugentijd vast te leggen, waarbij u door extra ruimte te gebruiken de tijd kunt verbeteren die nodig is om een oplossing te vinden..
Artikel index
De volgende essentiële kenmerken zijn waar u een probleem mee moet hebben voordat dynamisch programmeren kan worden toegepast:
Dit kenmerk drukt uit dat een optimalisatieprobleem kan worden opgelost door de optimale oplossingen van de secundaire problemen waaruit het bestaat te combineren. Deze optimale onderstructuren worden beschreven door middel van recursie.
In een grafiek wordt bijvoorbeeld een optimale substructuur gepresenteerd in het kortste pad r dat van een hoekpunt s naar een hoekpunt t gaat:
Dat wil zeggen, in dit kortste pad r kan elk tussenliggend hoekpunt i worden genomen. Als r echt de kortste route is, dan kan deze worden opgedeeld in de subroutes r1 (van s naar i) en r2 (van i naar t), zodanig dat dit op hun beurt de kortste routes zijn tussen de corresponderende hoekpunten.
Om de kortste routes te vinden, kan de oplossing daarom gemakkelijk recursief worden geformuleerd, wat het Floyd-Warshall-algoritme doet..
De subprobleemruimte moet klein zijn. Dat wil zeggen, elk recursief algoritme dat een probleem oplost, zal dezelfde subproblemen steeds opnieuw moeten oplossen, in plaats van nieuwe subproblemen te genereren..
Om bijvoorbeeld de Fibonacci-reeks te genereren, kan deze recursieve formulering worden beschouwd als: Fn = F (n-1) + F (n-2), met als basisscenario dat F1 = F2 = 1. Dan hebben we: F33 = F32 + F31 en F32 = F31 + F30.
Zoals je kunt zien, wordt F31 opgelost in de recursieve substructuren van zowel F33 als F32. Hoewel het totale aantal subproblemen erg klein is, zul je, als je een recursieve oplossing als deze toepast, dezelfde problemen steeds opnieuw oplossen..
Hiermee wordt rekening gehouden door dynamische programmering, dus het lost elk subprobleem slechts één keer op. Dit kan op twee manieren worden bereikt:
Als de oplossing voor een probleem recursief kan worden geformuleerd met behulp van de oplossing van zijn subproblemen, en als deze subproblemen elkaar overlappen, kunnen de oplossingen voor de subproblemen gemakkelijk worden onthouden of opgeslagen in een tabel.
Elke keer dat er naar een nieuwe subprobleemoplossing wordt gezocht, wordt de tabel gecontroleerd om te zien of deze eerder is opgelost. Als een oplossing is opgeslagen, wordt deze gebruikt in plaats van deze opnieuw te berekenen. Anders wordt het subprobleem opgelost en wordt de oplossing in de tabel opgeslagen.
Nadat de oplossing van een probleem recursief is geformuleerd in termen van zijn deelproblemen, zal het mogelijk zijn om het probleem op een oplopende manier te herformuleren: eerst zullen we proberen de deelproblemen op te lossen en hun oplossingen gebruiken om tot oplossingen te komen voor de grotere deelproblemen..
Dit gebeurt meestal ook in tabelvorm, waarbij iteratief oplossingen worden gegenereerd voor grotere en grotere deelproblemen door oplossingen te gebruiken voor kleinere deelproblemen. Als de waarden van F31 en F30 bijvoorbeeld al bekend zijn, kan de waarde van F32 direct worden berekend.
Een belangrijk kenmerk van een probleem dat dynamisch kan worden opgelost, is dat subproblemen elkaar moeten overlappen. Dit is wat dynamisch programmeren onderscheidt van de verdeel en heers-techniek, waarbij het niet nodig is om de eenvoudigste waarden op te slaan.
Het is vergelijkbaar met recursie, omdat bij het berekenen van de basisgevallen de uiteindelijke waarde inductief kan worden bepaald. Deze bottom-up benadering werkt goed wanneer een nieuwe waarde alleen afhangt van eerder berekende waarden.
Voor elk positief geheel getal "e" kan elk van de volgende drie stappen worden uitgevoerd.
- Trek 1 af van het getal. (e = e-1).
- Als het deelbaar is door 2, deel dan door 2 (als e% 2 == 0, dan e = e / 2).
- Als het deelbaar is door 3, deel dan door 3 (als e% 3 == 0, dan e = e / 3).
Op basis van de bovenstaande stappen moet het minimum aantal van deze stappen worden gevonden om e op 1 te brengen. Bijvoorbeeld:
- Als e = 1, resultaat: 0.
- Als e = 4, resultaat: 2 (4/2 = 2/2 = 1).
- Als e = 7, resultaat: 3 (7-1 = 6/3 = 2/2 = 1).
Je zou eraan kunnen denken om altijd de stap te kiezen die n zo laag mogelijk maakt en zo door te gaan, totdat het 1 bereikt. Het is echter duidelijk dat deze strategie hier niet werkt..
Als e = 10, zijn de stappen bijvoorbeeld: 10/2 = 5-1 = 4/2 = 2/2 = 1 (4 stappen). De optimale vorm is echter: 10-1 = 9/3 = 3/3 = 1 (3 stappen). Daarom moeten alle mogelijke stappen die kunnen worden uitgevoerd voor elke gevonden waarde van n worden geprobeerd, waarbij het minimumaantal van deze mogelijkheden wordt gekozen.
Alles begint met recursie: F (e) = 1 + min F (e-1), F (e / 2), F (e / 3) als e> 1, met als basisscenario: F (1) = 0. Met de herhalingsvergelijking kunnen we beginnen met het coderen van de recursie.
Het is echter duidelijk dat het overlappende subproblemen heeft. Bovendien hangt de optimale oplossing voor een bepaalde input af van de optimale oplossing van zijn deelproblemen.
Zoals bij onthouden, waar de oplossingen van de subproblemen die zijn opgelost, worden opgeslagen voor later gebruik. Of zoals bij dynamisch programmeren, begin je onderaan en werk je omhoog naar de gegeven e. Dan beide codes:
Een van de belangrijkste voordelen van het gebruik van dynamisch programmeren is dat het de verwerking versnelt, aangezien eerder berekende referenties worden gebruikt. Omdat het een recursieve programmeertechniek is, vermindert het de coderegels van het programma.
Hebzuchtige algoritmen lijken op dynamisch programmeren in die zin dat ze beide tools zijn voor optimalisatie. Het hebzuchtige algoritme zoekt echter bij elke lokale stap naar een optimale oplossing. Dat wil zeggen, het zoekt een hebzuchtige keuze in de hoop een wereldwijd optimum te vinden..
Daarom kunnen hebzuchtige algoritmen een aanname doen die er op dat moment optimaal uitziet, maar in de toekomst duur wordt en geen globaal optimum garandeert..
Anderzijds vindt dynamisch programmeren de optimale oplossing voor de deelproblemen en maakt vervolgens een weloverwogen keuze door de resultaten van die deelproblemen te combineren om daadwerkelijk de meest optimale oplossing te vinden..
- Er is veel geheugen nodig om het berekende resultaat van elk subprobleem op te slaan, waardoor niet kan worden gegarandeerd dat de opgeslagen waarde wordt gebruikt of niet.
- Vaak wordt de uitvoerwaarde opgeslagen zonder ooit te worden gebruikt in de volgende subproblemen tijdens de uitvoering. Dit leidt tot onnodig geheugengebruik.
- Bij dynamisch programmeren worden functies recursief aangeroepen. Hierdoor blijft het stapelgeheugen constant toenemen.
Als u een beperkt geheugen heeft om uw code uit te voeren en de verwerkingssnelheid geen probleem is, kunt u recursie gebruiken. Als u bijvoorbeeld een mobiele applicatie ontwikkelt, is het geheugen zeer beperkt om de applicatie uit te voeren.
Als u wilt dat het programma sneller werkt en u geen geheugenbeperkingen heeft, verdient het de voorkeur om dynamisch te programmeren.
Dynamisch programmeren is een effectieve methode om problemen op te lossen die anders buitengewoon moeilijk zouden lijken om binnen een redelijke tijd op te lossen..
Algoritmen op basis van het dynamische programmeerparadigma worden in veel wetenschapsgebieden gebruikt, waaronder veel voorbeelden in kunstmatige intelligentie, van het oplossen van problemen bij het plannen tot spraakherkenning..
Dynamisch programmeren is behoorlijk effectief en werkt erg goed voor een breed scala aan problemen. Veel algoritmen kunnen worden gezien als hebzuchtige algoritme-applicaties, zoals:
- Fibonacci-nummerreeks.
- Hanoi Torens.
- Alle kortste routeparen door Floyd-Warshall.
- Rugzakprobleem.
- Projectplanning.
- De kortste weg door Dijkstra.
- Vluchtcontrole en robotica controle.
- Wiskundige optimalisatieproblemen.
- Timesharing - Plan de taak om het CPU-gebruik te maximaliseren.
Fibonacci-nummers zijn de nummers die in de volgende volgorde worden gevonden: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, enz..
In wiskundige terminologie wordt de reeks Fn van Fibonacci-getallen gedefinieerd door de herhalingsformule: F (n) = F (n -1) + F (n -2), waarbij F (0) = 0 en F (1) = 1.
In dit voorbeeld wordt een zoekmatrix met alle beginwaarden geïnitialiseerd met -1. Wanneer de oplossing voor een deelprobleem nodig is, wordt eerst deze zoekmatrix doorzocht.
Als de berekende waarde aanwezig is, wordt die waarde geretourneerd. Anders wordt het resultaat berekend om in de zoekmatrix te worden opgeslagen, zodat het later opnieuw kan worden gebruikt.
In dit geval wordt voor dezelfde Fibonacci-reeks eerst f (0) berekend, daarna f (1), f (2), f (3), enzovoort. De oplossingen van de deelproblemen zullen dus van onderop worden geconstrueerd.
Niemand heeft nog op dit artikel gereageerd.