
Niet-lineaire programmeermethoden en oefeningen
De niet-lineaire programmering is het proces van het optimaliseren van een functie die afhankelijk is van verschillende onafhankelijke variabelen, die op hun beurt onderhevig zijn aan beperkingen.
Als een of meer van de beperkingen, of als de functie om te maximaliseren of te minimaliseren (aangeroepen Objectieve functie), wordt het niet uitgedrukt als een lineaire combinatie van de variabelen, dus we hebben een niet-lineair programmeerprobleem.
En daarom kunnen de procedures en methoden van lineair programmeren niet worden gebruikt.
De bekende methode kan bijvoorbeeld niet worden gebruikt Simplex, wat alleen van toepassing is als de doelfunctie en de beperkingen allemaal een lineaire combinatie zijn van de probleemvariabelen.
Artikel index
- 1 Methoden voor lineaire programmering
- 1.1 Voorbeeld van oplossing met grafische methode
- 2 oefeningen
- 2.1 - Oefening 1 (grafische methode)
- 2.2 - Oefening 2 (Analytische methode: Lagrange-vermenigvuldigers)
- 2.3 - Oefening 3 (nulgradiënt)
- 3 referenties
Lineaire programmeermethoden
Voor niet-lineaire programmeerproblemen zijn de belangrijkste te gebruiken methoden:
1. - Grafische methoden.
2.- Lagrange-multipliers om de grens van het oplossingsgebied te verkennen.
3.- Berekening van de gradiënt om extremen van de doelfunctie te onderzoeken.
4.- De methode van aflopende stappen om de null-verlooppunten te vinden.
5.- Gewijzigde methode van de Lagrange-vermenigvuldigers (met de Karush-Kuhn-Tucker-conditie).
Voorbeeld van oplossing met grafische methode
Een voorbeeld van een oplossing met de grafische methode is te zien in figuur 2:
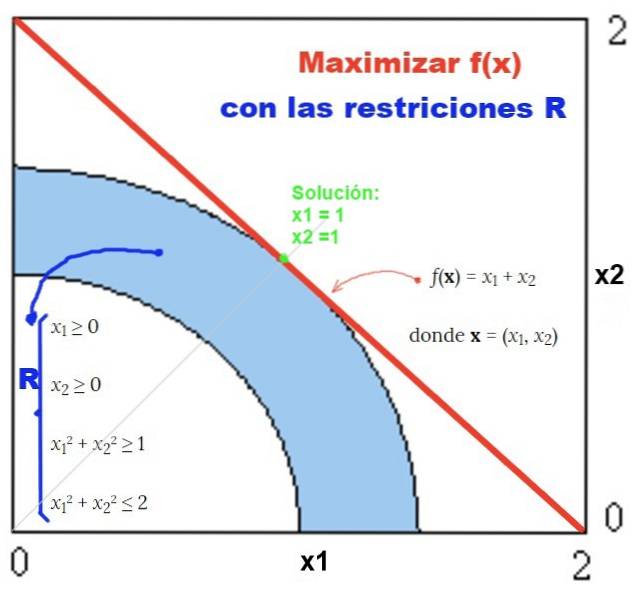
Opleiding
- Oefening 1 (grafische methode)
De winst G van een bepaald bedrijf is afhankelijk van de verkochte hoeveelheid van product X en de verkochte hoeveelheid van product Y, daarnaast wordt de winst bepaald door de volgende formule:
G = 2 (X - 2)twee + 3 (EN - 3)twee
Van de bedragen X en Y is bekend dat ze de volgende beperkingen hebben:
X≥0; Y≥0 en X + Y ≤ 7
Bepaal de waarden van X en Y die de maximale versterking produceren.
Oplossing
In dit probleem is de doelfunctie niet-lineair, terwijl de ongelijkheden die de beperkingen bepalen, dat wel zijn. Het is een probleem van niet-lineaire programmering.
Voor de oplossing van dit probleem wordt de grafische methode gekozen.
Eerst wordt het oplossingsgebied bepaald, dat wordt bepaald door de beperkingen.
Zoals X≥0; Y≥0, de oplossing moet gevonden worden in het eerste kwadrant van het XY-vlak, maar aangezien het ook zo moet zijn dat X + Y ≤ 7, zit de oplossing in het onderste halve vlak van de lijn X + Y = 7.
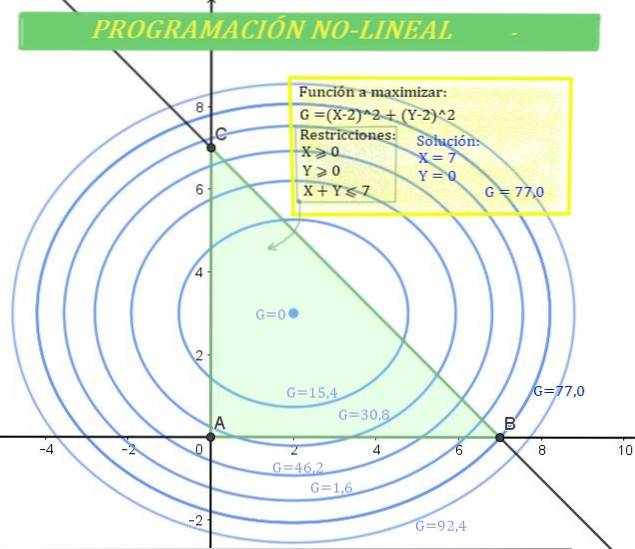
Het oplossingsgebied is het snijpunt van het eerste kwadrant met het onderste halve vlak van de lijn, waardoor een driehoekig gebied ontstaat waar de oplossing wordt gevonden. Het is hetzelfde als aangegeven in figuur 1.
Aan de andere kant kan de versterking G ook worden weergegeven in het cartesische vlak, aangezien de vergelijking die van een ellips is met middelpunt (2,3).
De ellips wordt weergegeven in figuur 1 voor verschillende waarden van G. Hoe hoger de waarde van G, hoe groter de versterking..
Er zijn oplossingen die tot de regio behoren, maar niet de maximale G-waarde geven, terwijl andere, zoals G = 92,4, buiten de groene zone liggen, dat wil zeggen de oplossingszone.
Dan komt de maximale waarde van G, zodat X en Y tot het oplossingsgebied behoren, overeen met:
G = 77 (maximale versterking), die wordt gegeven voor X = 7 en Y = 0.
Interessant is dat de maximale winst optreedt wanneer de verkoophoeveelheid van product Y nul is, terwijl de hoeveelheid product X de hoogst mogelijke waarde bereikt..
- Oefening 2 (Analytische methode: Lagrange-vermenigvuldigers)
Zoek de oplossing (x, y) die de functie f (x, y) = x maakttwee + 2 entwee maximaal zijn in de regio g (x, y) = xtwee + Ytwee - 1 = 0.
Oplossing
Het is duidelijk een niet-lineair programmeerprobleem, aangezien zowel de doelfunctie f (x, y) als de beperking g (x, y) = 0 geen lineaire combinatie zijn van de variabelen x en y.
De Lagrange-vermenigvuldigingsmethode zal worden gebruikt, waarvoor eerst de Lagrange-functie L (x, y, λ) moet worden gedefinieerd:
L (x, y, λ) = f (x, y) - λ g (x, y) = xtwee + 2 entwee - λ (xtwee + Ytwee - 1)
Waar λ een parameter is met de naam Lagrange-vermenigvuldiger.
Om de extreme waarden van de doelfunctie f te bepalen, in het oplossingsgebied gegeven door de beperking g (x, y) = 0, volgt u deze stappen:
-Vind de partiële afgeleiden van de Lagrange-functie L, met betrekking tot x, y, λ.
-Stel elke afgeleide in op nul.
Hier is de volgorde van deze bewerkingen:
- ∂L / ∂x = 2x - 2λx = 0
- ∂L / ∂y = 4y - 2λy = 0
- ∂L / ∂λ = - (xtwee + Ytwee - 1) = 0
Mogelijke systeemoplossingen
Een mogelijke oplossing van dit systeem is λ = 1 zodat aan de eerste vergelijking wordt voldaan, in welk geval y = 0 zodat aan de tweede wordt voldaan.
Deze oplossing houdt in dat x = 1 of x = -1 voor de derde vergelijking waaraan moet worden voldaan. Op deze manier zijn twee oplossingen S1 en S2 verkregen:
S1: (x = 1, y = 0)
S2: (x = -1, y = 0).
Het andere alternatief is dat λ = 2 zodat aan de tweede vergelijking wordt voldaan, ongeacht de waarde y.
In dit geval is de enige manier waarop aan de eerste vergelijking kan worden voldaan, dat x = 0. Gezien de derde vergelijking zijn er slechts twee mogelijke oplossingen, die we S3 en S4 zullen noemen:
S3: (x = 0, y = 1)
S4: (x = 0, y = -1)
Om erachter te komen welke of welke van deze oplossingen de doelfunctie maximaliseren, gaan we verder met het substitueren in f (x, y):
S1: f (1, 0) = 1twee + 2.0twee = 1
S2: f (-1, 0) = (-1)twee + 2.0twee = 1
S3: f (0, 1) = 0twee + 2.1twee = 2
S4: f (0, -1) = 0twee + eenentwintig)twee = 2
We concluderen dat de oplossingen die f maximaliseren, wanneer x en y tot de omtrek g (x, y) = 0 behoren, S3 en S4 zijn.
De paren waarden (x = 0, y = 1) en (x = 0, y = -1) maximaliseren f (x, y) in het oplossingsgebied g (x, y) = 0.
- Oefening 3 (nulgradiënt)
Vind oplossingen (x, y) voor de doelfunctie:
f (x, y) = xtwee + 2 entwee
Laat het maximum zijn in het gebied g (x, y) = xtwee + Ytwee - 1 ≤ 0.
Oplossing
Deze oefening is vergelijkbaar met oefening 2, maar het oplossings- (of beperkings) gebied strekt zich uit tot het binnengebied van de omtrek g (x, y) = 0, dat wil zeggen tot de cirkel g (x, y) ≤ 0. Dit omvat naar de omtrek en het binnenste gebied.
De oplossing aan de grens is al bepaald in opgave 2, maar het binnengebied moet nog worden verkend.
Om dit te doen, moet de gradiënt van de functie f (x, y) worden berekend en gelijk worden gesteld aan nul om extreme waarden in het oplossingsgebied te vinden. Dit komt overeen met het berekenen van de partiële afgeleiden van f met betrekking tot x en y respectievelijk en gelijk stellen aan nul:
∂f / ∂x = 2 x = 0
∂f / ∂y = 4 y = 0
Dit stelsel van vergelijkingen heeft als enige oplossing (x = 0, y = 0) die behoort tot de cirkel g (x, y) ≤ 0.
Het vervangen van deze waarde in de functie f resulteert in:
f (0, 0) = 0
Concluderend, de maximale waarde die de functie aanneemt in het oplossingsgebied is 2 en komt voor op de grens van het oplossingsgebied, voor de waarden (x = 0, y = 1) en (x = 0, y = -1 ).
Referenties
- Avriel, M. 2003. Niet-lineaire programmering. Dover Publishing.
- Bazaraa. 1979. Niet-lineaire programmering. John Wiley & Sons.
- Bertsekas, D. 1999. Niet-lineaire programmering: 2e editie. Athena Scientific.
- Nocedal, J. 1999. Numerieke optimalisatie. Springer-Verlag.
- Wikipedia. Niet-lineaire programmering. Hersteld van: es.wikipedia.com


Niemand heeft nog op dit artikel gereageerd.