
Verklaring van samengestelde proportionaliteit, samengestelde regel van drie, oefeningen
De samengestelde of meervoudige evenredigheid Het is de relatie tussen meer dan twee grootheden, waarbij directe en omgekeerde evenredigheid kan worden waargenomen tussen de gegevens en het onbekende. Dit is een meer geavanceerde versie van eenvoudige proportionaliteit, hoewel de technieken die in beide procedures worden gebruikt, vergelijkbaar zijn..
Als er bijvoorbeeld 7 mensen nodig zijn om 10 ton goederen in 3 uur te lossen, kan samengestelde proportionaliteit worden gebruikt om te berekenen hoeveel mensen er nodig zijn om 15 ton in 4 uur te lossen..
Om deze vraag te beantwoorden, is het handig om een tabel met waarden te maken om de grootheden en onbekenden te bestuderen en in verband te brengen.
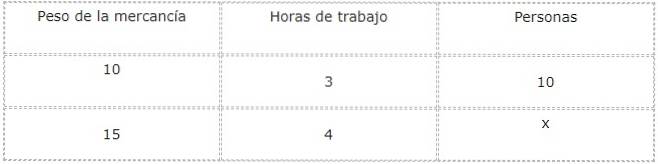
We gaan verder met het analyseren van de soorten relaties tussen elke omvang en het huidige onbekende, wat in dit geval overeenkomt met het aantal mensen dat zal werken.
Naarmate het gewicht van de koopwaar toeneemt, neemt ook het aantal mensen toe dat nodig is om deze uit te laden. Hierdoor is de relatie tussen gewicht en werknemers direct.
Aan de andere kant, naarmate het aantal werknemers toeneemt, nemen de werkuren af. Hierdoor is de relatie tussen mensen en werkuren van het omgekeerde type.
Artikel index
- 1 Hoe samengestelde proportionaliteiten te berekenen
- 2 Toelichting
- 3 Directe regel van drie
- 4 Inverse regel van drie
- 5 Conditie
- 6 Verificatie van resultaten
- 7 Opruiming
- 8 Geschiedenis
- 9 Opgeloste oefeningen
- 9.1 Oefening 1
- 9.2 Oefening 2
- 10 Voorgestelde oefeningen
- 11 Referenties
Hoe samengestelde proportionaliteiten te berekenen
Om voorbeelden zoals hierboven op te lossen, wordt meestal de samengestelde regel van drie methoden gebruikt. Dit bestaat uit het vaststellen van de soorten relaties tussen grootheden en onbekenden en vervolgens een product tussen breuken weergeven.
Met betrekking tot het eerste voorbeeld zijn de breuken die overeenkomen met de waardetabel als volgt georganiseerd:
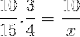
Maar voordat het onbekende wordt opgelost en opgelost, moeten de breuken die overeenkomen met de inverse relatie worden omgekeerd. Wat voor dit geval overeenkomt met de variabele tijd. Op deze manier is de op te lossen operatie:
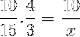
Wiens enige verschil de inversie is van de breuk die overeenkomt met de tijdvariabele 4/3. We gaan verder met werken en wissen de waarde van x.
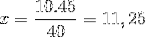
Er zijn dus meer dan elf mensen nodig om 15 ton goederen in 4 uur of minder te kunnen lossen.
Uitleg
Proportionaliteit is de constante relatie tussen grootheden die aan verandering onderhevig zijn, die symmetrisch zal zijn voor elk van de betrokken grootheden. Er zijn directe en omgekeerd evenredige relaties, waardoor de parameters van enkelvoudige of samengestelde proportionaliteit worden gedefinieerd.
Directe regel van drie
Het bestaat uit een proportionele relatie tussen variabelen, die hetzelfde gedrag vertonen wanneer ze worden gewijzigd. Het komt zeer vaak voor bij de berekening van percentages die verwijzen naar andere grootheden dan honderd, waarbij de fundamentele structuur ervan wordt gewaardeerd.
Als voorbeeld kan 15% worden berekend van 63. Op het eerste gezicht valt dit percentage niet gemakkelijk in te zien. Maar als je de regel van drie implementeert, kan de volgende relatie worden gelegd: als 100% 63 is, dan 15%, hoeveel zal dan zijn?
100% - 63
15% -X
En de bijbehorende bewerking is:
(15%. 63) / 100% = 9,45
Waar de procenttekens worden vereenvoudigd en het cijfer 9,45 wordt verkregen, wat overeenkomt met 15% van 63.
Inverse regel van drie
Zoals de naam aangeeft, is in dit geval de relatie tussen de variabelen het tegenovergestelde. De omgekeerde relatie moet worden vastgesteld voordat u verder gaat met de berekening. De procedure is homoloog aan die van de directe regel van drie, met uitzondering van de investering in de te berekenen breuk..
3 schilders hebben bijvoorbeeld 5 uur nodig om één muur af te werken. In hoeveel uur zouden 4 schilders het afmaken?
In dit geval is de relatie omgekeerd, aangezien naarmate het aantal schilders toeneemt, de werktijd zou moeten afnemen. De relatie is gelegd;
3 schilders - 5 uur
4 schilders - X uur
Als de relatie wordt omgekeerd, wordt de volgorde van bewerkingen omgekeerd. Dit is de juiste manier;
(3 schilders). (5 uur) / 4 schilders = 3,75 uur
De term schilders is vereenvoudigd en het resultaat is 3,75 uur.
Staat
Om in de aanwezigheid van een samengestelde of meervoudige proportionaliteit te zijn, is het noodzakelijk om beide soorten relaties tussen de grootheden en variabelen te vinden.
- Direct: de variabele heeft hetzelfde gedrag als de onbekende. Dat wil zeggen, wanneer de ene toeneemt of afneemt, verandert de andere evenredig.
- Inverse: de variabele vertoont een antoniem gedrag ten opzichte van dat van het onbekende. De breuk die de genoemde variabele in de waardetabel definieert, moet worden geïnverteerd om de omgekeerd evenredige relatie tussen variabele en onbekend weer te geven..
Verificatie van resultaten
Het is heel gebruikelijk om de volgorde van de groottes te verwarren bij het werken met samengestelde proportionaliteiten, in tegenstelling tot wat er gebeurt in de gebruikelijke verhoudingsberekeningen, waarvan de aard meestal direct en oplosbaar is door middel van een eenvoudige regel van drie..
Om deze reden is het belangrijk om de logische volgorde van de resultaten te onderzoeken en de samenhang te verifiëren van de cijfers die worden geproduceerd door de regel van drie samengestelde.
In het eerste voorbeeld zou het maken van een dergelijke fout resulteren in 20 als resultaat. Dat wil zeggen, 20 mensen lossen 15 ton koopwaar in 4 uur.
Op het eerste gezicht lijkt het geen gek resultaat, maar het is merkwaardig een toename van bijna 200% in personeel (van 7 naar 20 personen) wanneer de toename van koopwaar 50% is, en zelfs met een grotere tijdsmarge om voer het werk uit.
Op deze manier vormt de logische verificatie van de resultaten een belangrijke stap bij het implementeren van de regel van drie verbindingen..
Opruiming
Hoewel het meer basaal van aard is met betrekking tot wiskundige opleiding, vormt de goedkeuring een belangrijke stap in gevallen van proportionaliteit. Een verkeerde klaring is voldoende om elk resultaat verkregen met de eenvoudige of samengestelde regel van drie ongeldig te maken..
Verhaal
De regel van drie werd in het Westen bekend via de Arabieren, met publicaties van verschillende auteurs. Onder hen Al-Jwarizmi en Al-Biruni.
Al-Biruni had, dankzij zijn multiculturele kennis, toegang tot uitgebreide informatie over deze praktijk tijdens zijn reizen naar India, waarbij hij verantwoordelijk was voor de meest uitgebreide documentatie over de regel van drie.
Hij betoogt in zijn onderzoek dat India de eerste plaats was waar het gebruik van de regel van drie algemeen werd. De schrijver verzekert dat het op een vloeiende manier werd uitgevoerd in zijn directe, omgekeerde en zelfs samengestelde versies..
De exacte datum waarop de regel van drie onderdeel werd van de wiskundige kennis van India is nog onbekend. Het oudste document dat deze praktijk behandelt, het Bakhshali-manuscript, werd echter in 1881 ontdekt. Het bevindt zich momenteel in Oxford..
Veel wiskundehistorici beweren dat dit manuscript dateert uit het begin van het huidige tijdperk..
Opgeloste oefeningen
Oefening 1
Een luchtvaartmaatschappij moet 1.535 mensen vervoeren. Het is bekend dat het met 3 vliegtuigen 12 dagen zou duren om de laatste passagier op de bestemming te krijgen. 450 meer mensen zijn bij de luchtvaartmaatschappij aangekomen en 2 vliegtuigen moeten worden gerepareerd om bij deze taak te helpen. Hoeveel dagen heeft de luchtvaartmaatschappij nodig om de laatste passagier naar hun bestemming te vervoeren??
De relatie tussen het aantal mensen en het aantal werkdagen is direct, want hoe groter het aantal mensen, hoe meer dagen er nodig zijn om dit werk uit te voeren..
Aan de andere kant is de relatie tussen vliegtuigen en dagen omgekeerd evenredig. Naarmate het aantal vliegtuigen toeneemt, nemen de dagen die nodig zijn om alle passagiers over te brengen af.
De tabel met waarden die naar dit geval verwijst, is gemaakt.

Zoals gedetailleerd in het eerste voorbeeld, moeten de teller en de noemer worden omgekeerd in de breuk die overeenkomt met de inverse variabele ten opzichte van het onbekende. De werking is als volgt:
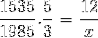
X = 71460/7675 = 9,31 dagen
Om 1985 mensen over te brengen met 5 vliegtuigen, duurt het meer dan 9 dagen.
Oefening 2
Een maïsoogst van 25 ton wordt naar de vrachtauto's gebracht. Het is bekend dat het hen vorig jaar 8 uur kostte met een loonlijst van 150 arbeiders. Als voor dit jaar de loonlijst met 35% is gestegen, hoe lang duurt het dan om de vrachtwagens te vullen met een oogst van 40 ton??
Voordat de waardetabel wordt weergegeven, moet het aantal werknemers voor dit jaar worden gedefinieerd. Dit is met 35% gestegen ten opzichte van het aanvankelijke aantal van 150 werknemers. Hiervoor wordt een directe regel van drie gebruikt.
100% - 150
35% - X
X = (35.100) / 100 = 52,5. Dit is het aantal extra werknemers ten opzichte van het voorgaande jaar, wat een totaal aantal werknemers van 203 oplevert, na afronding van het verkregen bedrag.
We gaan verder met het definiëren van de bijbehorende gegevenstabel

In dit geval vertegenwoordigt het gewicht een variabele die rechtstreeks verband houdt met de onbekende tijd. Aan de andere kant heeft de variabele workers een omgekeerde relatie met de tijd. Hoe groter het aantal werknemers, hoe korter de werkdag.
Rekening houdend met deze overwegingen en het omkeren van de breuk die overeenkomt met de arbeidersvariabele, gaan we verder met berekenen.
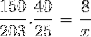
X = 40600/6000 = 6,76 uur
De dag duurt iets minder dan 7 uur.
Voorgestelde oefeningen
- Definieer 73% van 2875.
- Bereken het aantal uren dat Teresa slaapt, als bekend is dat ze maar 7% van het totaal van de dag slaapt. Bepaal hoeveel uur u per week slaapt.
- Een krant publiceert elke 5 uur 2000 exemplaren, met slechts 2 drukmachines. Hoeveel exemplaren produceert hij in 1 uur, als hij 7 machines gebruikt? Hoe lang duurt het om 10.000 kopieën te maken met 4 machines?
Referenties
- Encyclopedie Alvarez-initiatie. A. Álvarez, Antonio Álvarez Pérez. EDAF, 2001.
- Compleet basisinstructiehandboek voor basis- en hoger primair onderwijs: voor het gebruik van aspirant-leraren en in het bijzonder studenten van de normale scholen van de provincie, deel 1. Joaquín Avendaño. Druk van D. Dionisio Hidalgo, 1844.
- Rationele benadering van werkelijke functies. P. P. Petroesjev, Vasil Atanasov Popov. Cambridge University Press, 3 maart. 2011.
- Elementair rekenen voor lesgeven op scholen en hogescholen in Midden-Amerika. Darío González. Tip. Arenales, 1926.
- The Study of Mathematics: over de studie en moeilijkheden van wiskunde. Augustus De Morgan. Baldwin en Cradock, 1830.



Niemand heeft nog op dit artikel gereageerd.