De capacitieve reactantie is de weerstand die een condensator, een regulerend element van de ladingsstroom in een wisselstroomcircuit, zich verzet tegen het doorlaten van stroom.
In een circuit dat bestaat uit een condensator en wordt geactiveerd door een wisselstroombron, kan de capacitieve reactantie X worden gedefinieerdC als volgt:
XC = 1 / ωC
Of ook:
XC = 1 / 2πfC
Waarbij C de capaciteit van de condensator is en ω de hoekfrequentie van de bron, gerelateerd aan de frequentie f door:
ω = 2πf
Capacitieve reactantie hangt af van het omgekeerde van de frequentie, daarom is het bij hoge frequenties meestal klein, terwijl bij lage frequenties de reactantie groot is.
De internationale systeemeenheid voor het meten van capacitieve reactantie is de ohm (Ω), op voorwaarde dat de capaciteit C van de condensator in farad is (afgekort F) en de frequentie wordt uitgedrukt in inverse seconden (s-1.
Zolang de lading duurt, wordt een wisselspanning en -stroom tot stand gebracht via de condensator, waarvan de amplitudes of maximale waarden respectievelijk worden aangeduid als VC en ikC, zijn gerelateerd door capacitieve reactantie analoog aan de wet van Ohm:
V.C = IkC ⋅ XC
In een condensator is de spanning 90º achter de stroom, of de stroom is 90º voor op de stroom, zoals u verkiest. De frequentie is in ieder geval hetzelfde.
Toen XC is erg groot, de stroom neigt klein te zijn en de waarde van X neigt naar oneindigC, de condensator gedraagt zich als een open circuit en de stroom is nul.
Artikel index
Laten we een voorbeeld bekijken van het berekenen van capacitieve reactantie: stel dat een condensator van 6 μF is aangesloten op een stopcontact van 40 V en frequentie F. 60 Hz.
Om de capacitieve reactantie te vinden, wordt de aan het begin gegeven definitie gebruikt. De hoekfrequentie ω wordt gegeven door:
ω = 2πf = 2π x 60 Hz = 377 s-1
Vervolgens wordt dit resultaat vervangen in de definitie:
XC = 1 / ωC = 1 / (377 s-1x 6 x10 -6 F) = 442,1 ohm
Laten we nu eens kijken naar de amplitude van de stroom die in het circuit vloeit. Omdat de bron een spanning van amplitude V biedtC = 40 V, gebruiken we de relatie tussen capacitieve reactantie, stroom en spanning om de amplitude van de stroom of maximale stroom te berekenen:
ikC = VC / XC = 40 V / 442,1 ohm = 0,09047 A = 90,5 m A.
Als de frequentie erg groot wordt, wordt de capacitieve reactantie klein, maar als de frequentie 0 wordt en we een gelijkstroom hebben, is de reactantie meestal oneindig..
Wanneer een condensator is aangesloten op een wisselstroombron, terwijl deze oscilleert en van polariteit verandert, ervaart de condensator afwisselende ladingen en ontladingen..
Voor een frequentie van 60 Hz zoals in het voorbeeld, is de spanning 60 keer per seconde positief en nog eens 60 keer per seconde negatief.
Door de spanning te verhogen, wordt de stroom in één richting geduwd, maar als de condensator ontlaadt, wordt stroom geproduceerd in de tegenovergestelde richting die tegenover de eerste staat..
Als vC (t) = Vm sin ωt, wetende dat de capaciteit de verhouding is tussen de belasting en de spanning, zullen we de belasting hebben:
C = q / V → q (t) = CV = CVm sen ωt
En door de belasting als een functie van de tijd te hebben, hebben we de stroom, die daarvan de afgeleide is:
ikC(t) = CVm ω cos ωt
Maar de sinus en cosinus zijn gerelateerd door: cos α = sin (α + π / 2), dus:
ikC(t) = CVm ω zonde (ωt + π / 2) = ikC zonde (ωt + π / 2)
Met ikC = CVC ω
Zoals u kunt zien, is er een verschil van 90 ° van de voortgang van de stroom met betrekking tot de spanning, zoals in het begin werd opgemerkt.
In de beschrijving van dit type schakelingen wordt het concept van phasor, die sterk lijkt op een vector en waarmee elke wisselende hoeveelheid zoals stroom, spanning of impedantie in het complexe vlak kan worden weergegeven.
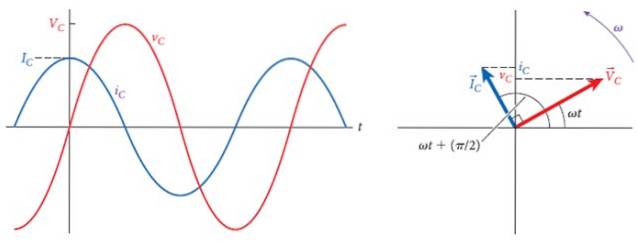
De volgende afbeelding toont, aan de rechterkant, de spanning- en stroomfasoren in de condensator, die een hoek van 90º tussen hen vormen, het faseverschil tussen de twee..
Aan de linkerkant zijn de respectievelijke grafieken, met verschillende amplitudes, maar dezelfde frequentie. Na verloop van tijd leidt de stroom de spanning en wanneer deze maximaal is, is de stroom nul en wanneer de spanning nul is, is de stroom maximaal, maar met omgekeerde polariteit.
In een circuit met weerstanden, condensatoren en inductanties is de reactantie het denkbeeldige deel van de impedantie Z, een complexe grootheid die in wisselstroomcircuits een vergelijkbare rol heeft als die van elektrische weerstand voor gelijkstroomcircuits..
In feite wordt de impedantie van een circuit gedefinieerd als de verhouding tussen spanning en stroom:
Z = V / I
Voor een condensator of condensator wordt de impedantie ervan gegeven door het quotiënt:
ZC = v (t) / ik (t) = VC zonde ωt / IC zonde (ωt + π / 2)
Een manier om spanning en stroom als fasoren uit te drukken, is door de amplitude en fasehoek (polaire vorm) aan te geven:
v (t) = VC ∠ 0º
ik (t) = ikC ∠ 90º
Daarom:
ZC = VC ∠ 0º / IC ∠ 90º = (VC / IkC) ∠ 0º -90º =
= VC / CVC ω ∠ -90º = (1 / ωC) ∠ -90º =
ZC = (- j) XC
Dat wil zeggen, de impedantie van de condensator is zijn capacitieve reactantie vermenigvuldigd met het negatief van de denkbeeldige eenheid.
De impedantie van een wisselstroomcircuit met weerstanden, condensatoren en inductoren kan ook binomiaal worden weergegeven door:
Z = R + jX
In deze vergelijking vertegenwoordigt R de weerstand, die overeenkomt met het reële deel, j is de imaginaire eenheid en X is de reactantie, die capacitief of inductief kan zijn of een combinatie van beide, als deze elementen tegelijkertijd aanwezig zijn in de circuit.
Als het circuit een weerstand en een condensator in serie bevat, is hun impedantie:
Z = ZR + ZC
Omdat bij weerstand de spanning en stroom in fase zijn, is de weerstandsimpedantie eenvoudigweg de waarde van de weerstand R.
In het geval van capacitieve impedantie hebben we al gezien dat ZC = -jXC , daarom is de impedantie van het RC-circuit:
Z = R - jXC = R - j (1 / ωC)
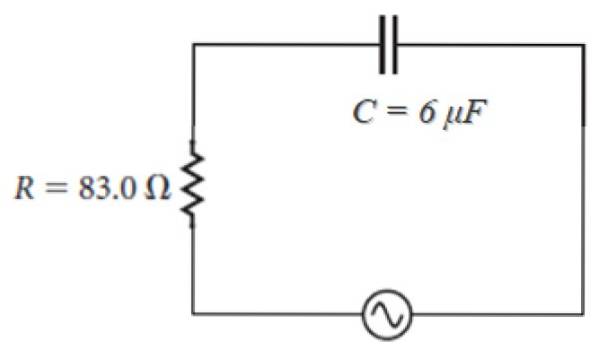
Bijvoorbeeld in het onderstaande circuit, waarvan de bron de vorm heeft:
100 V ⋅ zonde (120πt)
Als we zien dat ω = 120π, is de impedantie:
Z = 83,0 - j [(1 / (120π ⋅ 6 x 10-6)] ohm = 83,0 - 442,1 j ohm.
Hoogdoorlaatfilters, laagdoorlaatfilters, brugcircuits voor het meten van capaciteiten en inductanties en faseverschuivingscircuits behoren tot de belangrijkste toepassingen van circuits die capacitieve reactanties bevatten, in combinatie met inductanties en elektrische weerstanden..
Bij stereo's worden sommige luidsprekers geleverd met aparte luidsprekers. woofer (groter) voor lage frequenties en tweeter of kleine hoorn voor hoge frequenties. Dit verbetert de prestaties en audiokwaliteit.
Ze gebruiken condensatoren die de aankomst van lage frequenties in de tweeter voorkomen, terwijl in de woofer een inductor wordt toegevoegd om hoogfrequente signalen te vermijden, aangezien de inductantie een reactantie heeft die evenredig is met de frequentie: XL. = 2πfL.
Niemand heeft nog op dit artikel gereageerd.