
Bravais netwerken concept, kenmerken, voorbeelden, oefeningen
De Bravais-netten Ze zijn de set van veertien driedimensionale eenheidscellen waarin de atomen van een kristal kunnen worden gelokaliseerd. Deze cellen bestaan uit een driedimensionale rangschikking van punten die een basisstructuur vormen die periodiek wordt herhaald in de drie ruimtelijke richtingen..
De oorsprong van deze benaming voor de kristallijne basisstructuren komt uit 1850, toen Auguste Bravais aantoonde dat er slechts 14 mogelijke driedimensionale basiseenheidscellen zijn..

De set van 14 Bravais-netwerken is onderverdeeld in zeven groepen of structuren volgens de geometrie van de cellen, deze zeven groepen zijn:
1- Kubiek
2- Tetragonal
3- Orthorhombisch
4- Trigonaal-zeshoekig
5- Monokliniek
6- Trikliniek
7- Trigonal
Elk van deze structuren definieert een eenheidscel, dit is het kleinste deel dat de geometrische rangschikking van de atomen in het kristal behoudt..
Artikel index
- 1 Kenmerken van Bravais-netwerken
- 1.1 Kubieke netwerken
- 2 voorbeelden
- 2.1 - IJzer
- 2.2 - Koper
- 2.3 - Kostbare edelstenen
- 2.4 Topaas
- 3 Opgeloste oefeningen
- 3.1 Oefening 1
- 3.2 Oefening 2
- 3.3 Oefening 3
- 4 referenties
Kenmerken van Bravais-netwerken
De veertien Bravais-netwerken zijn, zoals hierboven vermeld, onderverdeeld in zeven groepen. Maar elk van deze groepen heeft zijn eenheidscellen met zijn karakteristieke parameters die zijn:
1- De netwerkparameter (a, b, c)
2- Aantal atomen per cel
3- Verband tussen netwerkparameter en atoomradius
4- Coördinatienummer
5- Verpakkingsfactor
6- interstitiële spaties
7- Door translaties langs de vectoren a, b, c wordt de kristalstructuur herhaald.
Kubieke netwerken
Het bestaat uit het eenvoudige kubieke of kubieke netwerk P, face-centered cubic network of cubic network F en het body-centered cubic network of cubic network I.
Alle kubieke netwerken hebben alle drie netwerkparameters overeenkomend met de x-, y-, z-richtingen met dezelfde waarde:
a = b = c
Kubisch netwerk P
Opgemerkt moet worden dat atomen worden weergegeven door bollen waarvan het middelpunt zich op de hoekpunten van de kubieke eenheidscel P bevindt.
In het geval van het kubische rooster P de aantal atomen per cel is 1, omdat bij elk hoekpunt slechts een achtste van het atoom zich in de eenheidscel bevindt, dus 8 * ⅛ = 1.
De coördinatiegetal geeft het aantal atomen aan dat naaste buren in het kristalrooster is. In het geval van het kubische rooster P is het coördinatiegetal 6.
Kubisch netwerk I
In dit type netwerk bevindt zich naast de atomen op de hoekpunten van de kubus, een atoom in het midden van de kubus. Dus de aantal atomen per cel eenheid in kubisch rooster P is 2 atomen.

Kubisch netwerk F
Het is het kubische rooster dat, naast de atomen in de hoekpunten, een atoom heeft in het midden van het vlak van elke kubus. De aantal atomen per cel is 4, aangezien elk van de zes atomen van het vlak de helft in de cel heeft, dat wil zeggen 6 * ½ = 3 plus 8 * ⅛ = 1 bij de hoekpunten.

Zeshoekig net
In dit geval is de eenheidscel een recht prisma met een zeshoekige basis. Zeshoekige netwerken hebben alle drie netwerkparameters corresponderend het vervullen van de volgende relatie:
een = b ≠ c
De hoek tussen vector a en b is 120º, zoals weergegeven in de figuur. Terwijl tussen vectoren a en c, evenals tussen b en c, rechte hoeken worden gevormd.

De aantal atomen per cel wordt als volgt berekend:
- In elk van de 2 bases van het hexagonale prisma bevinden zich 6 atomen op de zes hoekpunten. Elk van deze atomen bezet ⅙ van de eenheidscel.
- In het midden van elk van de 2 hexagonale basen bevindt zich 1 atoom dat een 1/2 eenheidscel inneemt.
- Op de 6 zijvlakken van het hexagonale prisma bevinden zich 3 atomen die elk ⅔ van de eenheidscel bezetten en 3 atomen die elk ⅓ van het eenheidscelvolume bezetten..
(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6
De relatie tussen de roosterparameters a en b met de atoomstraal R onder de aanname dat alle atomen een gelijke straal hebben en in contact zijn, is:
a / R = b / R = 2
Voorbeelden
Metalen zijn de belangrijkste voorbeelden van kristallijne structuren en ook de eenvoudigste omdat ze over het algemeen uit slechts één type atoom bestaan. Maar er zijn andere niet-metallische verbindingen die ook kristallijne structuren vormen, zoals diamant, kwarts en vele andere..
- Het ijzer
IJzer heeft een enkele kubieke eenheidscel met rooster- of randparameter a = 0,297 nm. In 1 mm zijn er 3,48 x 10 ^ 6 eenheidscellen.
- Koper
Het heeft een kubische kristallijne structuur met het gezicht in het midden, die uitsluitend uit koperatomen bestaat..
- Kostbare edelstenen
Kostbare edelstenen zijn kristallijne structuren van in wezen dezelfde samenstelling, maar met kleine porties onzuiverheden die vaak verantwoordelijk zijn voor hun kleur..
Diamant
Het is uitsluitend samengesteld uit koolstof en bevat geen onzuiverheden, daarom is het kleurloos. De diamant heeft kubieke kristalstructuur (isometrisch-hexoctaëdrisch) en is het moeilijkste bekende materiaal.
Kwarts
Het is samengesteld uit siliciumoxide, het is over het algemeen kleurloos of wit. De kristallijne structuur is trigonaal-trapezohedraal.
Robijn
Het is samengesteld uit aluminiumoxide met chroomverontreinigingen die het zijn karakteristieke rode kleur geven. Vorm een zeshoekig kristalrooster.
Saffier
Het is ook een kristal van aluminiumoxide, maar met onzuiverheden van titanium en ijzer, die verantwoordelijk zijn voor de blauwe kleur in verschillende tinten. Zoals de robijn heeft zeshoekige structuur.
Jade
Edelsteen is over het algemeen groen van kleur, heeft monokliene structuur en is samengesteld uit ijzer-magnesium-calciumsilicaat.
Topaas
Het is kleurloos met een orthorhombische structuur aluminiumfluoride-hydroxide-silicaat.
Opgeloste oefeningen
Oefening 1
Zoek de relatie tussen de roosterparameter en de atoomstraal voor een kubisch rooster F.
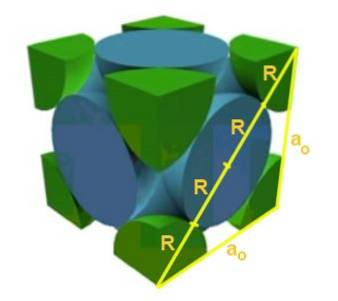
Oplossing: Ten eerste wordt aangenomen dat de atomen worden weergegeven als bollen met alle straal R die in "contact" met elkaar staan, zoals weergegeven in de figuur. Er ontstaat een rechthoekige driehoek waarin het waar is dat:
(4 R) ^ 2 = a ^ 2 + a ^ 2 = 2 a ^ 2
Daarom is de relatie tussen rand en straal:
a / R = 4 / √2
Oefening 2
Zoek de relatie tussen de roosterparameter en de atoomstraal voor een kubisch rooster I (lichaamsgericht).
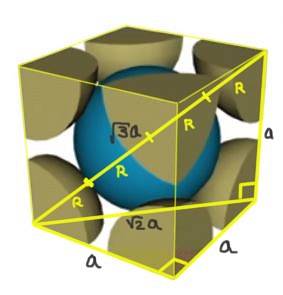
Oplossing: Atomen worden verondersteld te worden weergegeven als bollen met alle straal R in "contact" met elkaar, zoals weergegeven in de afbeelding.
Er worden twee rechthoekige driehoeken gevormd, een met hypotenusa √2a en de andere met hypotenusa √3a, zoals kan worden aangetoond met de stelling van Pythagoras. Van daaruit volgt dat de relatie tussen de roosterparameter en de atoomstraal voor een kubisch rooster I (gecentreerd in het lichaam) is:
a / R = 4 / √3
Oefening 3
Zoek de pakkingsfactor F voor een eenheidscel met een kubische structuur F (vlakgecentreerd kubiek) waarin de atomen een straal R hebben en in "contact" staan.
Oplossing: De pakkingsfactor F wordt gedefinieerd als het quotiënt tussen het volume dat wordt ingenomen door de atomen in de eenheidscel en het volume van de cel:
F = Vatomen / Vcel
Zoals hierboven aangetoond, is het aantal atomen per eenheidscel in een kubisch rooster met het midden van het oppervlak 4, dus de pakkingsfactor is:
F = 4 [4πR ^ 3/3] / [a ^ 3] =…
… 4 [4πR ^ 3/3] / [4R / √2] ^ 3 = (√2) π / 6 = 0,74
Referenties
- Crystal Structures Academic Resource Center. [Pdf]. Opgehaald op 24 mei 2018, van: web.iit.edu
- Kristallen. Opgehaald op 26 mei 2018, van: thoughtco.com
- Persboeken. 10.6 Roosterstructuren in kristallijne vaste stoffen. Opgehaald op 26 mei 2018, van: opentextbc.ca
- Ming. (2015, 30 juni). Typen kristalstructuren. Opgehaald op 26 mei 2018, van: crystalvisions-film.com
- Helmenstine, Anne Marie, Ph.D. (31 januari 2018). Types van
- Kittel Charles (2013) Solid State Physics, Condensed matter Physics (8e editie). Wiley.
- KHI. (2007). Kristallijne structuren. Opgehaald op 26 mei 2018, van: folk.ntnu.no
- Wikipedia. Bravais-roosters. Hersteld van: en.wikipedia.com.



Niemand heeft nog op dit artikel gereageerd.