
Breking van lichtelementen, wetten en experiment

De lichtbreking Het is het optische fenomeen dat optreedt wanneer licht schuin valt op het scheidingsoppervlak van twee media met een verschillende brekingsindex. Wanneer dit gebeurt, verandert het licht van richting en snelheid.
Breking treedt bijvoorbeeld op wanneer licht van lucht naar water gaat, omdat dit een lagere brekingsindex heeft. Het is een fenomeen dat perfect kan worden waargenomen in het zwembad, wanneer men observeert hoe de vormen van het lichaam onder water lijken af te wijken van de richting die ze zouden moeten hebben..

Het is een fenomeen dat verschillende soorten golven beïnvloedt, hoewel het geval van licht het meest representatief is en het meest aanwezig in ons dagelijks leven..
De verklaring voor de breking van licht werd gegeven door de Nederlandse natuurkundige Willebrord Snell van Royen, die een wet heeft opgesteld om het uit te leggen die bekend is geworden als de Wet van Snell..
Een andere wetenschapper die speciale aandacht besteedde aan de breking van licht, was Isaac Newton. Om het te bestuderen, creëerde hij het beroemde glazen prisma. In het prisma dringt licht het door een van zijn gezichten, brekend en ontbindend in de verschillende kleuren. Op deze manier bewees hij door het fenomeen van lichtbreking dat wit licht is samengesteld uit alle kleuren van de regenboog..
Artikel index
- 1 Elementen van breking
- 1.1 Brekingsindex van licht in verschillende media
- 2 Brekingswetten
- 2.1 Eerste wet van breking
- 2.2 Tweede wet van breking
- 2.3 Het principe van Fermat
- 2.4 Gevolgen van de wet van Snell
- 2.5 Grenshoek en totale interne reflectie
- 3 experimenten
- 3.1 Oorzaken
- 4 De breking van licht in het dagelijks leven
- 5 referenties
Elementen van breking
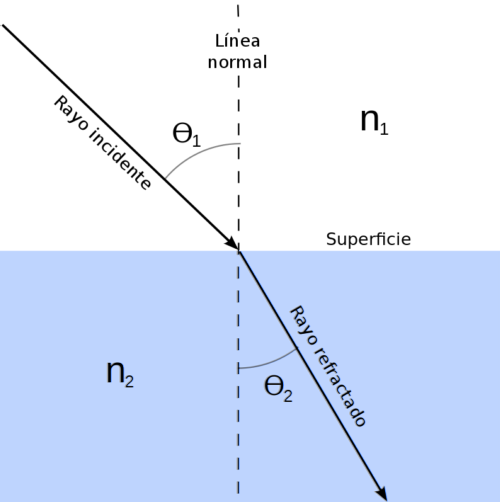
De belangrijkste elementen waarmee rekening moet worden gehouden bij de studie van de breking van licht zijn de volgende: -De invallende straal, de straal die schuin op het scheidingsoppervlak van de twee fysieke media valt. -De gebroken straal, de straal die door het medium gaat en zijn richting en snelheid wijzigt. -De normale lijn, de denkbeeldige lijn loodrecht op het scheidingsoppervlak van de twee media. -De invalshoek (i), die wordt gedefinieerd als de hoek gevormd door de invallende straal met de normaal. -De brekingshoek (r), die wordt gedefinieerd als de hoek gevormd door de normaal met de gebroken straal.-Daarnaast moet ook rekening worden gehouden met de brekingsindex (n) van een medium, dat is het quotiënt van de lichtsnelheid in vacuüm en de lichtsnelheid in het medium..
n = c / v
In dit verband moet eraan worden herinnerd dat de lichtsnelheid in vacuüm de waarde aanneemt van 300.000.000 m / s.
Brekingsindex van licht in verschillende media
De brekingsindices van licht in enkele van de meest voorkomende media zijn:
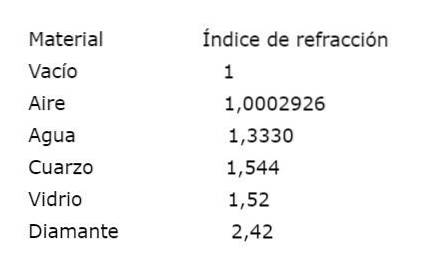
Wetten van breking
De wet van Snell wordt vaak de wet van breking genoemd, maar de waarheid is dat kan worden gezegd dat de wetten van breking twee zijn.
Eerste wet van breking
De invallende straal, de gebroken straal en de normaal bevinden zich in hetzelfde vlak van ruimte. In deze wet, ook afgeleid door Snell, is de reflectie ook van toepassing.
Tweede wet van breking
De tweede, de brekingswet of de wet van Snell, wordt bepaald door de volgende uitdrukking:
n1 zonde i = ntwee sen r
Zijn n1 de brekingsindex van het medium waaruit het licht komt; i de invalshoek; ntwee de brekingsindex van het medium waarin het licht wordt gebroken; r de brekingshoek.
Het principe van Fermat
Uit het principe van minimumtijd of het principe van Fermat kunnen zowel de wetten van reflectie als de wetten van breking worden afgeleid, die we zojuist hebben gezien.
Dit principe bevestigt dat het echte pad dat wordt gevolgd door een lichtstraal die tussen twee punten in de ruimte beweegt, het pad is dat de minste tijd nodig heeft om te reizen..
Gevolgen van de wet van Snell
Enkele van de directe gevolgen die worden afgeleid uit de vorige uitdrukking zijn:
a) Als ntwee > n1 sen r < sen i o sea r < i
Dus wanneer een lichtstraal van een medium met een lagere brekingsindex naar een ander met een hogere brekingsindex gaat, nadert de gebroken straal de normale.
b) Als n2 < n1 sin r> sin i of r> i
Dus wanneer een lichtstraal van een medium met een hogere brekingsindex naar een ander met een lagere index gaat, beweegt de gebroken straal weg van de normale.
c) Als de invalshoek nul is, dan is de hoek van de brekingsstraal ook nul.
Grenshoek en totale interne reflectie
Een ander belangrijk gevolg van de wet van Snell is wat bekend staat als de beperkende hoek. Dit is de naam die wordt gegeven aan de invalshoek die overeenkomt met een brekingshoek van 90º.
Wanneer dit gebeurt, beweegt de gebroken straal gelijk met het scheidingsoppervlak van de twee media. Deze hoek wordt ook wel de kritische hoek genoemd.
Voor hoeken die groter zijn dan de limiethoek, treedt het fenomeen totale interne reflectie op. Wanneer dit gebeurt, treedt er geen breking op, aangezien de gehele lichtbundel intern wordt gereflecteerd. Totale interne reflectie vindt alleen plaats bij de overgang van een medium met een hogere brekingsindex naar een medium met een lagere brekingsindex.
Een toepassing van totale interne reflectie is de geleiding van licht door de optische vezel zonder energieverlies. Dankzij dit kunnen we genieten van de hoge gegevensoverdrachtsnelheden die worden geboden door glasvezelnetwerken.
Experimenten
Een heel basaal experiment om het fenomeen refractie te kunnen waarnemen, bestaat uit het inbrengen van een potlood of een pen in een glas vol water. Als gevolg van de breking van licht lijkt het ondergedompelde deel van het potlood of de pen enigszins gebroken of afwijkend van het pad dat men zou verwachten..

U kunt ook een soortgelijk experiment proberen met een laserpointer. Het is natuurlijk nodig om een paar druppels melk in het glas water te gieten om de zichtbaarheid van het laserlicht te verbeteren. In dit geval wordt aanbevolen dat het experiment wordt uitgevoerd bij weinig licht om het pad van de lichtstraal beter te kunnen waarderen..
In beide gevallen is het interessant om verschillende invalshoeken te proberen en te observeren hoe de brekingshoek varieert naarmate ze veranderen..
Oorzaken
De oorzaken van dit optische effect moeten worden gevonden in de breking van licht waardoor het beeld van het potlood (of de lichtstraal van de laser) onder water afwijkt van het beeld dat we in de lucht zien..
De breking van licht in het dagelijks leven
De breking van licht kan in veel situaties van onze dag worden waargenomen. Sommige hebben we al genoemd, andere zullen we hieronder bespreken.
Een gevolg van breking is dat poelen ondieper lijken te zijn dan ze in werkelijkheid zijn..
Een ander effect van breking is de regenboog die ontstaat doordat licht wordt gebroken door de waterdruppels die in de atmosfeer aanwezig zijn. Het is hetzelfde fenomeen dat optreedt wanneer een lichtstraal door een prisma gaat.
Een ander gevolg van de breking van licht is dat we de zonsondergang van de zon waarnemen als er enkele minuten zijn verstreken sinds het feitelijk heeft plaatsgevonden..
Referenties
- Licht (n.d.). Op Wikipedia. Opgehaald op 14 maart 2019, via en.wikipedia.org.
- Burke, John Robert (1999). Fysica: de aard van de dingen. Mexico DF: International Thomson Editores.
- Totale interne reflectie (n.d.). Op Wikipedia. Opgehaald op 12 maart 2019, via en.wikipedia.org.
- Licht (n.d.). Op Wikipedia. Opgehaald op 13 maart 2019, via en.wikipedia.org.
- Lekner, John (1987). Theory of Reflection, of Electromagnetic and Particle Waves. Springer.
- Breking (n.d.). Op Wikipedia. Opgehaald op 14 maart 2019, via en.wikipedia.org.
- Crawford jr., Frank S. (1968). Golven (Berkeley Physics Course, Vol.3), McGraw-Hill.



Niemand heeft nog op dit artikel gereageerd.