
Sturges Regel Uitleg, Toepassingen en Voorbeelden
De sturges heersen het is een criterium dat wordt gebruikt om het aantal klassen of intervallen te bepalen dat nodig is om een reeks statistische gegevens grafisch weer te geven. Deze regel werd in 1926 uitgesproken door de Duitse wiskundige Herbert Sturges.
Sturges stelde een eenvoudige methode voor, gebaseerd op het aantal steekproeven x waarmee we het aantal klassen en hun bereikbreedte konden vinden. De regel van Sturges wordt veel gebruikt, vooral op het gebied van statistiek, in het bijzonder om frequentiehistogrammen te construeren..
Artikel index
- 1 Toelichting
- 2 Toepassingen
- 3 Voorbeeld
- 4 referenties
Uitleg
De regel van Sturges is een empirische methode die veel wordt gebruikt in beschrijvende statistieken om het aantal klassen te bepalen dat in een frequentiehistogram moet bestaan, om een set gegevens te classificeren die een steekproef of populatie vertegenwoordigen..
In wezen bepaalt deze regel de breedte van de grafische containers, van de frequentiehistogrammen.
Om zijn regel vast te stellen beschouwde Herbert Sturges een ideaal frequentiediagram, bestaande uit K-intervallen, waarbij het i-de interval een bepaald aantal samples bevat (i = 0, ... k - 1), weergegeven als:
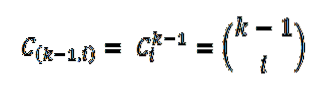
Dat aantal samples wordt bepaald door het aantal manieren waarop een subset van een set kan worden geëxtraheerd; dat wil zeggen door de binominale coëfficiënt, uitgedrukt als volgt:
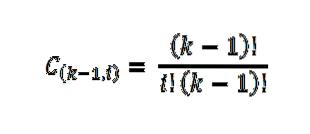
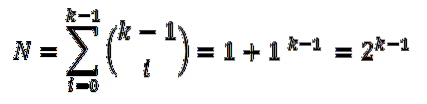
Om de uitdrukking te vereenvoudigen, paste hij de eigenschappen van logaritmen toe op beide delen van de vergelijking:
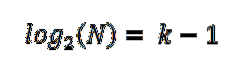
Zo stelde Sturges vast dat het optimale aantal intervallen k wordt gegeven door de uitdrukking:
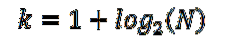
Het kan ook worden uitgedrukt als:

In deze uitdrukking:
- k is het aantal klassen.
- N is het totale aantal waarnemingen in de steekproef.
- Log is de algemene logaritme van grondtal 10.
Om bijvoorbeeld een frequentiehistogram te maken dat een willekeurige steekproef van de lengte van 142 kinderen uitdrukt, is het aantal intervallen of klassen dat de verdeling zal hebben:
k = 1 + 3.322 logboek10 (N)
k = 1 + 3.322 logboek (142)
k = 1 + 3.322 2.1523
k = 8,14 ≈ 8
De verdeling is dus in 8 intervallen.
Het aantal intervallen moet altijd worden weergegeven door hele getallen. In gevallen waarin de waarde een decimaal getal is, moet een benadering worden gemaakt naar het dichtstbijzijnde gehele getal.
Toepassingen
De regel van Sturges wordt voornamelijk toegepast in de statistiek, omdat hiermee een frequentieverdeling kan worden gemaakt door het aantal klassen (k) te berekenen, evenals de lengte van elk van deze, ook wel amplitude genoemd..
De amplitude is het verschil tussen de boven- en ondergrens van de klasse, gedeeld door het aantal klassen, en wordt uitgedrukt:
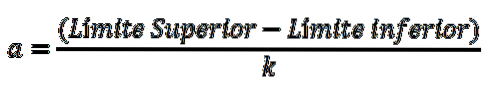
Er zijn veel vuistregels waarmee je een frequentieverdeling kunt maken. De regel van Sturges wordt echter vaak gebruikt omdat deze het aantal klassen benadert, dat over het algemeen varieert van 5 tot 15..
Het beschouwt dus een waarde die een steekproef of populatie adequaat vertegenwoordigt; dat wil zeggen, de benadering vertegenwoordigt geen extreme groeperingen, noch werkt het met een buitensporig aantal klassen waardoor de steekproef niet kan worden samengevat..
Voorbeeld
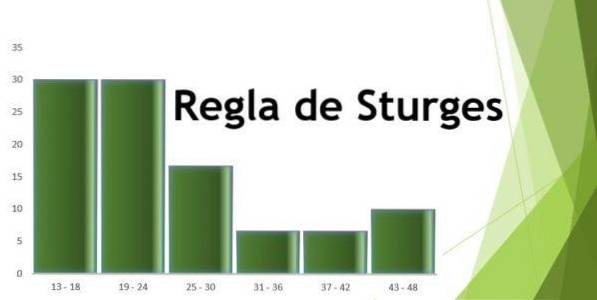
Er moet een frequentiehistogram worden gemaakt op basis van de gegeven gegevens, die overeenkomen met de leeftijden die zijn verkregen in een onderzoek onder mannen die trainen in een plaatselijke sportschool..

Om de intervallen te bepalen, moet men de grootte van de steekproef of het aantal waarnemingen kennen; in dit geval heb je 30.
Dan is de Sturges-regel van toepassing:
k = 1 + 3.322 logboek10 (N)
k = 1 + 3.322 logboek (30)
k = 1 + 3.322 1.4771
k = 5,90 ≈ 6 intervallen.
Uit het aantal intervallen kan de amplitude worden berekend die deze zullen hebben; dat wil zeggen, de breedte van elke staaf weergegeven in het frequentiehistogram:
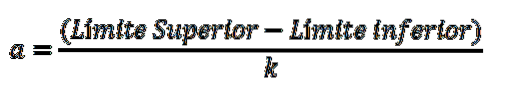
De ondergrens wordt als de kleinste waarde van de gegevens beschouwd en de bovengrens is de grootste waarde. Het verschil tussen de boven- en ondergrens wordt het bereik of bereik van de variabele (R) genoemd.
Uit de tabel blijkt dat de bovengrens 46 is en de ondergrens 13; op die manier zal de amplitude van elke klas zijn:
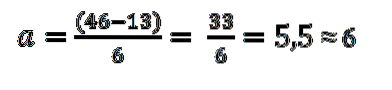
De intervallen bestaan uit een boven- en ondergrens. Om deze intervallen te bepalen, beginnen we met te tellen vanaf de ondergrens, waarbij we de amplitude die bepaald wordt door regel (6) hieraan toevoegen, als volgt:
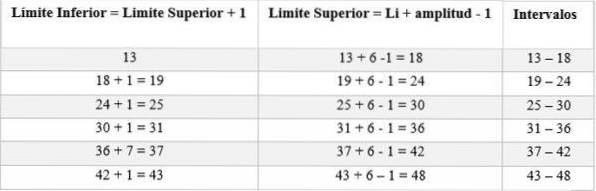
Vervolgens wordt de absolute frequentie berekend om het aantal mannen te bepalen dat overeenkomt met elk interval; in dit geval is het:
- Interval 1:13 - 18 = 9
- Interval 2:19 - 24 = 9
- Interval 3:25 - 30 = 5
- Interval 4:31 - 36 = 2
- Interval 5:37 - 42 = 2
- Bereik 6: 43 - 48 = 3
Bij het optellen van de absolute frequentie van elke klasse, moet deze gelijk zijn aan het totale aantal monsters; in dit geval 30.
Vervolgens wordt de relatieve frequentie van elk interval berekend, waarbij de absolute frequentie wordt gedeeld door het totale aantal waarnemingen:
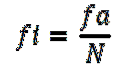
- Interval 1: fi = 9 ÷ 30 = 0,30
- Interval 2: fi = 9 ÷ 30 = 0,30
- Interval 3: fi = 5 ÷ 30 = 0,1666
- Interval 4: fi = 2 ÷ 30 = 0,0666
- Interval 5: fi = 2 ÷ 30 = 0,0666
- Interval 4: fi = 3 ÷ 30 = 0,10
Vervolgens kun je een tabel maken die de gegevens weergeeft, en ook het diagram van de relatieve frequentie in relatie tot de verkregen intervallen, zoals te zien is in de volgende afbeeldingen:
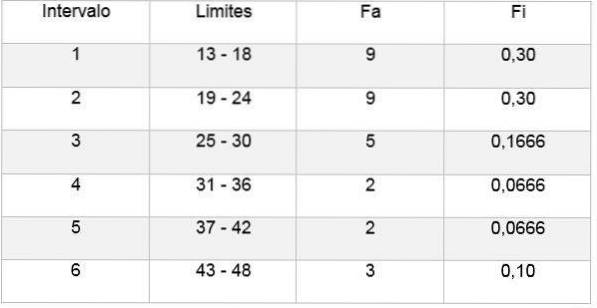
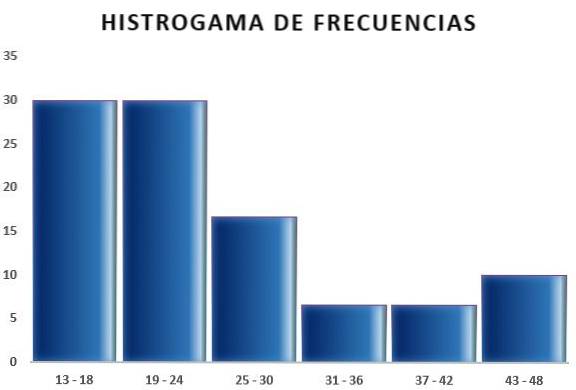
Op deze manier maakt de Sturges-regel het mogelijk het aantal klassen of intervallen te bepalen waarin een steekproef kan worden verdeeld, om een gegevenssteekproef samen te vatten door tabellen en grafieken uit te werken..
Referenties
- Alfonso Urquía, M. V. (2013). Modellering en simulatie van discrete gebeurtenissen. UNED,.
- Altman Naomi, M. K. (2015). "Eenvoudige lineaire regressie." Nature Methods .
- Antúnez, R. J. (2014). Statistieken in het onderwijs. Digitale EENHEID.
- Fox, J. (1997.). Toegepaste regressieanalyse, lineaire modellen en gerelateerde methoden. SAGE-publicaties.
- Humberto Llinás Solano, C. R. (2005). Beschrijvende statistieken en kansverdelingen. noordelijke universiteit.
- Panteleeva, O. V. (2005). Grondbeginselen van waarschijnlijkheid en statistiek.
- O. Kuehl, M. O. (2001). Ontwerp van experimenten: statistische principes van onderzoeksontwerp en analyse. Thomson Editors.



Niemand heeft nog op dit artikel gereageerd.