EEN empirische regel Het is het resultaat van praktische ervaring en observatie in het echte leven. Het is bijvoorbeeld mogelijk om te weten welke vogelsoorten op bepaalde plaatsen op elk moment van het jaar kunnen worden waargenomen en op basis van die waarneming kan een 'regel' worden opgesteld die de levenscycli van deze vogels beschrijft..
In statistieken verwijst de empirische regel naar de manier waarop waarnemingen zijn gegroepeerd rond een centrale waarde, het gemiddelde of gemiddelde, in eenheden van standaarddeviatie..
Stel dat je een groep mensen hebt met een gemiddelde lengte van 1,62 meter en een standaarddeviatie van 0,25 meter, dan zou je met de empirische regel bijvoorbeeld kunnen bepalen hoeveel mensen er in een interval van de gemiddelde plus of min één zouden zitten standaardafwijking?
Volgens de regel is 68% van de gegevens min of meer één standaarddeviatie van het gemiddelde, dat wil zeggen dat 68% van de mensen in de groep een lengte heeft tussen 1,37 (1,62-0,25) en 1,87 (1,62 + 0,25). meter.
Artikel index
De empirische regel is een generalisatie van de Tchebyshev-stelling en de normale verdeling.
De stelling van Tchebyshev zegt dat: voor een waarde van k> 1, de kans dat een willekeurige variabele valt tussen het gemiddelde minus k keer de standaarddeviatie en het gemiddelde plus k keer, de standaarddeviatie groter is dan of gelijk is aan (1 - 1 / ktwee.
Het voordeel van deze stelling is dat deze van toepassing is op discrete of continue willekeurige variabelen met elke kansverdeling, maar de regel die eruit wordt gedefinieerd is niet altijd erg nauwkeurig, omdat deze afhangt van de symmetrie van de verdeling. Hoe scheefder de verdeling van de willekeurige variabele, des te minder aangepast aan de regel zal zijn gedrag zijn.
De empirische regel die op basis van deze stelling is gedefinieerd, is:
Als k = √2, wordt er gezegd dat 50% van de gegevens zich in het interval bevinden: [µ - √2 s, µ + √2 s]
Als k = 2, wordt er gezegd dat 75% van de gegevens zich in het interval bevindt: [µ - 2 s, µ + 2 s]
Als k = 3, wordt er gezegd dat 89% van de gegevens zich in het interval bevindt: [µ - 3 s, µ + 3 s]
De normale verdeling, of Gaussiaanse bel, maakt het mogelijk om de empirische regel of regel 68-95-99,7 vast te stellen..
De regel is gebaseerd op de kans dat een willekeurige variabele voorkomt in intervallen tussen het gemiddelde minus één, twee of drie standaarddeviaties en het gemiddelde plus één, twee of drie standaarddeviaties..
De empirische regel definieert de volgende intervallen:
68,27% van de gegevens bevindt zich in het interval: [µ - s, µ + s]
95,45% van de gegevens bevindt zich in het interval: [µ - 2s, µ + 2s]
99,73% van de gegevens bevindt zich in het interval: [µ - 3s, µ + 3s]
In de figuur kun je zien hoe deze intervallen worden gepresenteerd en de relatie daartussen bij het vergroten van de breedte van de basis van de grafiek.
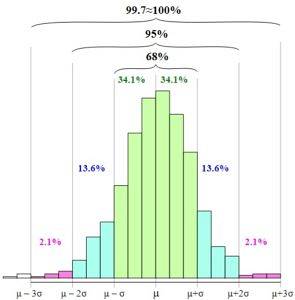
Daarom definieert de toepassing van de empirische regel op schaal van een standaard normaalvariabele, z, de volgende intervallen:
68,27% van de gegevens bevindt zich in het interval: [-1, 1]
95,45% van de gegevens bevindt zich in het interval: [-2, 2]
99,73% van de gegevens bevindt zich in het interval: [-3, 3]
De empirische regel maakt verkorte berekeningen mogelijk bij het werken met een normale verdeling.
Stel dat een groep van 100 studenten een gemiddelde leeftijd heeft van 23 jaar, met een standaarddeviatie van 2 jaar. Welke informatie staat de empirische regel toe?
Het toepassen van de empirische regel omvat de volgende stappen:
Omdat het gemiddelde 23 is en de standaarddeviatie 2, zijn de intervallen:
[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]
[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]
[µ - 3s, µ + 3s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]
(100) * 68,27% = 68 studenten ongeveer
(100) * 95,45% = 95 studenten ongeveer
(100) * 99,73% = ongeveer 100 studenten
Minstens 68 studenten zijn tussen de 21 en 25 jaar.
Minstens 95 studenten zijn tussen de 19 en 27 jaar oud.
Bijna 100 studenten zijn tussen de 17 en 29 jaar oud.
De empirische regel is een snelle en praktische manier om statistische gegevens te analyseren en wordt steeds betrouwbaarder naarmate de verdeling symmetrie nadert.
Het nut ervan hangt af van het vakgebied waarin het wordt gebruikt en de vragen die worden gesteld. Het is erg handig om te weten dat het voorkomen van waarden van drie standaarddeviaties onder of boven het gemiddelde bijna onwaarschijnlijk is, zelfs voor niet-normale verdelingsvariabelen, ligt ten minste 88,8% van de gevallen in het interval van drie sigma..
In de sociale wetenschappen is een algemeen sluitend resultaat het interval van het gemiddelde plus of min twee sigma (95%), terwijl in de deeltjesfysica een nieuw effect een interval van vijf sigma (99,99994%) vereist om als een ontdekking te worden beschouwd..
In een natuurreservaat leven naar schatting gemiddeld 16.000 konijnen met een standaarddeviatie van 500 konijnen. Als de verdeling van de variabele 'aantal konijnen in de reserve' onbekend is, is het mogelijk om de kans te schatten dat de konijnenpopulatie tussen de 15.000 en 17.000 konijnen ligt?
Het interval kan in deze termen worden weergegeven:
15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s
17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s
Daarom: [15000, 17000] = [µ - 2 s, µ + 2 s]
Als we de stelling van Tchebyshev toepassen, is de kans op zijn minst 0,75 dat de konijnenpopulatie in het natuurreservaat tussen de 15.000 en 17.000 konijnen ligt..
Het gemiddelde gewicht van eenjarige kinderen in een land wordt normaal verdeeld met een gemiddelde van 10 kilogram en een standaarddeviatie van ongeveer 1 kilogram.
a) Schat het percentage eenjarige kinderen in het land met een gemiddeld gewicht tussen 8 en 12 kilogram.
8 = 10 - 2 = 10 - 2 (1) = µ - 2 s
12 = 10 + 2 = 10 + 2 (1) = µ + 2 s
Daarom: [8, 12] = [µ - 2s, µ + 2s]
Volgens de empirische regel kan worden gesteld dat 68,27% van de eenjarige kinderen in het land tussen de 8 en 12 kilogram wegen.
b) Wat is de kans om een eenjarig kind te vinden dat 7 kilogram of minder weegt?
7 = 10 - 3 = 10 - 3 (1) = µ - 3 s
Het is bekend dat 7 kilogram gewicht de waarde µ - 3s vertegenwoordigt, en het is ook bekend dat 99,73% van de kinderen tussen de 7 en 13 kilogram weegt. Dat laat slechts 0,27% van het totale aantal kinderen over voor de extremen. De helft daarvan, 0,135%, is 7 kilogram of minder en de andere helft, 0,135%, is 11 kilogram of meer.
Er kan dus worden geconcludeerd dat er een kans van 0,00135 is dat een kind 7 kilogram of minder weegt.
c) Als de bevolking van het land 50 miljoen inwoners bereikt en 1-jarige kinderen 1% van de bevolking van het land vertegenwoordigen, hoeveel eenjarige kinderen wegen dan tussen de 9 en 11 kilogram?
9 = 10 - 1 = µ - s
11 = 10 + 1 = µ + s
Daarom: [9, 11] = [µ - s, µ + s]
Volgens de empirische regel bevindt 68,27% van de eenjarigen in het land zich in het interval [µ - s, µ + s]
Er zijn 500.000 eenjarigen in het land (1% van 50 miljoen), dus 341.350 kinderen (68,27% van 500.000) wegen tussen de 9 en 11 kilogram.
Niemand heeft nog op dit artikel gereageerd.