De wiskundige relatie is de link die bestaat tussen de elementen van een subset met betrekking tot het product van twee sets. EEN functie omvat de wiskundige bewerking om de waarde van een afhankelijke variabele te bepalen op basis van de waarde van een onafhankelijke variabele. Elke functie is een relatie, maar niet elke relatie is een functie.
| Relatie | Functie | |
|---|---|---|
| Definitie | Subset van bestelde paren die overeenkomen met het Cartesiaanse product van twee sets. | Wiskundige bewerking die moet worden uitgevoerd met de variabele X om de variabele te krijgen Y. |
| Notatie | X R Y X het is gerelateerd aan Y. | Y= ƒ (X Y is een functie van X. |
| Kenmerken |
|
|
| Voorbeelden |
|
|
Het heet de binaire relatie van een set A in een set B of de relatie tussen elementen van A en B tot elke subset C van het Cartesiaans product A x B.
Dat wil zeggen, als set A bestaat uit elementen 1, 2 en 3, en set B bestaat uit elementen 4 en 5, zal het Cartesiaanse product van A x B de geordende paren zijn:
EEN x B = (1,4), (2,4), (3, 4), (1,5), (2,5), (3,5).
De deelverzameling C = (2,4), (3,5) zal een relatie zijn van A en B aangezien deze is samengesteld uit de geordende paren (2,4) en (3, 5), het resultaat van de Cartesiaanse product van A x B.
"Laat A en B twee willekeurige niet-lege sets zijn, laat A x B de productset van beide zijn, dat wil zeggen: A x B wordt gevormd door de geordende paren (x, y) zodat X is het element van A en Y het is voor B. Als een deelverzameling C is gedefinieerd in A x B, wordt een binaire relatie in A en B automatisch als volgt bepaald:
X R Y als en slechts als (x, y) ∈ C
(de notatie X R Y Middelen "X het is gerelateerd aan Y.
We noemen set A startset en we noemen set B aankomst set.
De relatie domein zijn de elementen waaruit de startset bestaat, terwijl de verhouding bereik zijn de elementen van de aankomstset.
Set NAAR van X elementen van mannen in een populatie en B is de set van Y elementen van vrouwen uit dezelfde populatie. Een relatie komt tot stand wanneer "X is getrouwd met Y.
Als we het hebben over een wiskundige functie van een set A in een set B, verwijzen we naar een regel of mechanisme dat de elementen van set A relateert aan een element van set B.
'Sean X Y Y twee echte variabelen, wordt dat dan gezegd y is een functie van x ja tegen elke waarde die ik neem X komt overeen met een waarde van Y.
De onafhankelijke variabele is X terwijl Y is de afhankelijke variabele of functie:
y = ƒ (x)
De set waarin de X het heet domein van de functie (origineel) en de variatie van Y functiebereik (foto).
De set van paren (X, Y) zoals dat Y= ƒ (X) wordt genoemd functie grafiekals ze worden weergegeven in cartesiaanse assen, wordt een puntenfamilie geroepen functie grafiek.
In de wiskunde krijgen we veel voorbeelden van functies. Hier zijn voorbeelden van vlaggenschipfuncties.
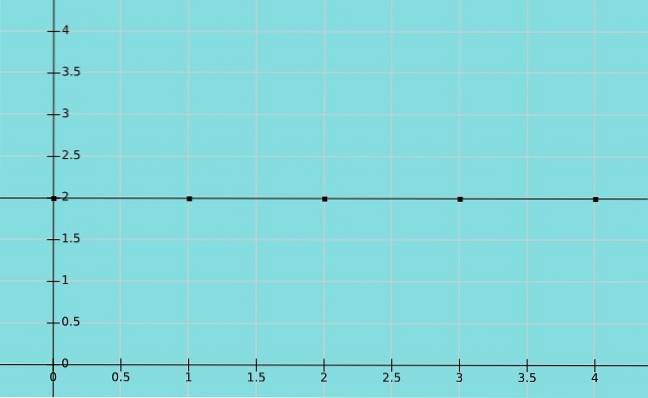
Een functie wordt constant genoemd als het element van set B dat overeenkomt met set A hetzelfde is. In dit geval komen alle waarden van x overeen met dezelfde waarde van y. Het domein is dus de reële getallen terwijl het bereik een constante waarde is.
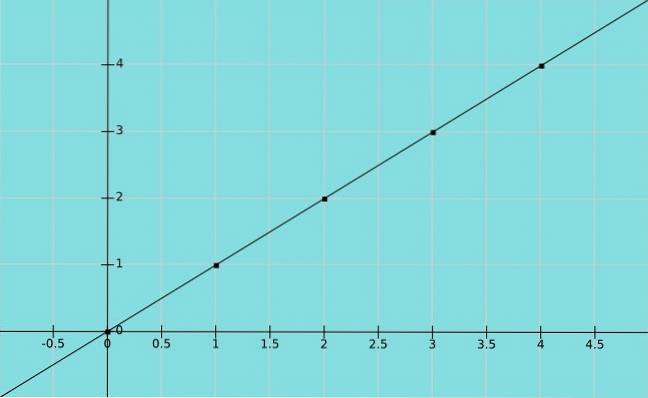
Laten we veronderstellen X is een variabele en dat Y heeft dezelfde waarde als X. We hebben dan een identiteitsfunctie y = x, waar de parenx, y) in de grafiek zijn (1,1), (2,2), (3,3) enzovoort.
Een polynoomfunctie vervult de vorm y = anXn+naarn-1+Xn-1+… + AtweeXtwee+naar1x + een0. De bovenstaande grafiek toont de functie ƒ (x) = xtwee+x-2.
Stel nu dat de afhankelijke variabele Y is gelijk aan de onafhankelijke variabele X verheven tot de kubus. We hebben de functie y = x3, waarvan de grafiek hieronder wordt weergegeven:
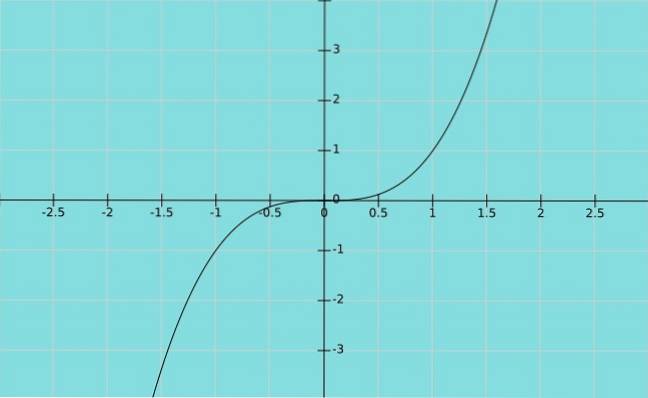
Niemand heeft nog op dit artikel gereageerd.