De halve cirkel is een vlakke figuur begrensd door een diameter van de omtrek en een van de twee platte cirkelbogen bepaald door die diameter.
Op deze manier wordt een halve cirkel begrensd door een halve omtrek, die bestaat uit een platte cirkelvormige boog en een recht segment dat de uiteinden van de platte cirkelvormige boog verbindt. De halve cirkel omvat de halve cirkel en alle punten erin..
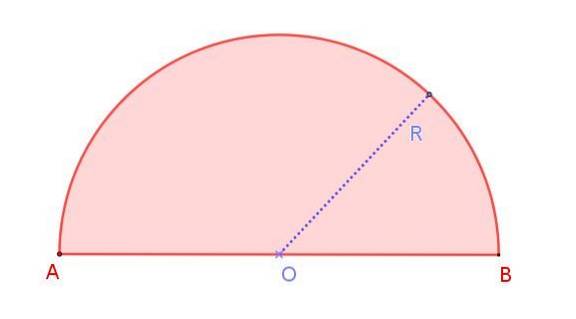
We kunnen dit zien in figuur 1, die een halve cirkel toont met straal R, waarvan de maat de helft is van die van diameter AB. Merk op dat in tegenstelling tot een cirkel, waarin er oneindige diameters zijn, er in de halve omtrek slechts één diameter is.
De halve cirkel is een geometrische figuur met veel toepassingen in architectuur en design, zoals we zien in de volgende afbeelding:
Artikel index
De elementen van een halve cirkel zijn:
1.- De vlakke cirkelboog A⌒B
2.- Het segment [AB]
3.- De punten binnen de halve cirkel die zijn samengesteld uit de boog A⌒B en het segment [AB].
De omtrek is de som van de contour van de boog plus die van het rechte segment, daarom:
Omtrek = booglengte A⌒B + segmentlengte [AB]
In het geval van een halve cirkel met straal R, wordt de omtrek P gegeven door de formule:
P = π⋅R + 2⋅R = (π + 2) ⋅R
De eerste term is de halve omtrek van een cirkel met straal R, terwijl de tweede de lengte van de diameter is, die tweemaal de straal is..
Aangezien een halve cirkel een van de vlakke hoeksectoren is die overblijven wanneer een diameter door de omtrek wordt getrokken, is het gebied A de helft van het gebied van de cirkel dat de halve cirkel met straal R bevat:
A = (π⋅Rtwee) / 2 = ½ π⋅Rtwee
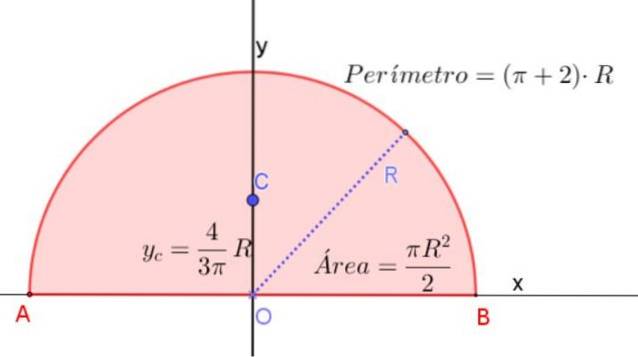
Het zwaartepunt van een halve cirkel is op zijn symmetrie-as op een hoogte gemeten vanaf de diameter van 4 / (3π) maal de straal R.
Dit komt overeen met ongeveer 0,424 ⋅R, gemeten vanaf het midden van de halve cirkel en op zijn symmetrieas, zoals weergegeven in figuur 3.
Het traagheidsmoment van een vlakke figuur ten opzichte van een as, bijvoorbeeld x-as, wordt gedefinieerd als:
De integraal van het kwadraat van de afstand van de punten die bij de figuur horen tot de as, waarbij het integratiedifferentiaal een oneindig klein gebiedselement is, genomen op de positie van elk punt.
Figuur 4 toont de definitie van het traagheidsmoment IX van de halve cirkel met straal R, ten opzichte van de X-as die door zijn diagonaal gaat:
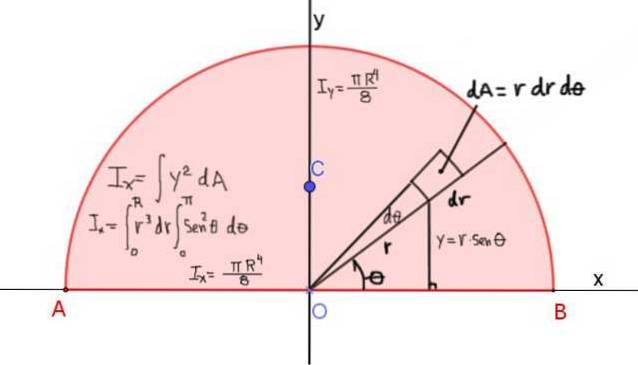
Het traagheidsmoment om de x-as wordt gegeven door:
ikX = (π⋅R4) / 8
En het traagheidsmoment ten opzichte van de symmetrieas y is:
Iy = (π⋅R4) / 8
Opgemerkt wordt dat beide traagheidsmomenten samenvallen in hun formule, maar het is belangrijk op te merken dat ze verwijzen naar verschillende assen.
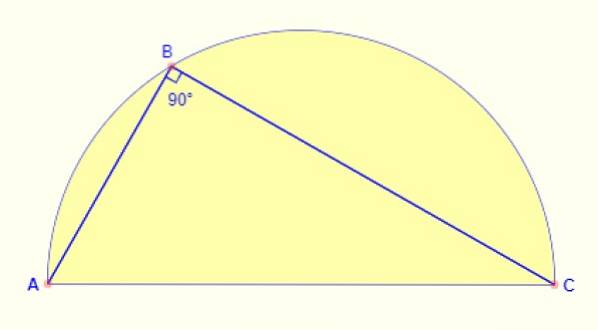
De hoek ingeschreven in de halve cirkel is altijd 90º. Ongeacht waar het punt op de boog wordt genomen, de hoek tussen de zijden AB en BC van de figuur is altijd goed..
Bepaal de omtrek van een halve cirkel met een straal van 10 cm.
Onthoud dat de omtrek als functie van de straal wordt gegeven door de formule die we eerder zagen:
P = (2 + π) ⋅R
P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.
Zoek de oppervlakte van een halve cirkel met een straal van 10 cm.
De formule voor de oppervlakte van een halve cirkel is:
A = ½ π⋅Rtwee = ½ π⋅ (10 cm)twee = 50π cmtwee = 50 x 3,14 cmtwee = 157 cmtwee.
Bepaal de hoogte h van het zwaartepunt van een halve cirkel met straal R = 10 cm gemeten vanaf de basis, waarbij de diameter van de halve cirkel hetzelfde is.
Het zwaartepunt is het evenwichtspunt van de halve cirkel en zijn positie is op de symmetrieas op een hoogte h vanaf de basis (diameter van de halve cirkel):
h = (4⋅R) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4,246 cm
Zoek het traagheidsmoment van een halve cirkel ten opzichte van de as die samenvalt met zijn diameter, wetende dat de halve cirkel is gemaakt van een dunne plaat. De straal is 10 cm en de massa is 100 gram.
De formule die het traagheidsmoment van de halve cirkel geeft, is:
ikX = (π⋅R4) / 8
Maar aangezien het probleem ons vertelt dat het een materiële halve cirkel is, moet de vorige relatie worden vermenigvuldigd met de oppervlaktedichtheid van de massa van de halve cirkel, die wordt aangeduid met σ.
ikX = σ (π⋅R4) / 8
We gaan dan verder met het bepalen van σ, wat niets anders is dan de massa van de halve cirkel gedeeld door zijn oppervlakte.
De oppervlakte werd bepaald in oefening 2 en het resultaat was 157 cmtwee. Dan is de oppervlaktedichtheid van deze halve cirkel:
σ = 100 gram / 157 cmtwee = 0,637 g / cmtwee
Dan wordt het traagheidsmoment ten opzichte van de diameter als volgt berekend:
ikX = (0,637 g / cmtwee) [3.1416 ⋅ (10 cm)4] / 8
Resulterend:
ikX = 2502 g⋅cmtwee
Bepaal het traagheidsmoment van een halve cirkel met een straal van 10 cm gemaakt van een materiaalplaat met een oppervlaktedichtheid van 0,637 g / cmtwee langs een as die door zijn zwaartepunt loopt en evenwijdig is aan zijn diameter.
Om deze oefening op te lossen, is het noodzakelijk om de stelling van Steiner over traagheidsmomenten van parallelle assen te onthouden, die zegt:
Het traagheidsmoment I ten opzichte van een as die zich op afstand h van het zwaartepunt bevindt is gelijk aan de som van het traagheidsmoment Ic met betrekking tot een as die door het zwaartepunt loopt en evenwijdig is aan de eerste plus het product van de massa maal het kwadraat van de scheiding van de twee assen.
Ik = ikc + M htwee
In ons geval is I bekend wat het traagheidsmoment is ten opzichte van de diameter, dat al berekend was in opgave 4. Ook is de scheiding h tussen de diameter en het zwaartepunt bekend, die berekend is in opgave 3.
We hoeven alleen Ic te wissen:
ikc = I - M utwee
ikc = 2502 g⋅cmtwee - 100g ⋅ (4,246 cm)twee waardoor het traagheidsmoment door een as evenwijdig aan de diameter en door het zwaartepunt loopt:
ikc = 699,15 g⋅cmtwee
Niemand heeft nog op dit artikel gereageerd.