Twee punten A en A 'hebben centrale symmetrie met betrekking tot een punt O wanneer het segment AA 'erdoorheen gaat en tevens het middelpunt van AA' is. Punt O wordt genoemd centrum van symmetrie.
De centrale symmetrie van een driehoek ABC ten opzichte van een punt O, is een andere driehoek A'B'C 'die de volgende kenmerken heeft:
-Homologe segmenten hebben dezelfde lengte
-Hun overeenkomstige hoeken hebben dezelfde maat.
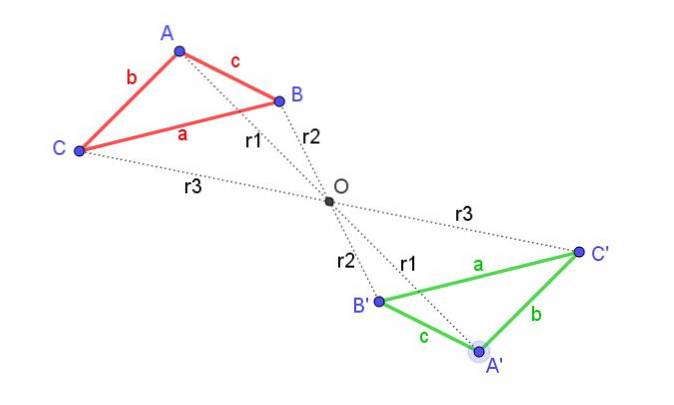
In figuur 1 zie je een driehoek ABC (rood) en zijn centrale symmetrie A'B'C '(groen), ten opzichte van het symmetriecentrum O.
In dezelfde figuur zou een oplettende waarnemer zich realiseren dat hetzelfde resultaat wordt verkregen door een rotatie van de oorspronkelijke driehoek toe te passen, zolang deze maar 180 ° is en gecentreerd in O.
Daarom is een centrale symmetrie gelijk aan een draai van 180º ten opzichte van het symmetriecentrum.
Artikel index
Een centrale symmetrie heeft de volgende eigenschappen:
-Het symmetriecentrum is het middelpunt van het segment dat een punt met zijn symmetrie verbindt.
-Een symmetrisch punt van een ander dat in het midden van symmetrie ligt, valt samen met het midden van symmetrie.
-De centrale symmetrie van een driehoek is een driehoek die congruent (gelijk) is aan het origineel.
-Het beeld door centrale symmetrie van een cirkel is een andere cirkel met gelijke straal.
-Een cirkel heeft centrale symmetrie rond zijn eigen middelpunt.
-De ellips heeft centrale symmetrie rond het midden.
-Een segment heeft centrale symmetrie rond het middelpunt.
-De gelijkzijdige driehoek heeft geen centrale symmetrie ten opzichte van het midden, omdat de symmetrie, hoewel congruent met de eerste, een geroteerde gelijkzijdige driehoek geeft.
-Vierkanten hebben centrale symmetrie rond hun middelpunt.
-Een vijfhoek mist centrale symmetrie rond zijn middelpunt.
-Regelmatige veelhoeken hebben centrale symmetrie als ze een even aantal zijden hebben.
Symmetriecriteria hebben veel toepassingen in wetenschap en techniek. Centrale symmetrie is aanwezig in de natuur, bijvoorbeeld ijskristallen en spinnenwebben hebben dit soort symmetrie.
Bovendien zijn veel problemen gemakkelijk op te lossen als er gebruik wordt gemaakt van de aanwezigheid van centrale symmetrie en andere soorten symmetrie. Daarom is het handig om snel te identificeren wanneer het zich voordoet.
Gegeven een punt P van coördinaten (a, b), moeten we de coördinaten vinden van zijn symmetrische P 'ten opzichte van de oorsprong O van coördinaten (0, 0).
Het eerste is om het punt P 'te construeren, waarvoor een lijn wordt getrokken die door de oorsprong O en door het punt P loopt. De vergelijking van die lijn is y = (b / a) x.
Laten we nu (a ', b') de coördinaten van het symmetrische punt P 'noemen. Het punt P 'moet op de lijn liggen die door O loopt en daarom is het waar: b' = (b / a) a '. Verder moet de afstand OP gelijk zijn aan OP ', wat in analytische vorm als volgt is geschreven:
√ (tottwee + btwee) = √ (een 'twee + b 'twee
Het volgende is om b '= [(b / a) .a'] in de bovenstaande uitdrukking te vervangen en beide zijden van de gelijkheid te kwadrateren om de vierkantswortel te elimineren: (atwee + btwee) = [een 'twee + (btwee/naartwee).naar'twee
Door een gemeenschappelijke factor te extraheren en te vereenvoudigen, krijgen we dat een 'twee = eentwee. Deze vergelijking heeft twee echte oplossingen: a '= + a of a' = -a.
Om b 'te krijgen, gebruiken we opnieuw b' = (b / a) a '. Als de positieve oplossing van a 'wordt vervangen, komen we uit op dat b' = b. En als de negatieve oplossing wordt vervangen, dan is b '= -b.
De positieve oplossing geeft voor P 'hetzelfde punt P, dus het wordt weggegooid. De negatieve oplossing geeft zeker de coördinaten van het symmetrische punt:
P ': (-a, -b)
Het is vereist om aan te tonen dat een segment AB en zijn centrale symmetrische A'B 'dezelfde lengte hebben.
Beginnend met de coördinaten van punt A, die (Ax, Ay) zijn en die van punt B: (Bx, By), wordt de lengte van segment AB gegeven door:
d (AB) = √ ((Bx - Ax)twee + (Door - Ay)twee
Naar analogie zal het symmetrische segment A'B 'de lengte hebben die wordt gegeven door:
d (A'B ') = √ ((Bx' - Ax ')twee + (Door '- Ay')twee
De coördinaten van het symmetrische punt A 'zijn Ax' = -Ax en Ay '= -Ay. Evenzo zijn die van B 'Bx' = -Bx en By '= -By. Als deze coördinaten worden vervangen in de vergelijking van de afstand d (A'B '), hebben we:
d (A'B ') = √ ((-Bx + Ax)twee + (-Door + Ay)twee) wat gelijk staat aan:
√ ((Bx - Bijl)twee + (Door - Ay)twee) = d (AB)
Zo wordt aangetoond dat beide segmenten dezelfde lengte hebben.
Laat analytisch zien dat de centrale symmetrische O van een cirkel met straal R en middelpunt O dezelfde originele cirkel is.
De vergelijking van een cirkel met straal R en middelpunt O (0,0) is:
Xtwee + Ytwee = Rtwee (Vergelijking van de omtrek C)
Als op elk punt P van de omtrek y van coördinaten (x, y) de symmetrische P 'van coördinaten (x', y ') wordt gevonden, is de vergelijking van de symmetrische omtrek:
x 'twee + Y 'twee = Rtwee (Vergelijking van de symmetrische cirkel C ')
Nu verwijzen we naar het resultaat van voorbeeld 1, waarin geconcludeerd wordt dat de coördinaten van een punt P ', symmetrisch met P en met coördinaten (a, b), (-a, -b).
Maar in deze oefening heeft punt P coördinaten (x, y), dus de symmetrische P 'heeft coördinaten x' = -x en y '= -y. Als we dit in de vergelijking van de symmetrische cirkel vervangen, hebben we:
(-X)twee + (-J)twee = Rtwee
Wat gelijk is aan: xtwee+ Ytwee = Rtwee, concluderen dat de centrale symmetrie van een cirkel ten opzichte van het middelpunt de omtrek zelf is.
Laat geometrisch zien dat centrale symmetrie hoeken behoudt.
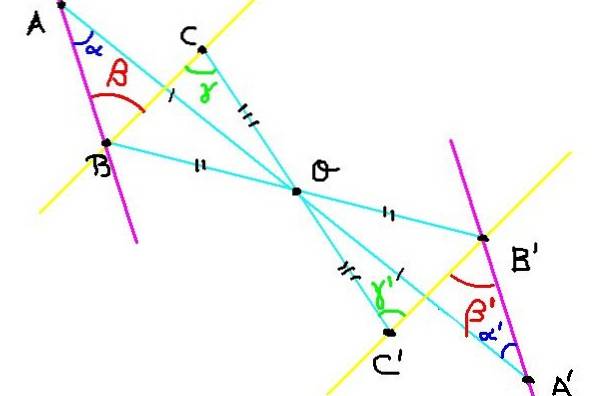
Er zijn drie punten A, B en C in het vliegtuig. De symmetrieën A ', B' en C 'zijn geconstrueerd ten opzichte van het symmetriecentrum O, zoals weergegeven in figuur 4.
Nu moeten we aantonen dat de hoek ∡ABC = β dezelfde maat heeft als de hoek ∡A'B'C '= β'.
Omdat C en C 'symmetrisch zijn, is OC = OC'. Evenzo OB = OB 'en OA = OA'. Aan de andere kant is de hoek ∡BOC = ∡B'OC 'omdat ze tegengesteld zijn aan het hoekpunt.
Dan zijn de driehoeken BOC en B'OC 'congruent omdat ze een gelijke hoek hebben tussen twee gelijke zijden.
Omdat BOC congruent is met B'OC ', zijn de hoeken γ Y γ ' Ze zijn gelijk. Maar deze invalshoeken vervullen niet alleen γ = γ ' zijn interne afwisselend lijnen BC en B'C 'wat impliceert dat lijn BC evenwijdig is aan B'C'.
Evenzo is BOA congruent met B'OA ', waaruit het volgt α = α ' . Maar α Y α ' zijn afwisselende binnenhoeken tussen de lijnen BA en B'A ', waaruit wordt geconcludeerd dat lijn BA evenwijdig is aan B'A'.
Aangezien de hoek ∡ABC = β zijn zijden evenwijdig heeft met de hoek ∡A'B'C '= β' en ook beide scherp zijn, wordt geconcludeerd dat:
∡ABC = ∡A'B'C '= β = β'
Op deze manier bewijzen dat de centrale symmetrie de maat van de hoeken behoudt.
Niemand heeft nog op dit artikel gereageerd.