
Octale systeemgeschiedenis, nummeringssysteem, conversies
De octaal systeem een basis-acht (8) positioneel nummeringssysteem is; dat wil zeggen, het bestaat uit acht cijfers, namelijk: 0, 1, 2, 3, 4, 5, 6 en 7. Daarom kan elk cijfer van een octaal getal een waarde tussen 0 en 7 hebben. De octale getallen worden gevormd van binaire getallen.
Dit komt omdat de basis een exacte macht van twee (2) is. Dat wil zeggen, de nummers die tot het octale systeem behoren, worden gevormd wanneer ze worden gegroepeerd in drie opeenvolgende cijfers, gerangschikt van rechts naar links, waardoor hun decimale waarde wordt verkregen..

Artikel index
- 1 Geschiedenis
- 2 Octaal nummeringssysteem
- 3 Conversie van octaal naar decimaal systeem
- 3.1 Voorbeeld 1
- 3.2 Voorbeeld 2
- 4 Conversie van decimaal naar octaal systeem
- 4.1 Voorbeeld
- 5 Conversie van octaal naar binair systeem
- 6 Conversie van binair naar octaal systeem
- 7 Conversie van octaal naar hexadecimaal en vice versa
- 7.1 Voorbeeld
- 8 referenties
Verhaal
Het octale systeem vindt zijn oorsprong in de oudheid, toen mensen hun handen gebruikten om dieren van acht tot acht te tellen.
Om bijvoorbeeld het aantal koeien in een stal te tellen, begon men met de rechterhand te tellen, waarbij de duim met de pink werd samengevoegd; om het tweede dier te tellen werd de duim samengevoegd met de wijsvinger, en zo verder met de resterende vingers van elke hand, tot het voltooien van 8.
Er is de mogelijkheid dat in de oudheid het octale nummeringsysteem werd gebruikt vóór het decimaalteken om intercijferige spaties te kunnen tellen; d.w.z. tel alle vingers behalve duimen.
Later werd het octale nummeringsysteem opgericht, dat voortkwam uit het binaire systeem, omdat het veel cijfers nodig heeft om slechts één nummer weer te geven; vanaf dat moment werden de octale en hexagonale systemen gecreëerd, die niet zoveel cijfers nodig hebben en gemakkelijk kunnen worden geconverteerd naar het binaire systeem.
Octaal nummeringssysteem
Het octale systeem bestaat uit acht cijfers die lopen van 0 tot 7. Deze hebben dezelfde waarde als in het geval van het decimale systeem, maar hun relatieve waarde verandert afhankelijk van de positie die ze innemen. De waarde van elke positie wordt gegeven door de machten van basis 8.
De posities van de cijfers in een octaal getal hebben de volgende gewichten:
84, 83, 8twee, 81, 80, octaal punt, 8-1, 8-twee, 8-3, 8-4, 8-5.
Het grootste octale cijfer is 7; op deze manier wordt bij het tellen in dit systeem de positie van een cijfer verhoogd van 0 naar 7. Wanneer 7 is bereikt, wordt het teruggebracht naar 0 voor de volgende telling; op deze manier wordt de volgende cijferpositie opgehoogd. Om reeksen bijvoorbeeld te tellen, zal het in het octale systeem zijn:
- 0, 1, 2, 3, 4, 5, 6, 7, 10.
- 53, 54, 55, 56, 57, 60.
- 375, 376, 377, 400.
Er is een fundamentele stelling die wordt toegepast op het octale systeem en deze wordt als volgt uitgedrukt:
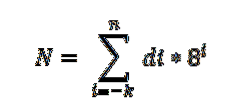
In deze uitdrukking staat di voor het cijfer vermenigvuldigd met de macht van grondtal 8, wat de plaatswaarde van elk cijfer aangeeft, op dezelfde manier als het is geordend in het decimale systeem.
U hebt bijvoorbeeld het nummer 543,2. Om het naar het octale systeem te brengen, wordt het als volgt onderverdeeld:
N = ∑ [(5 8twee) + (4 81) + (3 80) + (2 8-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0,125)
N = 320 +32 + 2 + 0,25 = 354 + 0,25d
Op die manier moet je 543,2wat = 354,25d. Het subscript q geeft aan dat het een octaal getal is dat ook kan worden weergegeven door het getal 8; en het subscript d verwijst naar het decimale getal, dat ook kan worden weergegeven door het getal 10.
Conversie van octaal naar decimaal systeem
Als u een getal van het octale systeem naar het equivalent in het decimale systeem wilt converteren, hoeft u alleen maar elk octaal cijfer te vermenigvuldigen met de plaatswaarde, beginnend vanaf de rechterkant.
voorbeeld 1
7328 = (7 8twee) + (3 81) + (2 80) = (7 64) + (3 8) + (2 1)
7328= 448 +24 +2
7328= 47410
Voorbeeld 2
26,98 = (2 81) + (6 80) + (9 8-1) = (2 8) + (6 1) + (9 0,125)
26,98 = 16 + 6 + 1,125
26,98= 23.12510
Conversie van decimaal naar octaal systeem
Een decimaal geheel getal kan worden geconverteerd naar een octaal getal met behulp van de herhaalde deelmethode, waarbij het decimale gehele getal wordt gedeeld door 8 totdat het quotiënt gelijk is aan 0, en de restanten van elke deling vertegenwoordigen het octale getal..
De residuen worden geordend van de laatste naar de eerste; dat wil zeggen, de eerste rest is het minst significante cijfer van het octale getal. Op die manier is het meest significante cijfer de laatste rest..
Voorbeeld
Octaal met decimaal getal 26610
- Deel het decimale getal 266 door 8 = 266/8 = 33 + rest van 2.
- Verdeel vervolgens de 33 door 8 = 33/8 = 4 + rest van 1.
- Verdeel 4 door 8 = 4/8 = 0 + rest van 4.
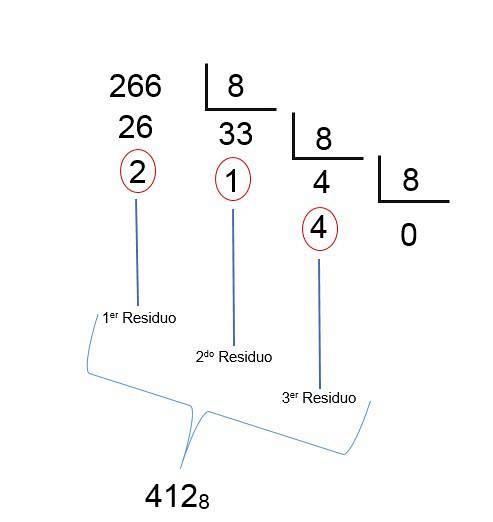
Omdat met de laatste deling een quotiënt kleiner dan 1 wordt verkregen, betekent dit dat het resultaat is gevonden; Je hoeft de restanten alleen omgekeerd te ordenen, zodanig dat het octale getal van 266 decimaal 412 is, zoals te zien is in de volgende afbeelding:
Conversie van octaal naar binair systeem
Conversie van octaal naar binair wordt gedaan door het octale cijfer om te zetten in het equivalente binaire cijfer, bestaande uit drie cijfers. Er is een tabel die laat zien hoe de acht mogelijke cijfers worden omgezet:
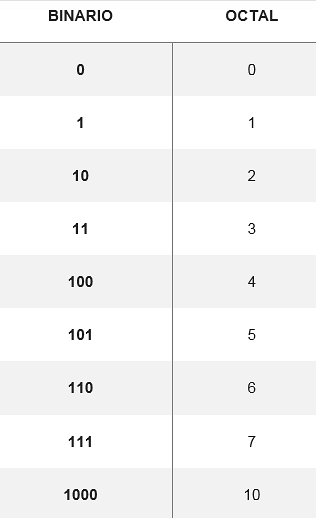
Van deze conversies kunt u elk getal van het octale systeem naar binair wijzigen, bijvoorbeeld om het getal 572 te converteren8 hun equivalenten worden in de tabel doorzocht. Het moet dus:
58 = 101
78= 111
twee8 = 10
Daarom 5728 is equivalent in het binaire systeem met 10111110.
Omzetten van binair naar octaal
Het proces van het omzetten van binaire gehele getallen naar octale gehele getallen is de omgekeerde bewerking van het vorige proces.
Dat wil zeggen, de bits van het binaire getal zijn gegroepeerd in twee groepen van drie bits, beginnend van rechts naar links. Vervolgens wordt de conversie van binair naar octaal gedaan met de vorige tabel.
In sommige gevallen heeft het binaire getal geen groepen van 3 bits; om het te voltooien, worden een of twee nullen links van de eerste groep toegevoegd.
Om bijvoorbeeld het binaire getal 11010110 in octaal te veranderen, doet u het volgende:
- Groepen van 3 bits worden gevormd beginnend van rechts (laatste bit):
11010110
- Omdat de eerste groep onvolledig is, wordt een voorloopnul toegevoegd:
011010110
- De conversie is gemaakt vanaf de tabel:
011 = 3
010 = 2
110 = 6
Het binaire getal 011010110 is dus gelijk aan 3268.
Omzetten van octaal naar hexadecimaal en vice versa
Om van een octaal getal naar het hexadecimaal systeem of van hexadecimaal naar octaal te wisselen, moet het getal eerst naar binair en vervolgens naar het gewenste systeem worden geconverteerd..
Hiervoor is er een tabel waarin elk hexadecimaal cijfer wordt weergegeven met zijn equivalent in het binaire systeem, bestaande uit vier cijfers.
In sommige gevallen heeft het binaire getal geen groepen van 4 bits; om het te voltooien, worden een of twee nullen links van de eerste groep toegevoegd
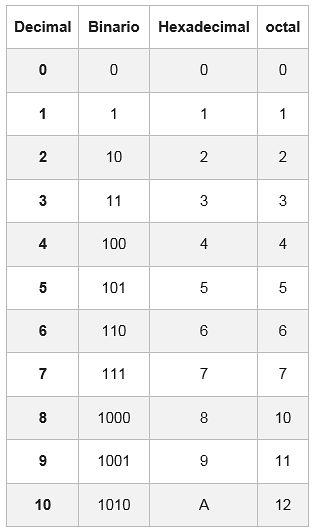
Voorbeeld
Converteer octaal getal 1646 naar hexadecimaal getal:
- Converteer het getal van octaal naar binair
18 = 1
68 = 110
48 = 100
68 = 110
- Dus 16468 = 1110100110.
- Om van binair naar hexadecimaal te converteren, worden ze eerst geordend in een groep van 4 bits, beginnend van rechts naar links:
11 1010 0110
- De eerste groep wordt aangevuld met nullen, zodat deze uit 4 bits kan bestaan:
0011 1010 0110
- De conversie vindt plaats van het binaire naar hexadecimale systeem. De equivalenties worden vervangen door middel van de tabel:
0011 = 3
1010 = A
0110 = 6
Het octale getal 1646 is dus gelijk aan 3A6 in het hexadecimale systeem..
Referenties
- Bressan, A. E. (1995). Inleiding tot nummeringsystemen. Argentijnse University of Business.
- Harris, J. N. (1957). Inleiding tot de binaire en octale nummeringsystemen: Lexington, Mass. Armed Services Technical Information Agency.
- Kumar, A. A. (2016). Grondbeginselen van digitale schakelingen. Leren Pvt.
- Peris, X. C. (2009). Single Operative Systemen.
- Ronald J. Tocci, N.S. (2003). Digitale systemen: principes en toepassingen. Pearson Education.



Niemand heeft nog op dit artikel gereageerd.