
Vaste deeltjes van omwentelingsvolume, typen, opgeloste oefeningen
De solide van revolutie Het is de driedimensionale figuur die wordt gegenereerd door een plat oppervlak rond de axiale as of omwentelingsas te roteren. Figuur 1 toont een animatie van een op deze manier gegenereerde revolutie.
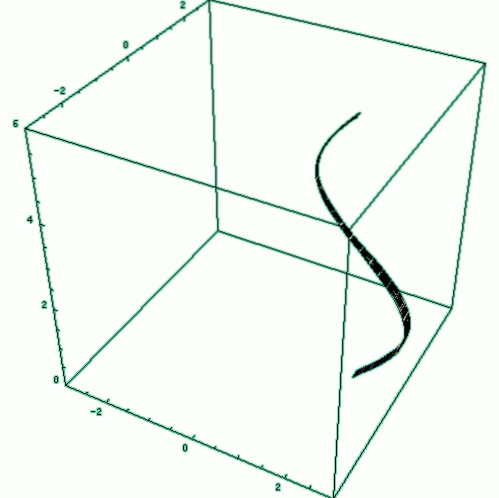
Een ander zeer gemakkelijk te visualiseren voorbeeld bestaat uit het genereren van een rechter cirkelvormige cilinder, waarbij een rechthoek van hoogte of lengte h en straal r rond de positieve x-as wordt gedraaid (figuur 2). Om het volume te vinden, is er een bekende formule:
V = oppervlakte van basis x hoogte
Andere omwentelingslichamen zijn de bol, de rechter cirkelvormige kegel en verschillende figuren, afhankelijk van het in rotatie gebrachte oppervlak en natuurlijk de geselecteerde as..
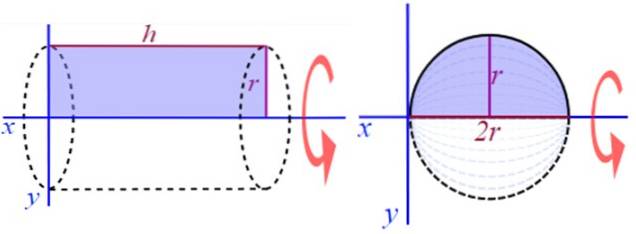
Het roteren van de halve cirkel rond een lijn evenwijdig aan de diameter geeft bijvoorbeeld een holle omwenteling.
Voor de cilinder, de kegel, de bol, zowel massief als hol, zijn er formules om het volume te vinden, afhankelijk van de straal en de hoogte. Maar wanneer ze worden gegenereerd door andere oppervlakken, wordt het volume berekend door welomlijnde integralen.
Artikel index
- 1 Soorten omwentelingslichamen
- 1.1 Bol
- 1.2 Kegel
- 1.3 cilinder
- 1.4 ringkern
- 2 Methoden voor het berekenen van het volume van een omwentelingslichaam
- 2.1 Schijf- of sluitringmethode
- 2.2 Laagmethode
- 3 Oefening opgelost
- 4 referenties
Soorten revolutie-lichamen
Revolutie-lichamen kunnen worden geclassificeerd volgens de curve die ze genereert:
Gebied
Het is voldoende om een halve cirkel rond een as te draaien die de diameter van de bol met straal R zal zijn.Het volume is:
V.gebied = (4/3) πR3
Ijshoorntje
Om een kegel met hoogte H en straal R te verkrijgen, is het te roteren oppervlak een rechthoekige driehoek rond de axiale as die door een van de benen loopt. Het volume is:
V.ijshoorntje = (1/3) πHRtwee
Cilinder
Door een rechthoek rond een axiale as te draaien die door een van de zijden gaat, wat de korte of de lange zijde kan zijn, krijgen we een rechter cirkelvormige cilinder met straal R en hoogte H, waarvan het volume is:
V.cilinder = πRtweeH.
Ringkern
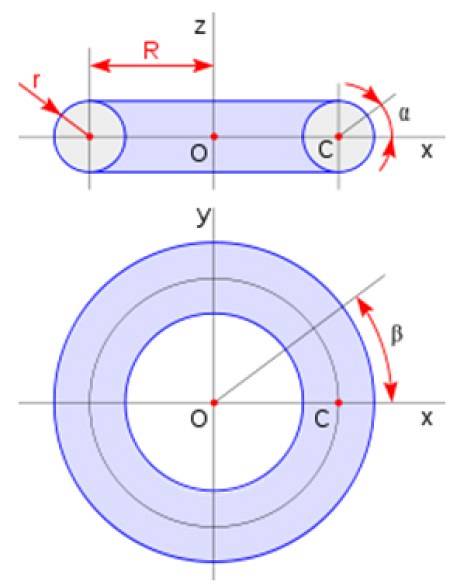
De torus heeft de vorm van een donut. Het wordt verkregen door een cirkelvormig gebied rond een lijn in het vlak te draaien die de cirkel niet snijdt. Het volume wordt gegeven door:
V.torus = 2πatweeR
Waar a is de straal van de doorsnede en R is de straal van de torus volgens het schema in de afbeelding:
Methoden voor het berekenen van het volume van een omwentelingslichaam
In integraalrekening komen deze twee methoden vaak voor:
-Schijven en ringen
-Schelpen
Schijf- of sluitringmethode
Bij het snijden van een omwentelingslichaam kan de doorsnede een schijf zijn, als de vaste stof massief is, of het kan een soort ring zijn (een schijf met een gat in het midden), als het een holle vaste stof is..
Stel dat een vlak gebied om de horizontale as wordt geroteerd. Uit dit vlakke gebied nemen we een kleine rechthoek met breedte Δx, die loodrecht rond de axiale as wordt geroteerd.
De hoogte van de rechthoek ligt tussen de buitenste kromme R (x) en de binnenste kromme r (x). Ze komen overeen met respectievelijk de buitenste straal en de binnenste straal..
Door deze rotatie te maken wordt een ring met volume ΔV gegenereerd, gegeven door:
ΔV = volledig volume - volume van het gat (indien aanwezig)
Onthoud dat het volume van een rechter cirkelvormige cilinder π is. radio-twee x hoogte hebben we:
ΔV = π [Rtwee(x) - rtwee(x)] Ax
De vaste stof kan worden verdeeld in een groot aantal kleine volumedeelten AV. Als we ze allemaal toevoegen, hebben we het volledige volume.
Om dit te doen, laten we het volume ΔV neigen naar 0, waarmee Δx ook heel klein wordt en een differentiële dx wordt.
Dus we hebben een integraal:
V = ∫naarb π [Rtwee(x) - rtwee(x)] dx
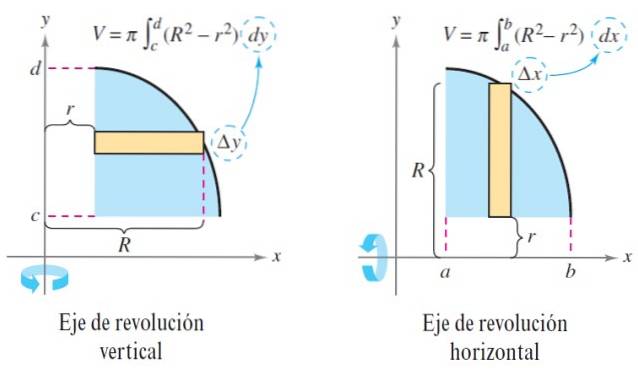
In het geval dat de vaste stof solide is, dan is de functie r (x) = 0, de plak van de vaste stof die wordt gegenereerd is een schijf en het volume blijft:
V = ∫naarb πRtwee(x) dx
Wanneer de omwentelingsas verticaal is, hebben de bovenstaande vergelijkingen de vorm:
V = ∫naarb π [Rtwee (y) - rtwee (y)] dy y V = ∫naarb πRtwee(y) dy
Laag methode
Zoals de naam al aangeeft, bestaat deze methode erin aan te nemen dat de vaste stof bestaat uit lagen met verschillende dikte. De laag is een dunne buis die ontstaat door de rotatie van een rechthoek evenwijdig aan de rotatieas.
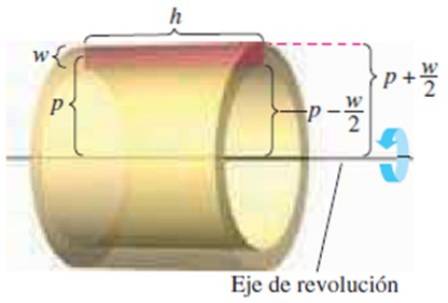
We hebben de volgende afmetingen:
-De hoogte van de rechthoek w
-Zijn lengtegraad h
-De afstand van het midden van de rechthoek tot de rotatieas p
Weten dat het volume van de laag is buitenvolume - binnenvolume
π (p + w / 2)tweeh - π (p - w / 2)tweeh
Door opmerkelijke producten te ontwikkelen en te vereenvoudigen, krijgt u:
Laagvolume = 2π⋅p⋅w⋅h
Laten we nu de hoogte w van de rechthoek Δy maken, zoals te zien is in de volgende afbeelding:
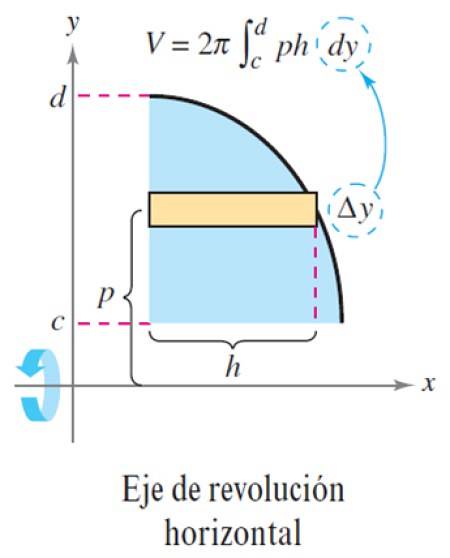
Hiermee is het volume ΔV:
ΔV = 2π p x h x Δy
En het aantal lagen maken n is erg groot, Δy wordt een differentiële dy, waarmee het totale volume de integraal is:
V = ∫cd 2π p (y) h (y) dy
De beschreven procedure is op soortgelijke wijze van toepassing wanneer de omwentelingsas verticaal is:
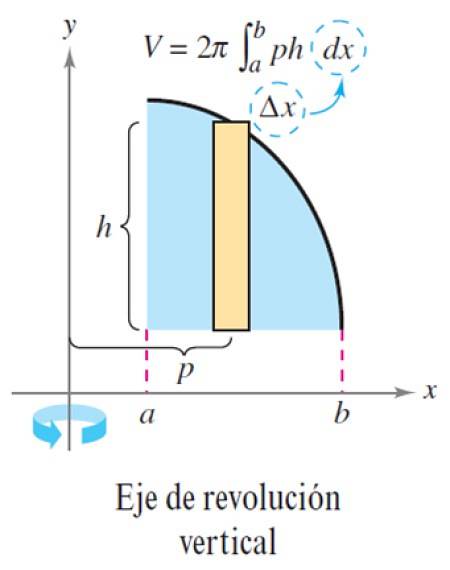
Oefening opgelost
Zoek het volume dat wordt gegenereerd door de rotatie van het vlakke gebied tussen de curven:
y = xtwee y = 0; x = 2
Rond de y-as.
Oplossing
-Het eerste dat we moeten doen, is het gebied dat het omwentelingslichaam zal genereren in een grafiek uitzetten en de rotatieas aangeven. We hebben het in de volgende grafiek:
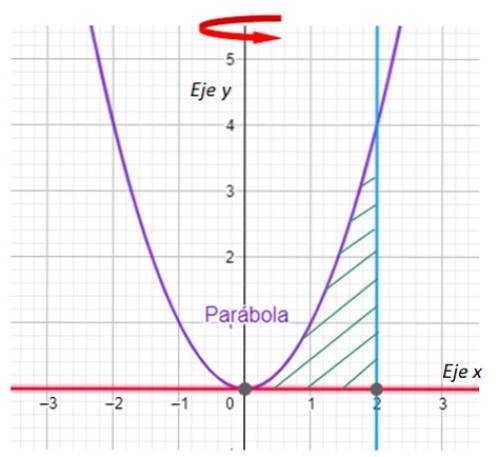
-Nu zoeken we de snijpunten tussen de kromme y = xtwee en de lijn x = 2. Van zijn kant is de lijn y = 0 niets anders dan de x-as.
Uit de grafiek is gemakkelijk te zien dat de parabool en de lijn elkaar snijden op het punt (2,4), wat wordt bevestigd door x = 2 te vervangen in y = xtwee.
-Vervolgens wordt gekozen voor een van de methodes om het volume te berekenen, bijvoorbeeld de lagenmethode met verticale omwentelingsas:
V = ∫naarb 2π p (x) h (x) dx
Stap 1: teken de rechthoek
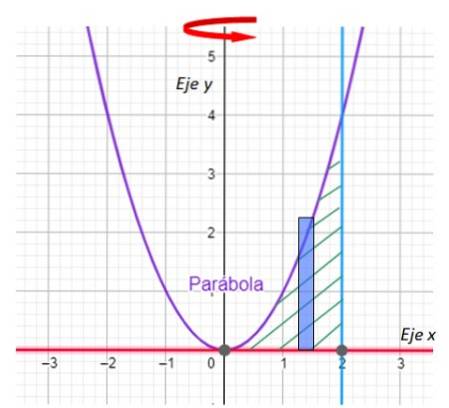
Belangrijk: Bij de laagjesmethode is de lange zijde van de rechthoek evenwijdig aan de rotatieas.
Stap 2: bepaal p (x)
De straal van de laag is X
Stap 3: bepaal h (x)
De hoogte van de rechthoek wordt bepaald door de parabool xtwee.
Stap 4: stel de volume-integraal vast en los deze op
De integratievariabele is x, die varieert tussen 0 en 2, hiermee hebben we de integratiegrenzen. Vervanging van de uitdrukkingen voor p (x) en h (x)

Referenties
- Larson, R. 2010. Berekening van een variabele. 9e. Editie. Mcgraw heuvel.
- Purcell, E. 2007. Calculus met analytische meetkunde. 9e. Editie. Pearson Education.
- Wikipedia. Solide van revolutie. Hersteld van: en.wikipedia.org.
- Wikipedia. Ringkern Hersteld van: es.wikipedia.org.
- Wolfram MathWorld. Solide van revolutie. Hersteld van: mathworld.wolfram.com.



Niemand heeft nog op dit artikel gereageerd.