
De theoremavergelijking, toepassingen en opgeloste oefening van Bernoulli
De De stelling van Bernoulli, die het gedrag van een vloeistof in beweging beschrijft, werd verkondigd door de wiskundige en natuurkundige Daniel Bernoulli in zijn werk Hydrodynamica. Volgens het principe zal een ideale vloeistof (zonder wrijving of viscositeit) die door een gesloten leiding circuleert, een constante energie op zijn pad hebben.
De stelling kan worden afgeleid uit het principe van behoud van energie en zelfs uit de tweede bewegingswet van Newton. Bovendien stelt het principe van Bernoulli ook vast dat een toename van de snelheid van een vloeistof een afname inhoudt van de druk waaraan het wordt blootgesteld, een afname van zijn potentiële energie, of beide tegelijkertijd..

De stelling heeft veel verschillende toepassingen, zowel in de wetenschappelijke wereld als in het dagelijks leven van mensen..
De gevolgen zijn onder meer aanwezig in de liftkracht van vliegtuigen, in de schoorstenen van huizen en industrieën, in waterleidingen..
Artikel index
- 1 Bernoulli's vergelijking
- 1.1 Vereenvoudigde vorm
- 2 Toepassingen
- 3 Oefening opgelost
- 4 referenties
Bernoulli's vergelijking
Hoewel Bernoulli degene was die afleidde dat de druk afneemt wanneer de stroomsnelheid toeneemt, is de waarheid dat het Leonhard Euler was die de Bernoulli-vergelijking daadwerkelijk heeft ontwikkeld in de vorm waarin deze tegenwoordig bekend is..
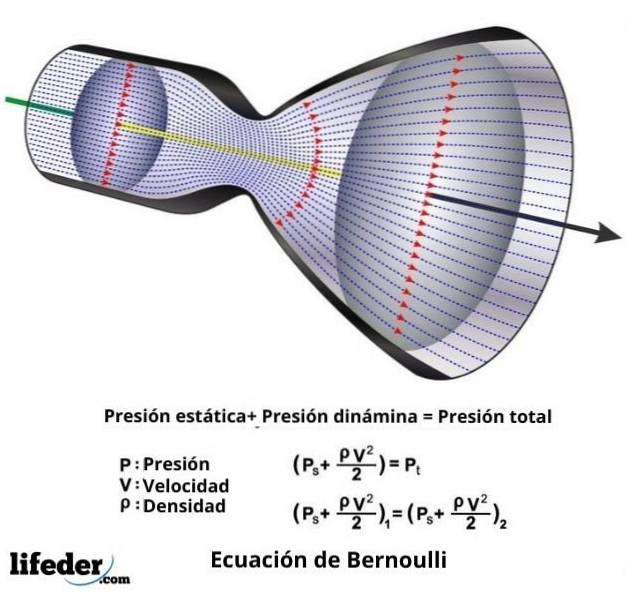
In ieder geval is de vergelijking van Bernoulli, die niets meer is dan de wiskundige uitdrukking van zijn stelling, de volgende:
vtwee ∙ ƿ / 2 + P + ƿ ∙ g ∙ z = constant
In deze uitdrukking is v de snelheid van de vloeistof door de beschouwde sectie, ƿ is de dichtheid van de vloeistof, P is de druk van de vloeistof, g is de waarde van de versnelling van de zwaartekracht, en z is de hoogte gemeten in de richting van de zwaartekracht.
Het is impliciet in de vergelijking van Bernoulli dat de energie van een vloeistof uit drie componenten bestaat:
- Een kinetische component, die het resultaat is van de snelheid waarmee de vloeistof beweegt.
- Een potentiële of zwaartekrachtcomponent, die te wijten is aan de hoogte waarop de vloeistof zich bevindt.
- Een drukenergie, dat is de energie die het fluïdum bezit als gevolg van de druk waaraan het wordt blootgesteld.
Aan de andere kant kan de vergelijking van Bernoulli ook als volgt worden uitgedrukt:
v1 twee ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vtweetwee ∙ ƿ / 2 + Ptwee + ƿ ∙ g ∙ ztwee
Deze laatste uitdrukking is erg praktisch om de veranderingen te analyseren die een vloeistof ervaart wanneer een van de elementen waaruit de vergelijking bestaat, verandert.
Vereenvoudigde vorm
Bij bepaalde gelegenheden is de verandering in de ρgz-term van de vergelijking van Bernoulli minimaal in vergelijking met die van de andere termen, dus het kan worden verwaarloosd. Dit gebeurt bijvoorbeeld bij stromingen die een vliegtuig tijdens de vlucht ervaart..

Bij deze gelegenheden wordt de vergelijking van Bernoulli als volgt uitgedrukt:
P + q = P0
In deze uitdrukking is q dynamische druk en is gelijk aan v twee ∙ ƿ / 2, en P0 is de zogenaamde totale druk en is de som van de statische druk P en de dynamische druk q.
Toepassingen

De stelling van Bernoulli heeft veel en diverse toepassingen op gebieden die zo divers zijn als wetenschap, techniek, sport, enz..
Een interessante toepassing is te vinden in het ontwerp van open haarden. De schoorstenen zijn hoog gebouwd om een groter drukverschil tussen de basis en de schoorsteenuitlaat te bereiken, waardoor het gemakkelijker is om de verbrandingsgassen af te voeren.
De vergelijking van Bernoulli is natuurlijk ook van toepassing op de studie van de beweging van vloeistofstromen in leidingen. Uit de vergelijking volgt dat een verkleining van de dwarsdoorsnede van de buis, om de snelheid van het fluïdum dat er doorheen gaat te verhogen, ook een afname van de druk impliceert..
De Bernoulli-vergelijking wordt ook gebruikt in de luchtvaart en in Formule 1-voertuigen. In het geval van de luchtvaart is het Bernoulli-effect de oorsprong van de lift van vliegtuigen.
Vliegtuigvleugels zijn ontworpen met als doel een grotere luchtstroom aan de bovenkant van de vleugel te bereiken.
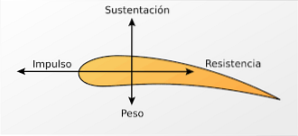
Dus in het bovenste deel van de vleugel is de luchtsnelheid hoog en daarom is de druk lager. Dit drukverschil produceert een verticaal opwaarts gerichte kracht (liftkracht) waardoor het vliegtuig in de lucht kan zweven. Een soortgelijk effect wordt verkregen in de rolroeren van Formule 1-auto's.
Oefening opgelost
Door een pijp met een doorsnede van 4,2 cmtwee een waterstroom stroomt met 5,18 m / s. Het water daalt van een hoogte van 9,66 m naar een lager niveau met een hoogte van nul elevatie, terwijl de doorsnede van de buis toeneemt tot 7,6 cmtwee.
a) Bereken de snelheid van de waterstroom op het lagere niveau.
b) Bepaal de druk op het onderste niveau in de wetenschap dat de druk op het bovenste niveau 152.000 Pa is.
Oplossing
a) Gezien het feit dat de stroming behouden moet blijven, is het waar dat:
QHoogste niveau = Qlager niveau
v1 . S1 = vtwee . Stwee
5,18 m / s. 4,2 cmtwee = vtwee . 7,6 cm ^twee
Oplossend voor, wordt verkregen dat:
vtwee 2,86 m / s
b) Toepassen van de stelling van Bernoulli tussen de twee niveaus, en rekening houdend met het feit dat de dichtheid van water 1000 kg / m is3 , er wordt verkregen dat:
v1 twee ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vtweetwee ∙ ƿ / 2 + Ptwee + ƿ ∙ g ∙ ztwee
(1/2). 1000 kg / m3 . (5,18 m / s)twee + 152000 + 1000 kg / m3 . 10 m / stwee . 9,66 m =
= (1/2). 1000 kg / m3 . (2,86 m / s)twee + P.twee + 1000 kg / m3 . 10 m / stwee . 0 m
Oplossen voor Ptwee jij mag:
P.twee = 257926,4 Pa
Referenties
- Bernoulli's principe. (n.d.). Op Wikipedia. Opgehaald op 12 mei 2018, via es.wikipedia.org.
- Bernoulli's principe. (n.d.). Op Wikipedia. Opgehaald op 12 mei 2018, via en.wikipedia.org.
- Batchelor, G.K. (1967). Een inleiding tot vloeistofdynamica. Cambridge University Press.
- Lam, H. (1993). Hydrodynamica (6e ed.). Cambridge University Press.
- Mott, Robert (1996). Toegepaste vloeistofmechanica (4e ed.). Mexico: Pearson Education.


Niemand heeft nog op dit artikel gereageerd.