
De stellingbeschrijving, toepassingen, voorbeelden en oefeningen van Norton
De De stelling van Norton, die wordt toegepast op elektrische circuits, stelt vast dat een lineair circuit met twee aansluitingen a en b kan worden vervangen door een volledig gelijkwaardige, die bestaat uit een stroombron genaamd INiet parallel geschakeld met een weerstand RNiet.
Zei huidige INiet ik vernamN Het is degene die tussen de punten a en b zou stromen als ze zouden worden kortgesloten. De weerstand RN is de equivalente weerstand tussen de aansluitingen, wanneer alle onafhankelijke bronnen worden uitgeschakeld. Alles wat gezegd is, wordt geschetst in figuur 1.

De zwarte doos in de figuur bevat het lineaire circuit dat moet worden vervangen door zijn Norton-equivalent. Een lineaire schakeling is er een waarin de ingang en de uitgang een lineaire afhankelijkheid hebben, zoals de relatie tussen de spanning V en de gelijkstroom I in een ohms element: V = I.R.
Deze uitdrukking komt overeen met de wet van Ohm, waarbij R de weerstand is, die ook een impedantie kan zijn, als het een wisselstroomcircuit is.
De stelling van Norton is ontwikkeld door de elektrotechnisch ingenieur en uitvinder Edward L. Norton (1898-1983), die lange tijd voor Bell Labs heeft gewerkt..
Artikel index
- 1 Toepassingen van de stelling van Norton
- 1.1 Verband tussen de stellingen van Norton en Thevenin
- 2 Voorbeeld
- 3 Oefening opgelost
- 4 referenties
Toepassingen van de stelling van Norton
Als je zeer gecompliceerde netwerken hebt, met veel weerstanden of impedanties en je wilt de spanning tussen elk ervan berekenen, of de stroom die er doorheen stroomt, dan vereenvoudigt de stelling van Norton de berekeningen, aangezien zoals we hebben gezien, het netwerk kan worden vervangen door een kleiner en beter beheersbaar circuit.
Op deze manier is de stelling van Norton erg belangrijk bij het ontwerpen van circuits met meerdere elementen, en om hun reactie te bestuderen..
Verband tussen de stellingen van Norton en Thevenin
De stelling van Norton is de tweeledige stelling van Thevenin, wat betekent dat ze equivalent zijn. De stelling van Thevenin geeft aan dat de zwarte doos in figuur 1 kan worden vervangen door een spanningsbron in serie met een weerstand, de Thevenin-weerstand R genoemdTh. Dit komt tot uiting in de volgende figuur:
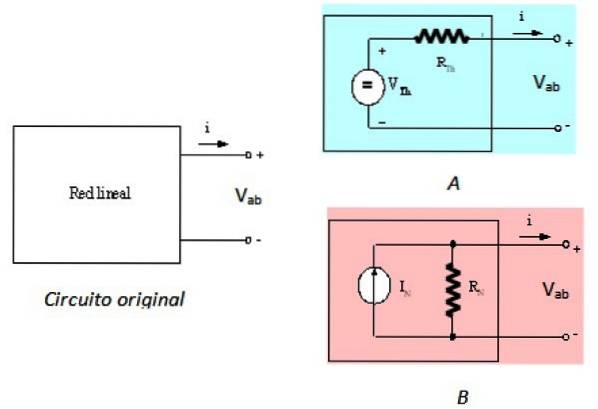
Het circuit aan de linkerkant is het originele circuit, het lineaire netwerk in de zwarte doos, circuit A rechtsboven is het Thevenin-equivalent en het circuit B het is het Norton-equivalent, zoals beschreven. Gezien vanaf de terminals a en b, zijn de drie circuits equivalent.
Merk nu op dat:
-In het oorspronkelijke circuit is de spanning tussen de klemmen Vab.
-V.ab = VTh in het circuit NAAR
-Ten slotte Vab = IkN.RN in het circuit B
Als de klemmen a en b in alle drie de circuits worden kortgesloten, moet ervoor worden gezorgd dat de spanning en stroom tussen deze punten voor alle drie hetzelfde moeten zijn, aangezien ze equivalent zijn. Dan:
-In het oorspronkelijke circuit is de stroom i.
-Voor circuit A is de stroom i = VTh / RTh, volgens de wet van Ohm.
-Ten slotte is in circuit B de stroom IN
Daarom wordt geconcludeerd dat de Norton- en Thevenin-weerstanden dezelfde waarde hebben, en dat de stroom wordt gegeven door:
ik = ikN = VTh / RTh = VTh / RN
Voorbeeld
Om de stelling van Norton correct toe te passen, worden de volgende stappen gevolgd:
-Isoleer van het netwerk het gedeelte van het circuit waarvoor het Norton-equivalent te vinden is.
-Geef in het overige circuit de klemmen a en b aan.
-Vervang de spanningsbronnen voor kortsluiting en de stroombronnen voor open circuits om de equivalente weerstand tussen klemmen a en b te vinden. Dit is RN.
-Breng alle bronnen terug naar hun oorspronkelijke posities, sluit klemmen a en b kort, en zoek de stroom die ertussen vloeit. Dit ben ikN.
-Teken het Norton-equivalentcircuit volgens wat is aangegeven in figuur 1. Zowel de stroombron als de equivalente weerstand zijn parallel.
Je kunt ook de stelling van Thevenin toepassen om R te vindenTh, waarvan we al weten is gelijk aan RN, dan kun je volgens de wet van Ohm I vindenN en ga verder met het tekenen van het resulterende circuit.
En laten we nu een voorbeeld bekijken:
Zoek het Norton-equivalent tussen de punten A en B van het volgende circuit:
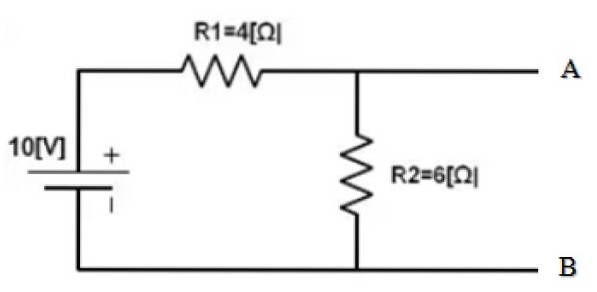
Het deel van de schakeling waarvan het equivalent te vinden is, is al geïsoleerd. En de punten A en B zijn duidelijk bepaald. Het volgende is om de 10 V-bron kort te sluiten en de equivalente weerstand van het verkregen circuit te vinden:
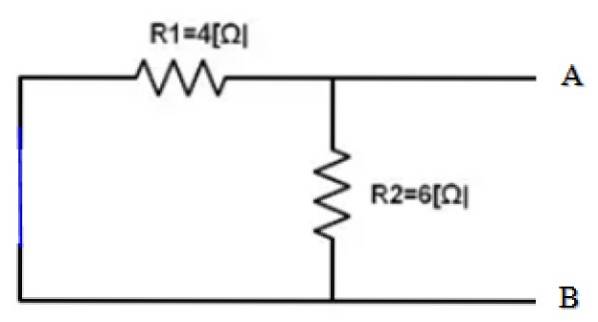
Uitzicht vanaf terminals A en B, beide weerstanden R1 en Rtwee zijn parallel, daarom:
1 / R.eq = 1 / R12 = (1/4) + (1/6) Ω-1 = 5/12 Ω-1 → R.eq = 12/5 Ω = 2,4 Ω
Vervolgens wordt de bron teruggebracht naar zijn plaats en worden de punten A en B kortgesloten om de stroom te vinden die daar circuleert, dit zal ik zijnN. In dat geval:
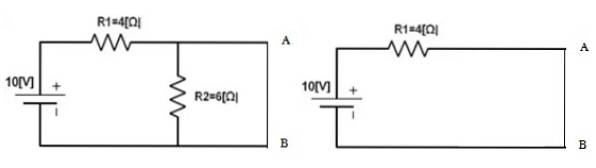
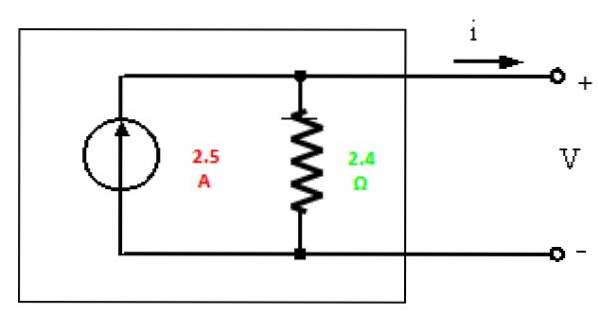
ikN = 10 V / 4 Ω = 2,5 A
Norton-equivalent
Ten slotte wordt het Norton-equivalent getekend met de gevonden waarden:
Oefening opgelost
In het circuit van de volgende afbeelding:
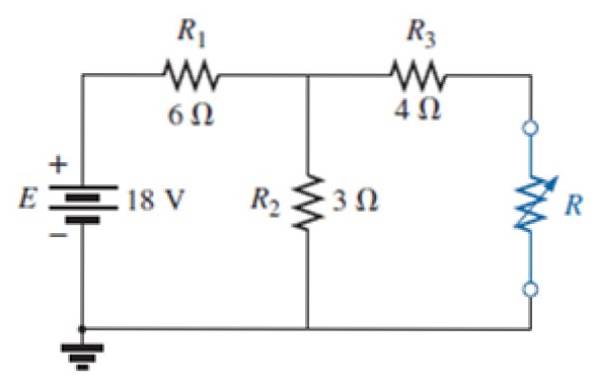
a) Zoek het Norton-equivalentcircuit van het externe netwerk naar de blauwe weerstand.
b) Vind ook het Thévenin-equivalent.
Oplossing voor
Door de bovenstaande stappen te volgen, moet de bron worden kortgesloten:
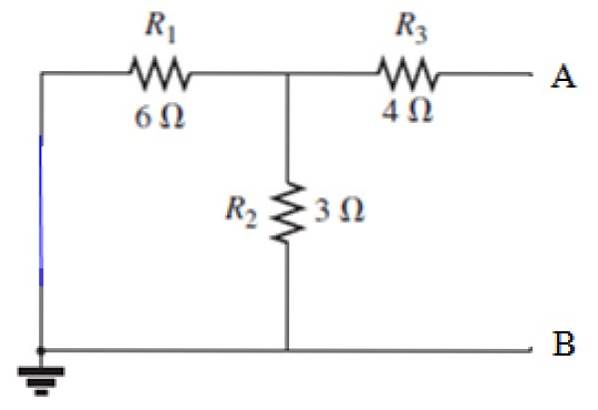
Berekening van RN
Uitzicht vanaf klemmen A en B, weerstand R3 staat in serie met de parallel gevormd door weerstanden R1 en Rtwee, laten we eerst de equivalente weerstand van deze parallel berekenen:
1 / R.12 = (1/6) + (1/3) Ω-1 = 1/2 Ω-1 → R.eq = 2/1 Ω = 2 Ω
En dan is deze parallel in serie met R3, zodat de equivalente weerstand is:
Req = 2 Ω + 4 Ω = 6 Ω
Dit is de waarde van beide RN vanaf RTh, zoals eerder uitgelegd.
IN berekening
De klemmen A en B worden dan kortgesloten, waardoor de bron op zijn plaats terugkeert:
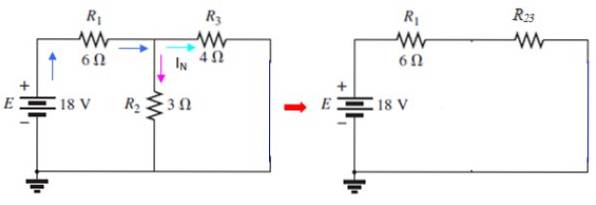
De stroom door ik3 is de huidige ikN gezocht, die kan worden bepaald met behulp van de mesh-methode of met behulp van series en parallel. In dit circuit Rtwee en R3 zijn parallel:
1 / R.2. 3 = (1/3) + (1/4) Ω-1 = 7/12 Ω-1 → R.2. 3 = 12/7 Ω
De weerstand R1 in serie staat met deze parallel, dan:
R123 = 6 + (12/7) Ω = 54/7 Ω
De stroom die de bron verlaat (blauwe kleur) wordt berekend met behulp van de wet van Ohm:
V = I. R → I = V / R = 18 V / (54/7 Ω) = 7/3 EEN
Deze stroom is verdeeld in twee delen: een die door R gaattwee en een andere die R kruist3. De stroom door parallel R2. 3 het is hetzelfde dat door R gaat1, zoals te zien in de tussenkring in de figuur. De spanning daar is:
V.2. 3 = I.R2. 3 = (7/3) A. (12/7) Ω = 4 V
Beide weerstanden Rtwee en R3 bevinden zich op die spanning, omdat ze parallel zijn, daarom:
ik3 = V2. 3 / R3 = 4 V / 4 Ω = 1 EEN
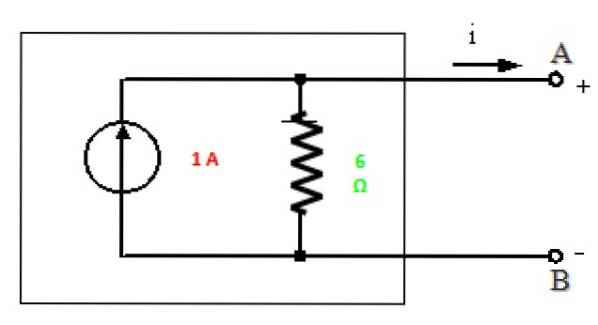
We hebben al de huidige Norton gezocht, aangezien ik zoals eerder al zei3 = IkN, dan:
ikN = 1 A
Norton-equivalent
Alles is klaar om het Norton-equivalent van dit circuit tussen punten A en B te tekenen:
Oplossing b
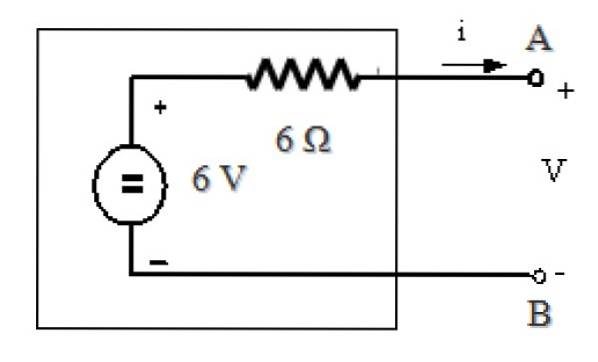
Het vinden van het Thévenin-equivalent is heel eenvoudig, aangezien RTh = RN= 6 Ω en zoals uitgelegd in de voorgaande secties:
V.Th = IkN. RN = 1 A. 6 Ω = 6 V
Het equivalentcircuit van Thévenin is:
Referenties
- Alexander, C. 2006. Grondbeginselen van elektrische schakelingen. 3e. Editie. Mc Graw Hill.
- Boylestad, R. 2011. Inleiding tot circuitanalyse. 2e. Editie. Pearson.
- Dorf, R. 2006. Inleiding tot elektrische schakelingen. 7e. Editie. John Wiley & Sons.
- Edminister, J. 1996. Electrical Circuits. Schaum-serie. 3e. Editie. Mc Graw Hill.
- Wikipedia. De stelling van Norton. Hersteld van: es.wikipedia.org.



Niemand heeft nog op dit artikel gereageerd.