
De stelling van Thévenin waaruit het bestaat, toepassingen en voorbeelden
De De stelling van Thévenin stelt dat een circuit met aansluitingen A en B kan worden vervangen door een equivalent bestaande uit een bron en een serieweerstand, waarvan de waarden hetzelfde potentiaalverschil geven tussen A en B en dezelfde impedantie als het originele circuit.
Deze stelling werd in 1883 bekendgemaakt door de Franse ingenieur Léon Charles Thévenin, maar er wordt beweerd dat hij dertig jaar eerder werd verkondigd door de Duitse natuurkundige Hermann von Helmholtz..

Het nut ervan ligt in het feit dat, zelfs wanneer het originele circuit complex of onbekend is, voor de doeleinden van een belasting of impedantie die tussen de klemmen A en B wordt geplaatst, het eenvoudige Thévenin-equivalentcircuit zich op dezelfde manier gedraagt als het origineel..
Artikel index
- 1 Hoe bereken je stap voor stap de equivalente spanning?
- 1.1 - Experimenteel
- 1.2 - Het circuit oplossen
- 2 Toepassingen van de stelling van Thévenin (deel I)
- 2.1 Voorbeeld 1a (berekening van de equivalente spanning stap voor stap)
- 2.2 Voorbeeld 1b (stroom in de belasting met het Thévenin-equivalent)
- 3 Bewijs van de stelling van Thévenin
- 4 Toepassing van de stelling van Thévenin (deel II)
- 4.1 Voorbeeld 2a (Thévenin-equivalente weerstand)
- 4.2 Voorbeeld 2b
- 4.3 Voorbeeld 2c
- 5 Toepassing van de stelling van Thévenin (deel III)
- 5.1 Voorbeeld 3
- 6 referenties
Hoe bereken je stap voor stap de equivalente spanning?
Het spannings- of potentiaalverschil van het equivalente circuit kan op de volgende manieren worden verkregen:
- Experimenteel
Het verkrijgen van de equivalente Thévenin-spanning
Als het een apparaat of uitrusting is die zich in een "zwarte doos" bevindt, wordt het potentiaalverschil tussen klemmen A en B gemeten met een voltmeter of een oscilloscoop. Het is erg belangrijk dat er geen belasting of impedantie wordt geplaatst tussen klemmen A en B..
Een voltmeter of een oscilloscoop vertegenwoordigt geen enkele belasting op de klemmen, aangezien beide apparaten een zeer grote impedantie hebben (idealiter oneindig) en het zou zijn alsof klemmen A en B zonder belasting zouden zijn. De spanning of spanning die op deze manier wordt verkregen, is de Thévenin-equivalente spanning.
Het verkrijgen van de Thévenin-equivalente impedantie
Om de equivalente impedantie uit een experimentele meting te verkrijgen, wordt een bekende weerstand geplaatst tussen klemmen A en B en wordt de spanningsval of het spanningssignaal gemeten met een oscilloscoop..
Uit de spanningsval in de bekende weerstand tussen de klemmen kan de stroom die erdoor vloeit worden verkregen.
Het product van de verkregen stroom met de equivalente weerstand plus de spanningsval gemeten in de bekende weerstand is gelijk aan de equivalente Thévenin-spanning die eerder werd verkregen. Uit deze gelijkheid wordt de equivalente Thévenin-impedantie gewist.
- Het circuit oplossen
Berekening van de Thévenin-equivalente spanning
Ten eerste wordt elke belasting of impedantie losgekoppeld van klemmen A en B..
Zoals het circuit bekend is, worden mesh-theorie of de wetten van Kirchhoff toegepast om de spanning op de klemmen te vinden. Deze spanning zal het equivalent zijn van Thévenin.
Berekening van de Thévenin-equivalente impedantie
Om de equivalente impedantie te verkrijgen, gaan we verder met:
- Vervang de spanningsbronnen van het originele circuit door kortsluiting "nul impedantie" en de stroombronnen van het originele circuit door open "oneindige impedantie".
- Vervolgens wordt de equivalente impedantie berekend volgens de regels van serie-impedanties en parallelle impedanties.
Toepassingen van de stelling van Thévenin (deel I)
We zullen de stelling van Thévenin toepassen om enkele circuits op te lossen. In dit eerste deel beschouwen we een circuit dat alleen spanningsbronnen en weerstanden heeft.
Voorbeeld 1a (berekening van equivalente spanning stap voor stap)
Figuur 2 toont het circuit dat zich in een hemelkast bevindt met twee elektromotorische krachtbatterijen V1 en V2 respectievelijk en weerstanden R1 en R2, het circuit heeft klemmen A en B waarop een belasting kan worden aangesloten.
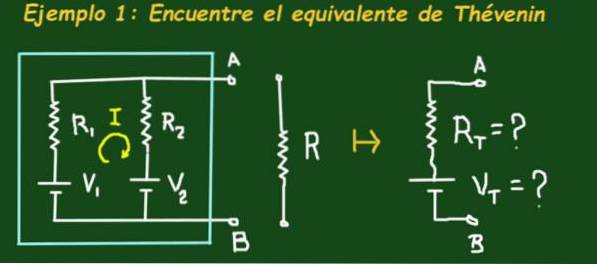
Het doel is om het Thévenin-equivalentcircuit te vinden, dat wil zeggen om de Vt- en Rt-waarden van het equivalente circuit te bepalen. Pas de volgende waarden toe: V1 = 4V, V2 = 1V, R1 = 3Ω, R2 = 6Ω en R = 1Ω.
Stap voor stap oplossing
Stap 1
We bepalen de spanning op de klemmen A en B als er geen belasting op staat.
Stap 2
Het op te lossen circuit bestaat uit een enkele mesh waardoor een stroom I circuleert die we positief hebben genomen met de klok mee.
Stap 3
We gaan door het gaas, beginnend met de linker benedenhoek. Het pad leidt tot de volgende vergelijking:
V1 - I * R1 - I * R2 - V2 = 0
Stap 4
We lossen de maasstroom I op en verkrijgen:
I = (V1 -V2) / (R1 + R2) = (4V - 1V) / (3Ω + 6Ω) = ⅓ EEN
Stap 5
Met de maasstroom kunnen we het spanningsverschil tussen A en B bepalen, dat is:
Vab = V1 - I * R1 = 4V - ⅓ EEN * 3Ω = 3V
Dat wil zeggen, de Thevenin-equivalente spanning is: Vt = 3V.
Stap 6 (Thévenin-equivalente weerstand)
We gaan nu verder met het berekenen van de Thévenin-equivalente weerstand, waarvoor en zoals eerder vermeld, de spanningsbronnen worden vervangen door een kabel.
In dat geval hebben we maar twee weerstanden parallel, dus de Thévenin-equivalente weerstand is:
Rt = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω
Voorbeeld 1b (stroom in de belasting met het Thévenin-equivalent)
Verbind als een belasting met klemmen A en B een weerstand R = 1Ω naar het equivalente circuit en vind de stroom die door de belasting vloeit.
Oplossing
Wanneer de weerstand R is verbonden met het Thevenin-equivalentcircuit, hebben we een eenvoudig circuit dat bestaat uit een bron Vt een weerstand Rt in serie met de weerstand R.
We noemen Ic de stroom die door de belasting R stroomt, zodat de mesh-vergelijking er als volgt uitziet:
Vt - Ic * Rt - Ic * R = 0
waaruit volgt dat Ic wordt gegeven door:
Ic = Vt / (Rt + R) = 3V / (2Ω + 1Ω) = 1 EEN
Bewijs van de stelling van Thévenin
Om te verifiëren dat de stelling van Thévenin klopt, verbindt u R met het oorspronkelijke circuit en vindt u de stroom die door R vloeit door de mesh-wet toe te passen op het resulterende circuit.
Het resulterende circuit blijft bestaan en de mesh-vergelijkingen blijven zoals weergegeven in de volgende afbeelding:
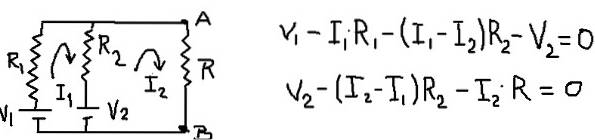
Door de mesh-vergelijkingen toe te voegen, is het mogelijk om de mesh-stroom I1 te vinden als functie van de huidige I2. Vervolgens wordt het vervangen door de tweede mesh-vergelijking en blijft er een vergelijking over met I2 als de enige onbekende. De volgende tabel toont de bewerkingen.
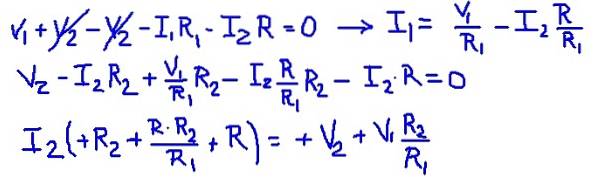
Vervolgens worden de waarden van de weerstand en spanningen van de bronnen vervangen, waardoor de numerieke waarde van de maasstroom I2 wordt verkregen.

De maasstroom I2 is de stroom die door de belastingsweerstand R vloeit en de gevonden waarde van 1 A komt volledig overeen met die eerder gevonden met het equivalente Thévenin-circuit..
Toepassing van de stelling van Thévenin (deel II)
In dit tweede deel zal de stelling van Thévenin worden toegepast in een circuit met spanningsbronnen, stroombronnen en weerstanden.
Voorbeeld 2a (Thévenin-equivalente weerstand)
Het doel is om het Thévenin-equivalentcircuit te bepalen dat overeenkomt met het circuit in de volgende afbeelding, wanneer de aansluitingen geen weerstand van 1 ohm hebben, wordt de weerstand geplaatst en wordt de stroom die erdoor circuleert bepaald.
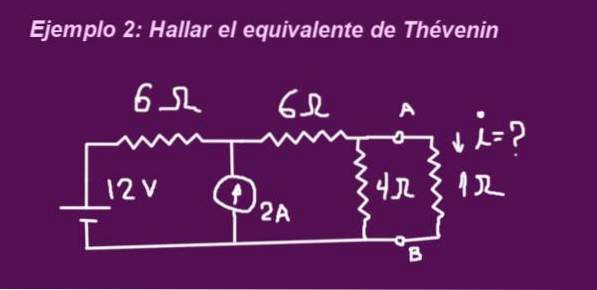
Oplossing
Om de equivalente weerstand te vinden, verwijdert u de belastingsweerstand (in dit geval de 1 ohm). Ook worden spanningsbronnen vervangen door een kortsluiting en stroombronnen door een open circuit..
Op deze manier is het circuit waarvoor de equivalente weerstand wordt berekend, het circuit dat hieronder wordt weergegeven:
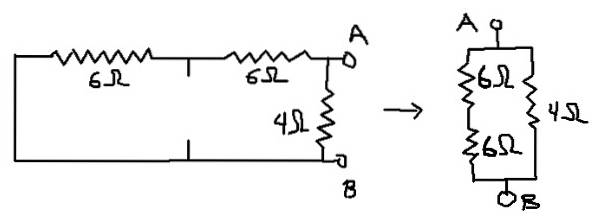
Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω wat de Thevenin-equivalente weerstand (Rth) is.
Voorbeeld 2b
Bereken de Thévenin-equivalente spanning.
Oplossing
Om de Thévenin-equivalente spanning te berekenen, beschouwen we het volgende circuit, waarin we de stromen in de I1 en I2 plaatsen in de takken die worden aangegeven in de volgende afbeelding:
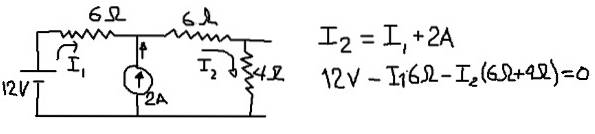
De vorige afbeelding toont de vergelijking van de huidige knooppunten en de vergelijking van spanningen wanneer de externe mesh wordt doorlopen. Vanaf de tweede van de vergelijkingen wordt de huidige I1 gewist:
I1 = 2 - I2 * (5/3)
Deze vergelijking wordt vervangen in de vergelijking van de knooppunten:
I2 = 2 - (5/3) I2 + 2 ===> I2 (8/3) = 4 ===> I2 = 12/8 = 1,5 A
Dit betekent dat de spanningsval over de weerstand van 4 ohm 6 volt is..
Kortom, de Thévenin-spanning is Vth = 6 V..
Voorbeeld 2c
Het vinden van het Thevenin-equivalente circuit en de stroom in de belastingsweerstand.
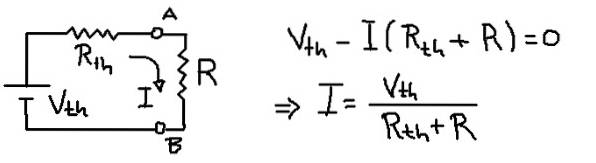
Oplossing
De vorige afbeelding toont het Thévenin-equivalentcircuit met de belastingsweerstand R.Uit de spanningsvergelijking in de mesh wordt de stroom I die door de belastingsweerstand R stroomt afgeleid.
Ik = Vth / (Rth + R) = 6V / (3Ω + 1Ω) = 1,5 EEN
Toepassing van de stelling van Thévenin (deel III)
In dit derde deel van de toepassing van de stelling van Thévenin wordt een wisselstroomcircuit beschouwd dat een wisselspanningsbron, een condensator, een inductantie en een weerstand bevat..
Voorbeeld 3
Het doel is om het Thévenin Circuit te vinden dat gelijkwaardig is aan het volgende circuit:
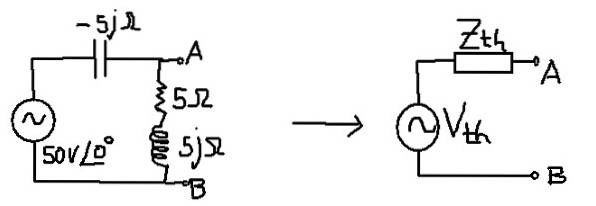
Oplossing
De equivalente impedantie komt overeen met die van de condensator parallel aan de seriecombinatie van de weerstand en inductie.
De inverse van de equivalente impedantie wordt gegeven door:
Zeq ^ -1 = (-5j) ^ - 1 + (5 + 5j) ^ - 1 = (1/5) j + ((1/10 + (1/10) j) = (1/10 + 3 / 10 j) Mho
En de equivalente impedantie zal dan zijn:
Zeq = (1 - 3 j) Ohm
De complexe stroom I kan worden afgeleid uit de mesh-vergelijking:
50V∠0 - I (-5 j + 5 + 5j) = 50V∠0 - I * 5 = 0 ===> I = 10A ∠0
Nu wordt de spanningsval in de weerstand plus de inductantie berekend, dat wil zeggen de spanning Vab die de equivalente Thévenin-spanning zal zijn:
Vab = I * (5 + 5 j) Ω = 10A ∠0 * 5Ω∠45º = 50V∠45º
Met andere woorden, de equivalente spanning heeft dezelfde piekwaarde als de originele bron, maar is 45 graden uit fase: Vth = 50V∠45º
Referenties
- Elektronica-tutorials, de stelling van Thevenin. Hersteld van: electronics-tutorials.ws
- Netwerktheorie vragen en antwoorden. De stelling van Thevenin. Hersteld van: sanfoundry.com
- De stelling van Thevenin. Stap voor stap procedure. Hersteld van: electrictechnology.org
- De stelling van Thevenin. Opgelost voorbeeld stap voor stap. Hersteld van: electricalsimple.blogspot.com
- Workshop over de stellingen van Thevenin en Norton. Hersteld van: web.iit.edu
- Wikipedia. De stelling van Thévenin. Hersteld van: wikipedia.com


Niemand heeft nog op dit artikel gereageerd.