De horizontaal schot Het is de lancering van een projectiel met horizontale snelheid vanaf een bepaalde hoogte en overgelaten aan de werking van de zwaartekracht. Zonder rekening te houden met de luchtweerstand, zal het pad beschreven door de mobiel de vorm hebben van een paraboolboog.
Het is vrij gebruikelijk om objecten horizontaal te projecteren. De projectielen worden voor allerlei doeleinden afgevuurd: van de stenen waarmee de dammen aan het begin van het verhaal werden geraakt, tot die bij balsporten en op de voet gevolgd door menigten.
Artikel index
De belangrijkste kenmerken van de horizontale opname zijn:
-De beginsnelheid die aan het projectiel wordt gegeven, staat loodrecht op de zwaartekracht.
-De beweging vindt plaats in een vlak, dus er zijn twee coördinaten nodig: X Y Y.
-Het wordt gedaan vanaf een bepaalde hoogte H boven het maaiveld.
-De tijd dat het projectiel in de lucht blijft, wordt genoemd vluchttijd.
-Factoren als luchtweerstand en fluctuaties in de waarde van g.
-De vorm, grootte en massa van het projectiel hebben geen invloed op de beweging ervan.
-De beweging valt uiteen in twee gelijktijdige bewegingen: een verticaal naar beneden onder invloed van gde andere, horizontaal, met constante snelheid.
De kinematische vergelijkingen voor horizontale lancering worden verkregen uit de vergelijkingen voor vrije val en die voor uniforme rechtlijnige beweging..
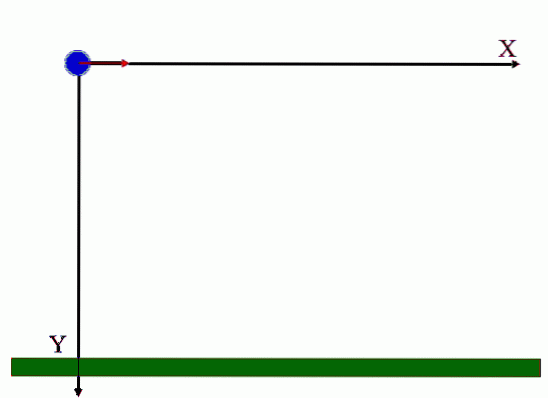
Zoals de animatie in figuur 1 duidelijk laat zien, krijgt het projectiel een horizontale beginsnelheid, aangeduid als vof = vos ik (vetgedrukt in gedrukte tekst geeft aan dat het een vector is).
Merk op dat de beginsnelheid een grootte heeft vos en is gericht langs de as X, wat is de richting van de eenheidsvector ik. De animatie laat ook zien dat de beginsnelheid geen verticale component heeft, maar naarmate deze daalt, neemt deze component gelijkmatig toe, dankzij de actie van g, zwaartekrachtversnelling.
Wat betreft de horizontale snelheidscomponent, deze blijft constant gedurende de beweging.
Volgens het voorgaande worden de posities bepaald in functie van de tijd, zowel op de horizontale as als op de verticale as. De richting naar rechts wordt genomen als de + x-as, terwijl de richting naar beneden de -y-richting is. De waarde van zwaartekracht is g = -9,8 m / stwee of -32 ft / stwee
x (t) = xof + vos.t (horizontale positie); vos het is constant
y (t) = yof + vHallo.t - ½ g.ttwee (verticale positie); vY = vHallo - g.t (verticale snelheid)
De vergelijkingen worden vereenvoudigd door de volgende startposities te kiezen: Xof = 0, Yof = 0 op de lanceerplaats. Bovendien vHallo = 0, aangezien de mobiel horizontaal wordt geprojecteerd. Met deze keuze zijn de bewegingsvergelijkingen als volgt:
x (t) = vos.t; vX = vos
y (t) = - ½ g.ttweevY = - g.t
Als er geen tijd beschikbaar is, is de vergelijking die betrekking heeft op snelheden en verplaatsingen nuttig. Dit geldt voor de verticale snelheid, aangezien de horizontaal tijdens de beweging constant blijft:
vYtwee = vHallotwee + 2.g .y = 2.g.y
Om de vliegtijd tvlucht, stel dat de mobiel van een hoogte wordt geprojecteerd H. op de vloer. Omdat de oorsprong van het referentiesysteem is gekozen op het startpunt, bevindt het zich in de positie wanneer het de grond bereikt -H.. Als we dit in vergelijking 2) vervangen, krijgen we:
-H = - ½ g.ttweevlucht
tvlucht = (2H / g)½
De horizontaal bereik wordt verkregen door deze tijd in te wisselen x (t)
Xmax. hoogte = vos. (2H / g)½
Een helikopter vliegt horizontaal en behoudt een constante hoogte van 580 m wanneer hij een doos met voedsel boven een vluchtelingenkamp laat vallen. De kist landt op een horizontale afstand van 150 m vanaf het punt van lancering. Zoek: a) De vliegtijd van de doos.
b) De snelheid van de helikopter.
c) Hoe snel raakte de doos de grond??
a) De hoogte H vanwaar het voedsel valt is H = 500 m. Met deze gegevens verkrijgen we bij vervanging:
tvlucht = (2H / g)½= (2 x 580 / 9,8) ½s = 10,9 s
b) De helikopter voert de aanvankelijke horizontale snelheid vos van het pakket en aangezien een van de gegevens is Xmax. hoogte
Xmax. hoogte = vos. (2H / g)½ vos = xmax. hoogte / (2H / g)½= xmax. hoogte / tvlucht = 150 m / 10,9 s = 13,8 m / s
c) De snelheid van het projectiel op elk moment is:
vY = -g.t = -9,8 m / stwee x 10,9 s = -106,82 m / s = - 384,6 km / uur
Het minteken geeft aan dat de gsm naar beneden beweegt.
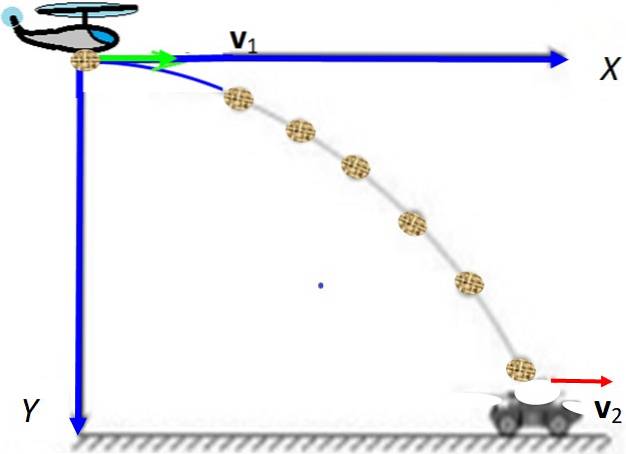
Vanuit een vliegtuig dat horizontaal op hoogte vliegt H = 500 m Y 200 km / u een pakket valt en moet vallen op een open voertuig dat in beweging is 18 km / u op de weg. In welke positie moet het vliegtuig het pakket laten vallen zodat het in het voertuig valt? Houd geen rekening met luchtweerstand of windsnelheid.
Het is handig om eerst alle eenheden door te geven aan het internationale systeem:
18 km / u = 6 m / s
200 km / u = 55 m / s
Er zijn twee mobiele telefoons: vliegtuig (1) en voertuig (2) en het is noodzakelijk om een coördinatensysteem te kiezen om ze beide te lokaliseren. Het is handig om het aan het beginpunt van het pakket in het vliegtuig te doen. Het pakket wordt horizontaal geprojecteerd met de snelheid die het vliegtuig draagt: v1, terwijl het voertuig rijdt vtwee aangenomen constant.
-Vliegtuig
Beginpositie: x = 0; y = 0
Initiële snelheid = v1 (horizontaal)
Positievergelijkingen: y (t) = -½g.ttwee x (t) = v1.t
-Voertuig
Beginpositie: x = 0, y = -H
Initiële snelheid = vtwee (constante)
x (t) = xof + vtwee. t
De duur van de vlucht van het pakket is:
tvlucht = (2H / g)½ (2 × 500 / 9,8)½s = 10,1 s
In deze tijd heeft het pakket een horizontale verplaatsing ondergaan van:
Xmax. hoogte = vos . (2H / g)½= 55 m / s x 10,1 s = 556 m.
In deze tijd heeft het voertuig zich ook horizontaal verplaatst:
x (t) = v1.t = 6 m / s x10,1 s = 60,6 m
Als het vliegtuig het pakket onmiddellijk laat vallen wanneer het het voertuig eronder ziet passeren, zal het er niet recht in vallen. Om dat te laten gebeuren, moet je het verder naar achteren gooien:
d = 556 m - 60,6 m = 495,4 m.
Niemand heeft nog op dit artikel gereageerd.