
Juiste trapezoïde eigenschappen, relaties en formules, voorbeelden
EEN rechthoek trapezium is een platte figuur met vier zijden, zodanig dat er twee evenwijdig aan elkaar staan, genoemd bases en ook een van de andere zijden staat loodrecht op de bases.
Om deze reden zijn twee van de interne hoeken juist, dat wil zeggen, ze meten 90 °. Vandaar de naam "rechthoek" die aan de figuur wordt gegeven. De volgende afbeelding van een rechter trapezium verduidelijkt deze kenmerken:
Artikel index
- 1 Elementen van de trapezium
- 2 Relaties en formules
- 2.1 Hoogte h van de trapezium
- 2.2 Omtrek P
- 2.3 Gemiddelde basis
- 2.4 Gebied
- 2.5 Diagonalen, zijkanten en hoeken
- 3 Voorbeelden van rechter trapezoïden
- 3.1 De trapezium als ontwerpelement
- 3.2 Trapeziumvormige golfgenerator
- 3.3 Bij numerieke berekening
- 3.4 Balk met trapeziumvormige belasting
- 3.5 Als educatief en leermiddel
- 4 Opgeloste oefeningen
- 4.1 - Oefening 1
- 4.2 - Oefening 2
- 5 referenties
Elementen van de trapezium
De elementen van de trapezium zijn:
-Basissen
-Hoekpunten
-Hoogte
-Interne hoeken
-Middelste basis
-Diagonalen
We gaan deze elementen uitdiepen met behulp van figuren 1 en 2:
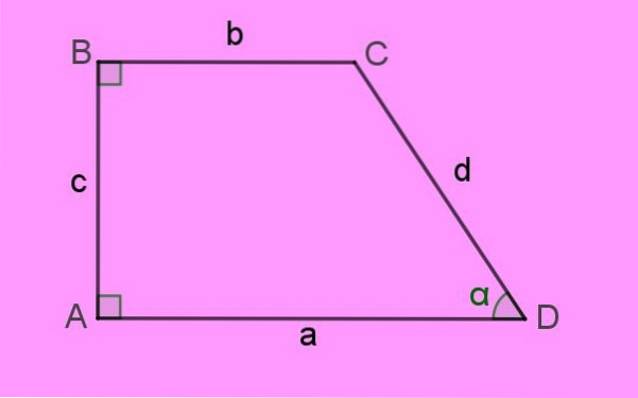
De zijkanten van de rechter trapezium worden aangeduid met kleine letters a, b, c en d. De hoeken van de figuur o hoekpunten Ze zijn aangegeven in hoofdletters. Eindelijk, de interne hoeken Ze worden uitgedrukt in Griekse letters.
Per definitie, bases van deze trapezium zijn de zijden a en b, die, zoals te zien is, evenwijdig zijn en ook verschillende lengtes hebben.
De zijde loodrecht op beide bases is de zijkant c naar links, dat is de hoogte h van de trapeze. En tenslotte is er de zijde d, die de scherpe hoek α vormt met de zijde a.
De som van de interne hoeken van een vierhoek is 360º. Het is gemakkelijk in te zien dat de ontbrekende hoek C in de figuur 180 - α is.
De middelste basis is het segment dat de middelpunten van de niet-parallelle zijden verbindt (segment EF in figuur 2).
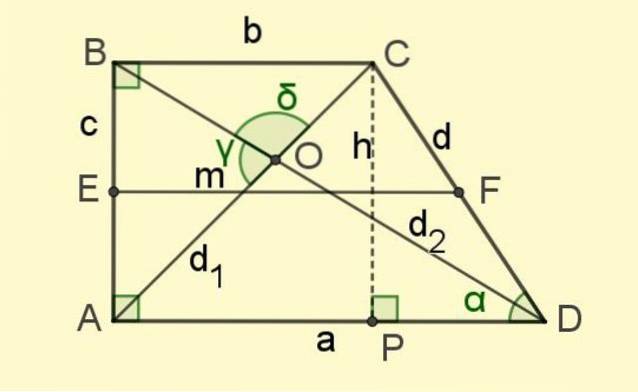
En als laatste zijn er de diagonalen d1 en dtwee, de segmenten die de tegenoverliggende hoekpunten samenvoegen en elkaar snijden in punt O (zie figuur 2).
Relaties en formules
Trapezium hoogte h
h = c
Omtrek P
Het is de maat van de contour en wordt berekend door de zijkanten op te tellen:
Omtrek = a + b + c + d
De kant d wordt uitgedrukt in termen van de hoogte of de zijkant c met behulp van de stelling van Pythagoras:
d = √ (a-b)twee + ctwee
Vervangen in de perimeter:
P = a + b + c + √ (a-b)twee + ctwee
Middelste basis
Het is de halve som van de basen:
Gemiddelde basis = (a + b) / 2
Soms wordt de gemiddelde basis op deze manier uitgedrukt:
Gemiddelde basis = (hoofdbasis + kleine basis) / 2
Oppervlakte
Het oppervlak A van de trapezium is het product van de gemiddelde basis maal de hoogte:
A = (Grote sokkel + kleine sokkel) x hoogte / 2
A = (a + b) c / 2
Diagonalen, zijkanten en hoeken
In figuur 2 verschijnen verschillende driehoeken, zowel rechts als niet-rechts. De stelling van Pythagoras kan worden toegepast op degenen die rechthoekige driehoeken zijn en op degenen die dat niet zijn, de cosinus- en sinusstellingen.
Op deze manier worden relaties gevonden tussen de zijkanten en tussen de zijkanten en interne hoeken van de trapezium..
CPA-driehoek
Het is een rechthoek, de poten zijn gelijk en zijn b waard, terwijl de hypotenusa de diagonaal d is1, Dus:
d1twee = btwee + btwee = 2btwee
DAB-driehoek
Het is ook een rechthoek, de poten zijn naar Y c (of ook naar Y h) en de hypotenusa is dtwee, zodat:
dtweetwee = eentwee + ctwee = eentwee + htwee
CDA-driehoek
Aangezien deze driehoek geen rechthoekige driehoek is, wordt hierop de cosinusstelling toegepast, of ook de sinusstelling.
Volgens de cosinusstelling:
d1twee = eentwee + dtwee - 2ad cos α
CDP-driehoek
Deze driehoek is een rechthoekige driehoek en met zijn zijden zijn de trigonometrische verhoudingen van de hoek α geconstrueerd:
zonde α = h / d
cos α = PD / d
Maar de zijkant PD = a - b, dus:
cos α = (a-b) / d → a - b = d cos α
een = b + d cos α
Je hebt ook:
tg α = sin α / cos α = h / (a-b) → h = tg α (a-b)
CBD driehoek
In deze driehoek hebben we de hoek waarvan het hoekpunt bij C is. Het is niet gemarkeerd in de figuur, maar aan het begin werd benadrukt dat het 180 - α is. Deze driehoek is geen rechthoekige driehoek, dus de cosinusstelling of sinusstelling kan worden toegepast..
Nu kan gemakkelijk worden aangetoond dat:
sin (180 - α) = sin α
cos (180 - α) = - cos α
De cosinusstelling toepassen:
dtweetwee = dtwee + btwee - 2db cos (180 - α) = dtwee + btwee + 2db cos α
Voorbeelden van rechter trapezoïden
Trapezoïden en in het bijzonder rechtertrapezoïden komen aan veel kanten voor, en soms niet altijd in tastbare vorm. Hier hebben we verschillende voorbeelden:
Het trapezium als designelement
Geometrische figuren zijn rijk aan de architectuur van veel gebouwen, zoals deze kerk in New York, die een structuur toont in de vorm van een rechthoekige trapezium.
Evenzo komt de trapeziumvorm vaak voor bij het ontwerp van containers, containers, bladen (snijder of exact), badges en in grafisch ontwerp.

Trapeziumvormige golfgenerator
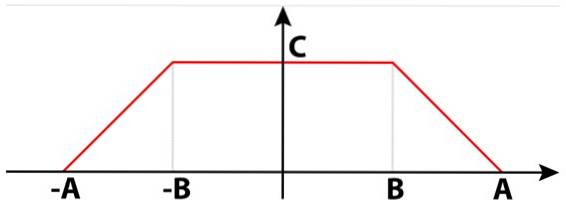
Elektrische signalen kunnen niet alleen vierkant, sinusvormig of driehoekig zijn. Er zijn ook trapeziumvormige signalen die in veel circuits nuttig zijn. In figuur 4 is er een trapeziumvormig signaal dat is samengesteld uit twee rechter trapezoïden. Tussen hen vormen ze een enkele gelijkbenige trapezium.
Bij numerieke berekening
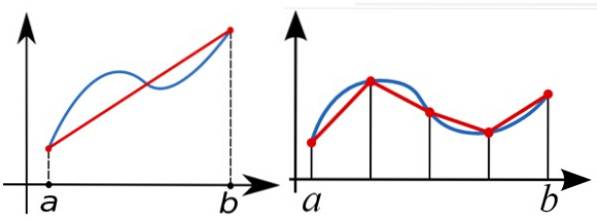
Om de definitieve integraal van de functie f (x) tussen a en b numeriek te berekenen, wordt de trapeziumregel gebruikt om het gebied onder de grafiek van f (x) te benaderen. In de volgende afbeelding wordt aan de linkerkant de integraal benaderd met een enkele rechter trapezium.
Een betere benadering is die in de rechter figuur, met meerdere rechter trapeziums.
Trapeziumvormige belaste balk
Krachten zijn niet altijd geconcentreerd op een enkel punt, aangezien de lichamen waarop ze werken aanzienlijke afmetingen hebben. Dat is het geval bij een brug waarover continu voertuigen circuleren, het water van een zwembad op de verticale wanden daarvan of een dak waarop water of sneeuw zich ophoopt..
Om deze reden worden krachten verdeeld per lengte-eenheid, oppervlakte of volume, afhankelijk van het lichaam waarop ze inwerken..
In het geval van een ligger kan een kracht verdeeld per lengte-eenheid verschillende verdelingen hebben, bijvoorbeeld de rechter trapezium die hieronder wordt weergegeven:
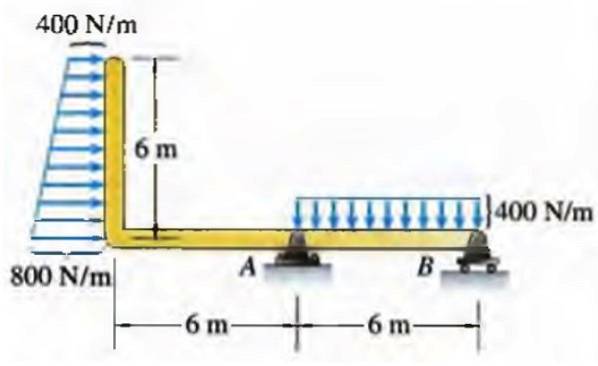
In werkelijkheid komen verdelingen niet altijd overeen met reguliere geometrische vormen zoals deze, maar ze kunnen in veel gevallen een goede benadering zijn..
Als educatief en leermiddel
Blokken en afbeeldingen met geometrische vormen, inclusief trapeziums, zijn erg handig voor kinderen om vanaf jonge leeftijd vertrouwd te raken met de fascinerende wereld van geometrie.

Opgeloste oefeningen
- Oefening 1
In de rechter trapezium in figuur 1 is de grotere basis 50 cm en de kleinere basis gelijk aan 30 cm, ook is bekend dat de schuine zijde 35 cm is. Vind:
a) Hoek α
b) Hoogte
c) Omtrek
d) Gemiddelde basis
e) Gebied
f) Diagonalen
Oplossing voor
De afschriftgegevens worden als volgt samengevat:
a = grote basis = 50 cm
b = kleinere basis = 30 cm
d = schuine zijde = 35 cm
Om de hoek α te vinden, bezoeken we het gedeelte met formules en vergelijkingen om te zien welke het beste past bij de verstrekte gegevens. De gezochte hoek wordt gevonden in verschillende van de geanalyseerde driehoeken, bijvoorbeeld het CDP.
Daar hebben we deze formule, die het onbekende bevat en ook de gegevens die we kennen:
cos α = (a-b) / d
Daarom:
α = bogen [(a-b) / d] = bogen [(50-30) / 35] = bogen 20/35 = 55,15 º
Oplossing b
Uit de vergelijking:
zonde α = h / d
Het wist h:
h = d. sin α = 35 zonde 55,15 º cm = 28,72 cm
Oplossing c
De omtrek is de som van de zijden, en aangezien de hoogte gelijk is aan zijde c, hebben we:
c = h = 28,72 cm
Daarom:
P = (50 + 30 + 35 + 28,72) cm = 143,72 cm
Oplossing d
De gemiddelde basis is de halve som van de basen:
Middenvoet = (50 + 30 cm) / 2 = 40 cm
Oplossing e
De oppervlakte van de trapezium is:
A = gemiddelde basis x hoogte = 40 cm x 28,72 = 1148,8 cmtwee.
Oplossing f
Voor de diagonaal d1 je kunt deze formule gebruiken:
d1twee = btwee + btwee = 2btwee
d1twee= 2 x (30 cm)twee = 1800 cmtwee
d1 = √1800 cmtwee = 42,42 cm
En voor de diagonaal dtwee
dtweetwee = dtwee + btwee + 2db cos α = (35 cm)twee + (30 cm)twee + 2 x 35 x 30 cmtwee cos 55,15 º = 3325 cmtwee
dtwee = √ 3325 cmtwee = 57,66 cm
Dit is niet de enige manier om d te vindentwee, aangezien er ook de DAB-driehoek is.
- Oefening 2
De volgende grafiek van snelheid als functie van de tijd behoort tot een mobiel die een gelijkmatig versnelde rechtlijnige beweging heeft. Bereken de afstand die de gsm aflegt tijdens het tijdsinterval tussen 0,5 en 1,2 seconden.
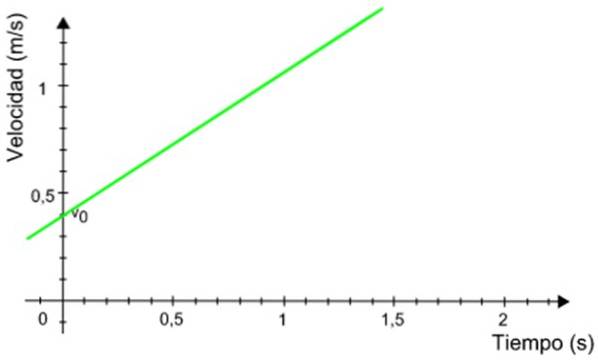
Oplossing
De afstand die de mobiele telefoon aflegt, is numeriek equivalent aan het gebied onder de grafiek, begrensd door het aangegeven tijdsinterval.
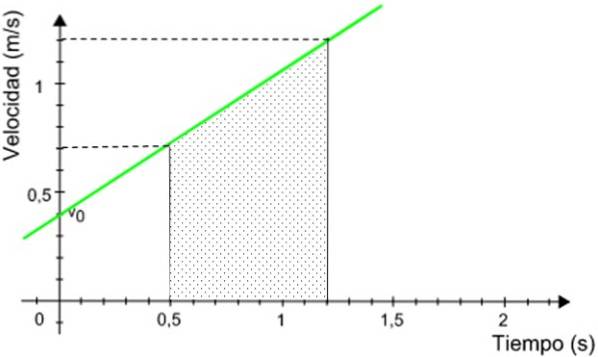
Het gearceerde gebied is het gebied van een rechter trapezium, gegeven door:
A = (Grote sokkel + kleine sokkel) x hoogte / 2
EEN = (1,2 + 0,7) m / s x (1,2 - 0,5) s / 2 = 0,665 m
Referenties
- Baldor, A. 2004. Vlak- en ruimtegeometrie met trigonometrie. Culturele publicaties.
- Bedford, A. 1996. Statics. Addison Wesley Interamericana.
- Jr. geometrie. 2014. Veelhoeken. Lulu Press, Inc.
- OnlineMSchool. Rechthoekige trapezium. Hersteld van: es.onlinemschool.com.
- Automatische probleemoplosser voor geometrie. De trapeze. Hersteld van: scuolaelettrica.it
- Wikipedia. Trapezium (geometrie). Hersteld van: es.wikipedia.org.



Niemand heeft nog op dit artikel gereageerd.