
Resulterende vectorberekening, voorbeelden, oefeningen
De resulterende vector is degene die is verkregen door middel van een bewerking met vectoren waarvan het resultaat ook een vector is. Normaal gesproken is deze bewerking de som van twee of meer vectoren, waarmee een vector wordt verkregen waarvan het effect equivalent is.
Op deze manier worden vectoren zoals de resulterende snelheid, versnelling of kracht verkregen. Bijvoorbeeld wanneer meerdere krachten op een lichaam inwerken F.1, F.twee, F.3,de vectorsom van al deze krachten is gelijk aan de netto kracht (de resulterende), die wiskundig als volgt wordt uitgedrukt:
F.1 + F.twee + F.3 + F.R of F.N

De resulterende vector, of het nu krachten is of een andere vectorgrootte, wordt gevonden door de regels van vectoroptelling toe te passen. Aangezien de vectoren naast een numerieke waarde ook richting en betekenis hebben, is het niet voldoende om de modules toe te voegen om de resulterende vector te hebben.
Dit is alleen waar in het geval dat de betrokken vectoren in dezelfde richting zijn (zie voorbeelden). Anders is het nodig om vectorsom-methoden te gebruiken, die, afhankelijk van het geval, geometrisch of analytisch kunnen zijn..
Artikel index
- 1 Voorbeelden
- 1.1 Geometrische methoden om twee vectoren toe te voegen
- 2 oefeningen
- 2.1 -Oefening 1
- 2.2 Oefening 2
- 3 referenties
Voorbeelden
De geometrische methoden om de resulterende vector te vinden, zijn de polygonale methode en de parallellogrammethode.
Wat analytische methoden betreft, is er de componentenmethode, waarmee de vector die het resultaat is van elk systeem van vectoren kan worden gevonden, op voorwaarde dat we zijn Cartesiaanse componenten hebben..
Geometrische methoden om twee vectoren toe te voegen
Stel dat de vectoren of Y v (We geven ze vetgedrukt aan om ze te onderscheiden van de scalairen). In figuur 2a) hebben we ze in het vliegtuig geplaatst. In figuur 2 b) is het zo overgebracht naar de vector v dat zijn oorsprong samenvalt met het einde van of. De resulterende vector gaat van de oorsprong van de eerste (of) tot het puntje van de laatste (v
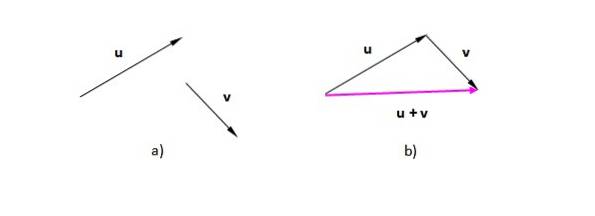
De resulterende figuur is in dit geval een driehoek (een driehoek is een driezijdige veelhoek). Als we twee vectoren in dezelfde richting hebben, is de procedure hetzelfde: plaats een van de vectoren na de andere en teken er een die van de oorsprong of staart van de eerste naar de punt of het einde van de laatste gaat..
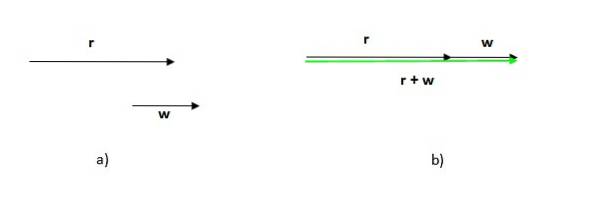
Merk op dat de volgorde waarin deze procedure wordt uitgevoerd niet uitmaakt, aangezien de som van vectoren commutatief is.
Merk ook op dat in dit geval de module (de lengte of grootte) van de resulterende vector is de som van de modules van de toegevoegde vectoren, in tegenstelling tot het vorige geval, waarin de module van de resulterende vector kleiner is dan de som van de modules van de deelnemers.
Parallellogram-methode
Deze methode is zeer geschikt als u twee vectoren moet optellen waarvan de oorsprongspunten bijvoorbeeld samenvallen met de oorsprong van een x-y-coördinatensysteem. Stel dat dit het geval is voor onze vectoren of Y v (figuur 3a):
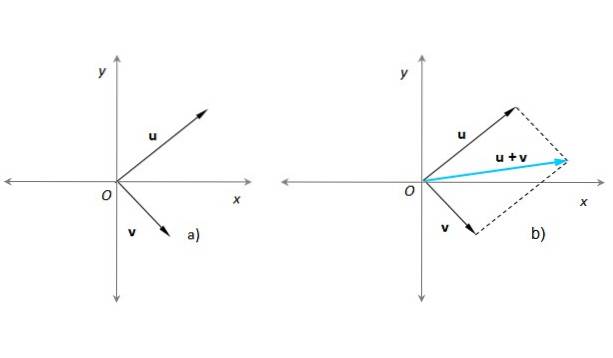
In figuur 3b) is een parallellogram geconstrueerd met behulp van stippellijnen evenwijdig aan of nu al v. De resulterende vector heeft zijn oorsprong bij O en zijn einde op het punt waar de stippellijnen elkaar kruisen. Deze procedure is volledig gelijk aan die beschreven in de vorige sectie..
Opleiding
-Oefening 1
Gegeven de volgende vectoren, zoek de resulterende vector met behulp van de traverse-methode.
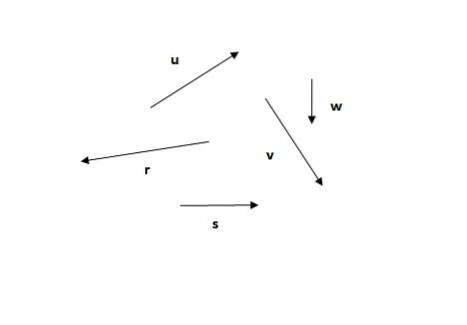
Oplossing
De traverse-methode is de eerste van de geziene methoden. Onthoud dat de som van vectoren commutatief is (de volgorde van de toevoegingen verandert de som niet), dus je kunt bijvoorbeeld beginnen met een van de vectoren of (figuur 5a) of r (figuur 5b):
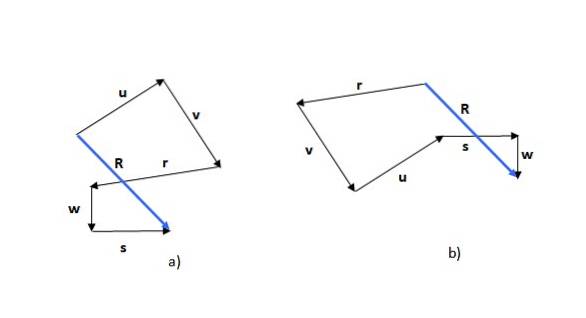
Het verkregen cijfer is een veelhoek en de resulterende vector (in blauw) wordt genoemd R. Als u met een andere vector begint, kan de vorm die wordt gevormd anders zijn, zoals te zien is in het voorbeeld, maar de resulterende vector is hetzelfde.
Oefening 2
In de volgende figuur is bekend dat de modules van de vectoren of Y v het zijn respectievelijk u = 3 willekeurige eenheden en v = 1,8 willekeurige eenheden. De hoek die of vorm met de positieve x-as is 45º, terwijl v het vormt 60º met de y-as, zoals te zien is in de figuur. Zoek de resulterende vector, grootte en richting.
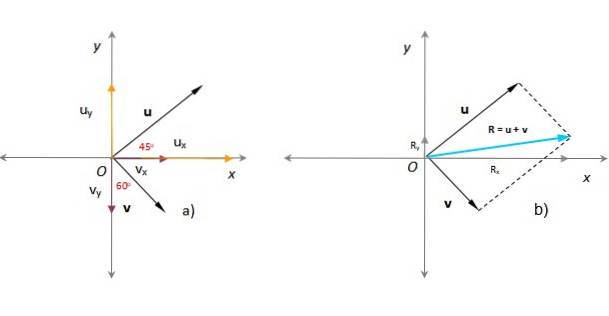
Oplossing
In de vorige sectie werd de resulterende vector gevonden door de parallellogrammethode toe te passen (in turkoois in de afbeelding).
Een gemakkelijke manier om de resulterende vector analytisch te vinden, is door de toegevoegde vectoren uit te drukken in termen van hun Cartesiaanse componenten, wat gemakkelijk is wanneer de modulus en hoek bekend zijn, zoals de vectoren in dit voorbeeld:
ofX = u. cos 45º = 3 x cos 45º = 2,12; ofY = u. sin 45º = 3x sin 45º = 2.12
vX = v. sin 60º = 1,8 x sin 60º = 1,56; vY = -v. cos 60º = -1,8 x cos 60º = - 0,9
Vectoren of Y v het zijn vectoren die tot het vlak behoren en daarom elk twee componenten hebben. Vector u bevindt zich in het eerste kwadrant en zijn componenten zijn positief, terwijl vector v zich in het vierde kwadrant bevindt; zijn x-component is positief, maar zijn projectie op de verticale as valt op de negatieve y-as.
Berekening van de cartesiaanse componenten van de resulterende vector
De resulterende vector wordt gevonden door algebraïsch de respectieve x- en y-componenten toe te voegen om hun Cartesiaanse componenten te verkrijgen:
RX = 2,12 + 1,56 = 3,68
RY = 2,12 + (-0,9) = 1,22
Zodra de cartesische componenten zijn gespecificeerd, is de vector volledig bekend. De resulterende vector kan worden uitgedrukt met de notatie tussen vierkante haken (een beugel
R = < 3.68; 1.22> willekeurige eenheden
De notatie met vierkante haken wordt gebruikt om een vector te onderscheiden van een punt in het vlak (of in de ruimte). Een andere manier om de resulterende vector analytisch uit te drukken, is door de eenheidsvectoren te gebruiken ik en j in het vliegtuig (ik, j Y k in de ruimte):
R = 3,68 ik + 1,22 j willekeurige eenheden
Omdat beide componenten van de resulterende vector positief zijn, is de vector R behoort tot het eerste kwadrant, dat al eerder grafisch was gezien.
Omvang en richting van de resulterende vector
Als we de cartesische componenten kennen, wordt de grootte van R berekend via de stelling van Pythagoras, aangezien de resulterende vector R, samen met zijn R-componentenX en RY vormen een rechthoekige driehoek:
Omvang of module: R = (3.68twee + 1,22twee½ = 3,88
Richting q met de positieve x-as als referentie: q = arctan (RY / RX) = arctg (1,22 / 3,68) = 18,3 º
Referenties
- Vectoren en regels toevoegen. Teruggeplaatst van: newt.phys.unsw.edu.au
- Figueroa, D. Series: Physics for Sciences and Engineering. Deel 1. Kinematica 31-68.
- Fysiek. Module 8: Vectoren. Hersteld van: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mechanica voor ingenieurs. Statisch. 6e editie. Continental Publishing Company. 15-53.
- Vector Toevoeging Calculator. Opgehaald van: www.1728.org


Niemand heeft nog op dit artikel gereageerd.