Twee of meer vectoren zijn teamlens als ze dezelfde module hebben, dezelfde richting en hetzelfde zintuig, zelfs als hun punt van oorsprong anders is. Onthoud dat de kenmerken van een vector precies zijn: oorsprong, module, richting en gevoel.
Vectoren worden weergegeven door een georiënteerd segment of pijl. Figuur 1 toont de weergave van verschillende vectoren in het vlak, waarvan sommige teamlensing zijn volgens de aanvankelijk gegeven definitie..
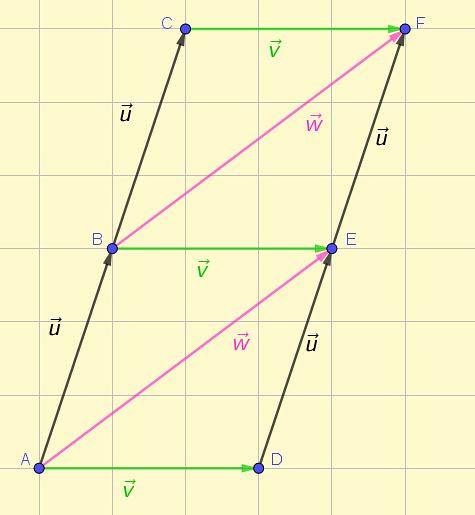
Op het eerste gezicht is het mogelijk om te zien dat de drie groene vectoren dezelfde grootte, dezelfde richting en hetzelfde gevoel hebben. Hetzelfde kan gezegd worden over de twee roze vectoren en de vier zwarte vectoren.
Veel natuurgrootten vertonen een vectorachtig gedrag, zoals snelheid, versnelling en kracht, om er maar een paar te noemen. Vandaar het belang om ze op de juiste manier te karakteriseren.
Artikel index
Om vectorgrootheden van scalaire grootheden te onderscheiden, wordt vaak het vetgedrukte lettertype of een pijl boven de letter gebruikt. Wanneer u met de hand met vectoren werkt, op de notebook, is het noodzakelijk om ze te onderscheiden met de pijl en bij gebruik van een gedrukt medium wordt vetgedrukt gebruikt.
Vectoren kunnen worden aangeduid door hun vertrek- of herkomstpunt en aankomstpunt aan te geven. Bijvoorbeeld AB, BC, VAN Y EF van figuur 1 zijn in plaats daarvan vectoren AB, BC, VAN Y EF zijn scalaire grootheden of getallen die de grootte, modulus of grootte van hun respectievelijke vectoren aangeven.
Om aan te geven dat twee vectoren teamgericht zijn, wordt het symbool ' ". Met deze notatie kunnen we in de figuur de volgende vectoren aanwijzen die teamgericht op elkaar zijn:
AB∼BC∼DE∼EF
Ze hebben allemaal dezelfde omvang, richting en betekenis. Daarom voldoen ze aan de hierboven aangegeven voorschriften..
Elk van de vectoren in de afbeelding (bijvoorbeeld AB) is representatief voor de set van alle apparatuurlens vaste vectoren. Deze oneindige set definieert de klasse van vrije vectoren of.
of AB, BC, DE, EF, ...
Een alternatieve notatie is de volgende:
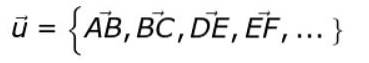
Als de vetgedrukte of de kleine pijl niet boven de letter staat of, is dat we willen verwijzen naar de vectormodule of.
Gratis vectoren worden op geen enkel punt toegepast.
Voor hun deel glijdende vectoren Het zijn teamlengtevectoren voor een bepaalde vector, maar hun toepassingspunt moet zich in de actielijn van de gegeven vector bevinden.
En de tegengestelde vectoren Het zijn vectoren die dezelfde grootte en richting hebben, maar tegengestelde zintuigen, hoewel ze in Engelse teksten de worden genoemd tegengestelde richtingen aangezien de richting ook de zin aangeeft. Tegengestelde vectoren zijn geen team.
Welke andere vectoren van die in figuur 1 zijn teamlens voor elkaar??
Afgezien van degene die al in de vorige paragraaf zijn aangegeven, blijkt uit figuur 1 dat ADVERTENTIE, WORDEN Y EC Het zijn ook teamlengtevectoren:
AD ∼ BE ∼ CE
Elk van hen is representatief voor de klasse van vrije vectoren v.
De vectoren AE Y BF
AE ∼ BF
Wie zijn vertegenwoordigers van de klas w.
Punten A, B en C bevinden zich op het cartesiaanse vlak XY en hun coördinaten zijn:
A = (- 4.1), B = (- 1.4) en C = (- 4, -3)
Zoek de coördinaten van een vierde punt D zodat de vectoren AB Y CD wees teamgericht.
Zodat CD wees teamgericht AB moet dezelfde module en hetzelfde adres hebben als AB .
De module AB kwadraat is:
AB| ^ 2 = (-1 - (-4)) ^ 2 + (4-1) ^ 2 = 9 + 9 = 18
De coördinaten van D zijn onbekend, dus we kunnen zeggen: D = (x, y)
Vervolgens: |CD| ^ 2 = (x - (- 4)) ^ 2 + (y - (-3)) ^ 2
Zoals |ABCDis een van de voorwaarden voor AB Y CD wees teamgericht, je hebt:
(x + 4) ^ 2 + (y + 3) ^ 2 = 18
Omdat we twee onbekenden hebben, is een andere vergelijking vereist, die kan worden verkregen uit de voorwaarde dat AB Y CD zijn parallel en in dezelfde zin.
De vectorhelling AB geeft uw adres aan:
Helling AB = (4-1) / (- 1 - (-4)) = 3/3 = 1
Geeft aan dat de vector AB 45º met de X-as.
De helling van CD wordt op een vergelijkbare manier berekend:
Helling CD = (y - (-3)) / (x - (- 4)) = (y + 3) / (x + 4)
Dit resultaat gelijkstellen aan de helling van AB we hebben de volgende vergelijking:
y + 3 = x + 4
Wat betekent dat y = x + 1.
Als dit resultaat in de vergelijking wordt vervangen door de gelijkheid van de modules, hebben we:
(x + 4) ^ 2 + (x + 1 + 3) ^ 2 = 18
Vereenvoudiging blijft:
2 (x + 4) ^ 2 = 18,
Wat gelijk staat aan:
(x + 4) ^ 2 = 9
Dat wil zeggen, x + 4 = 3 wat inhoudt dat x = -1. Dus de coördinaten van D zijn (-1, 0).
De componenten van de vector AB zijn (-1 - (- 4), 4-1) = (3, 3)
en de vector CD zijn (-1 - (- 4)); 0 - (- 3)) = (3, 3)
Wat betekent dat de vectoren teamgericht zijn. Als twee vectoren dezelfde Cartesiaanse componenten hebben, hebben ze dezelfde module en richting, en daarom zijn ze teamlensing..
De gratis vector of heeft magnitude 5 en richting 143.1301º.
Zoek hun Cartesiaanse componenten en bepaal de coördinaten van de punten B en C, wetende dat de vaste vectoren AB en CD teamgericht zijn voor u. De coördinaten van A zijn (0, 0) en de coördinaten van punt C zijn (-3,2).
De situatie van de oefening kan worden weergegeven door de volgende figuur:
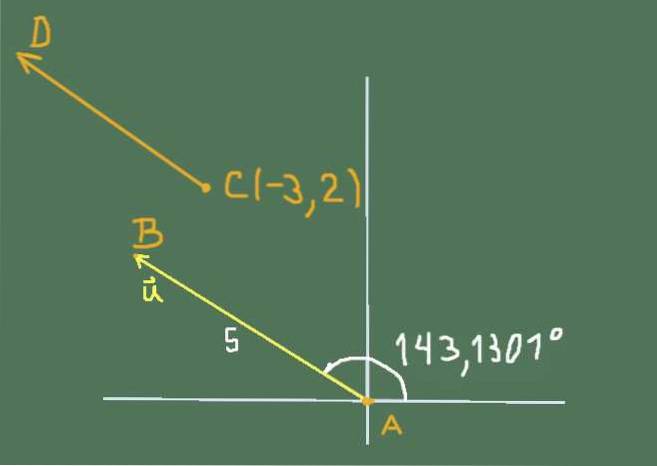
De cartesiaanse componenten van of Zij zijn
of = (5 * cos (143.1301º); 5 * sin (143.1301º))
Bij het uitvoeren van de berekeningen blijft het:
of = (-4,3)
De coördinaten van B zijn onbekend, dus plaatsen we B (x, y)
De coördinaten van de vector AB zijn (x-0; y-0), maar aangezien u teamlensing is, moet aan de gelijkheid van componenten worden voldaan, daarom volgt hieruit dat de coördinaten van B zijn (-4, 3).
Evenzo de coördinaten van de vector CD zijn (x - (- 3)); (en - 2) dat het teamgericht moet zijn u, lof leidend tot:
x + 3 = -4 en y -2 = 3
Dan zijn de coördinaten van punt D (-7, 5).
Niemand heeft nog op dit artikel gereageerd.